基于SIFT-BP的圖像配準算法
高 華,曹 鋒,陳明星
(重慶交通大學,重慶 400074)
圖像配準技術是圖像處理的重要分支,其目的是對不同時間、不同傳感器或者不同視角的2張或2張以上的圖像進行匹配。該技術廣泛應用于機器視覺、遙感圖像、醫學影像、三維重構等。圖像的配準一般采用基于區域或基于特征[1-3]。基于區域的配準方法要先比較區域內的各個像素點,然后建立圖像之間的變換模型參數,因此其計算量大,配準時間長。如果圖像存在縮放旋轉或扭曲,就會影響圖像配準的精確性,進而影響到后續工作的處理。基于特征的圖像配準方法因其配準速度快、精度高、魯棒性好而成為研究熱點。
基于特征的配準算法主要有角點匹配算法、SIFT特征[4]提取算法、SURF特征提取算法等。角點提取雖具有旋轉不變性,但是對于尺度變化較大的圖像無法保持特征的不變性;SIFT特征是圖像的局部特征,不僅對旋轉、尺度縮放、亮度變化可以保持不變性,而且對視角變化、仿射變換、噪聲也具有一定程度的穩定性[5]。
但是,傳統的SIFT算法僅考慮了特征點的描述子信息,完全忽略了特征點描述符之間的幾何信息。本文對參考圖像和映射圖像中離散的關鍵點應用BP算法,將關鍵點的相似度融入到消息傳遞過程中,以迭代算法計算對應關鍵點,不但利用了關鍵點的局部信息,而且保持了映射圖像中關鍵點間的空間約束。
1 SIFT特征檢測與匹配
1.1 特征檢測
SIFT算法特征點的檢測基于尺度空間理論。二維圖像的尺度空間定義為

其中:G(x,y,δ)是二維高斯函數;δ為尺度空間因子;(x,y)表示圖像的像素位置。
為了在尺度空間檢測到有效的關鍵點,提出用不同的高斯差分核分別與圖像進行卷積生成高斯差分尺度空間:

DoG算子計算簡單,是歸一化LoG算子的近似。
利用SIFT算法構造DOG金字塔時通過相鄰尺度空間函數相減即可。在形成的尺度空間中的3×3×3的空域和尺度域結合的鄰域里進行非最大值抑制。一個點如果在尺度空間本層以及上下26個鄰域中值是最大或最小時,才可認為是特征點。通過擬合3維2次函數精確確定特征點的位置和尺度,同時去除對比度低的特征點和不穩定的邊緣響應點。
1.2 特征點描述
1.2.1 確定特征點主方向
為了使關鍵點具備旋轉不變性,利用關鍵點鄰域像素的梯度方向的分布特性為每個關鍵點指定方向參數:以特征點為中心,在鄰域窗口內采樣,用梯度方向直方圖統計鄰域像素的梯度方向,峰值代表特征點處鄰域梯度的主方向,即為特征點的主方向,如果存在相當于主峰值80%能量的峰值時,則作為特征點的輔方向。因此,一個特征點可能會有1個主方向和1個以上的輔方向,這可以增強匹配的魯棒性。
1.2.2 構建描述子
首先將坐標軸旋轉為關鍵點的方向,以確保旋轉不變性,然后將以關鍵點為中心的8×8的窗口分成16個2×2的小塊,并計算各小塊內8個方向的梯度方向直方圖再進行累加,形成一個種子點,。每個種子點對應8個方向的向量信息,則每個關鍵點就對應16×8=128維的向量。
1.2.3 SIFT 特征向量的匹配
Lowe提出的SIFT算法采用歐式距離作為兩幅圖像間的相似性度量,即如果最近的距離除以次近的距離少于某個比例閾值,則認可該匹配點是對的。
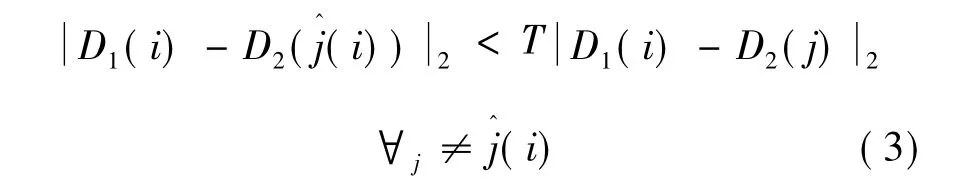
其中:D1(i)、D2(j)分別為參考圖和映射圖中的第i個和第j個特征向量;T為不依賴于圖像的常量。
1.3 改進的SIFT匹配算法
盡管SIFT算法可以提取圖像獨特的特征,但是最近歐氏距離決定了它只是一種局部優化的方法,完全忽略了不同的特征描述符之間的幾何信息。這造成的后果就是本應映射在參考圖描述符附近的映射圖描述符距離可能很遠。為此本研究作一個全局優化匹配并且定義一個補償函數φ(m),表示參考從一個關鍵點到另一個關鍵點的距離和映射圖對應關鍵點之間的距離的差異總和,如式(4)所示。
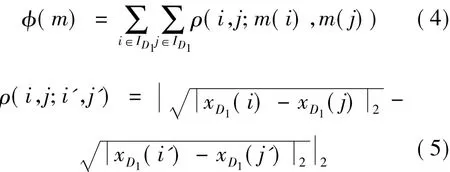
其中:ID1是原始圖像的描述符集;m(·)是映射圖中相應于參考圖的映射描述符指數。因此,可按式(6)~(8)解決全局優化問題:
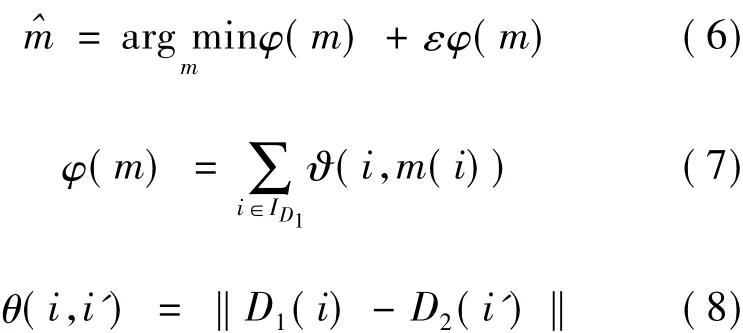
但是,式(6)不是凸函數并且帶有復雜的指數,這樣,經過式(3)計算后會丟棄一些關鍵點,但剩下的關鍵點的數量通常仍然會超過100。因此,一次徹底的搜索將需要100!步,顯然是難以計算的。此外,在這么早的階段應用式(6)也可能會不必要地丟棄有用的信息,并且式(6)有可能在存在不滿足這個條件下的匹配的情況下出現錯誤。
為此,本文提出使用信任度擴散算法(belief propagation)[7]解決式(6)出現的問題。BP算法廣泛地應用于信號處理應用中[8-9],它的優點就是目標函數的凹凸性不受限制,其主要思想是消息的迭代傳輸。首先,將整個優化問題分解成若干較簡單的局部問題。在每次迭代過程中,每個局部問題嘗試估計下一個將要進行的優化問題的最優解。相鄰的2個局部優化問題將交換信任度。每一個局部優化問題的信任度將會納入下一次迭代計算信任度的過程中。當進行到一個固定的預定義的迭代數量或者所有的局部優化問題在收斂在一個最有可能的解時,算法停止。
由于即使提出的目標函數呈指數增長,優化問題也不會發生改變,因此式(6)可改為
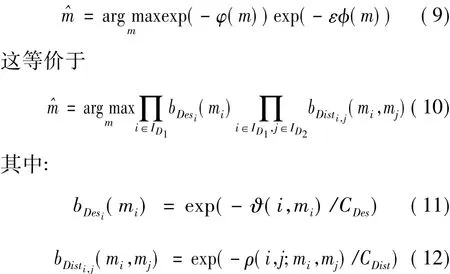
并且 CDes/CDist= ε。bDesi(mi)和 bDisti,j(mi,mj)可以分別近似看作映射圖中給定的第mi個關鍵點的描述符信息所匹配的參考圖中第i個關鍵點的信任度和第mj個關鍵點相匹配的第j個關鍵點的信息。
此時本文的優化問題轉化為式(10),但是,它并沒有使優化問題變得更易于處理。因此,把優化問題簡化一點,對于相互接近的關鍵點,使優化函數只包含 bDisti,j,在鄰域(假設 j∈N(i) ?ID1,并且,優化問題可以近似使用最大積BP 算法[10]解決。此時,
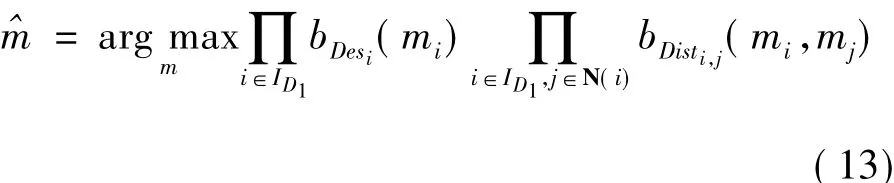
如果網絡圖是一棵樹,最大積BP算法收斂到全局最優。在一般情況下,該算法不是最理想的,但是在許多應用中卻依然工作良好[9]。定義為關鍵點i的信任度,關鍵點j在第n次迭代的正確匹配為mj。在每次迭代過程中,消息從關鍵點i傳輸到關鍵點j。改進算法描述如下:
2)當 i∈ID1時,利用式(14)迭代更新消息
3)計算每個節點的信任度:
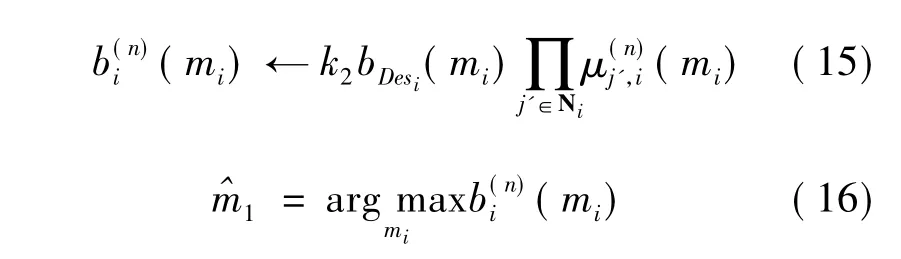
4)令n=n+1,轉至步驟2)。當n達到最大迭代次數時,算法結束。
1.4 求解圖像間的投影變換關系
假設2幅圖像滿足以下投影變換關系
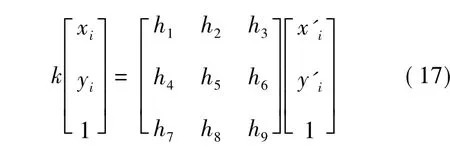
表示成向量形式為kXi=HX'i,單應性矩陣H的自由度為8,因此需要4對匹配點就可計算出H。
2 實驗分析
本文實驗操作系統為Window XP,內存為2G,編程環境是Visual 2008,OpenCV2.1。選取圖1作為待配準的原始圖像,分別用Lowe的傳統SIFT配準算法和本文的改進算法對圖1進行配準,配準結果如圖2所示。觀察可知,在傳統配準算法中有一些匹配的錯誤,特別是原始圖像的關鍵點都相當接近,然而原SIFT匹配算法基本上忽略了這些信息并且去匹配了遠離該關鍵點的其他關鍵點中的一個,本文提出的BP算法卻試圖保持關鍵點的距離不變。在傳統算法中,上下圖像分別包含了306279個特征點,有效匹配點對數為65。使用改進的匹配算法后,上下圖像分別提取了284252個特征點,有效匹配點對數為78。可見與傳統算法相比,改進的算法提高了提取特征點位置的精確度與匹配的準確性。本文CDes被設置成40000,CDist設置為 550。



圖3 改進算法配準效果
3 結束語
本文實現了基于BP的SIFT特征點的改進的圖像配準算法。在圖像配準的過程中,對于傳統SIFT算法忽略特征點的位置信息等,提出了利用信任度擴散算法求解關鍵點之間的匹配關系,將關鍵點的相似度融入到消息傳遞過程中,以迭代的方法計算對應點,最后利用投影變換矩陣對之進行匹配。在配準的過程中,改進算法比傳統的方法有了顯著的改善,不但減少了誤匹配點,降低了誤匹配率,而且與原始算法相比,能夠找出更多的匹配點,增強了定位的魯棒性。
[1]趙向陽,杜利民.一種全自動穩健的圖像拼接融合算法[J].中國圖象圖形學報,2004,9(4):417 -422.
[2]關曉菊,周激流,何坤.基于方向能量的灰度圖像邊緣檢測[J].激光雜志,2010,31(2):14 -16.
[3]范永輝,王剛,曲文娟.基于小波域分類隱馬爾可夫樹模型的圖像融合算法研究[J].激光雜志,2009,30(5):32-34.
[4]Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91 -110.
[5]YANG HENG,WANG QING.A novel local feature descriptor for image matching[Z]//IEEE International Conference on Multimedia and Expo.[S.l.]:[s.n.],2008:1405-1408.
[6]Fischler M A,Bolles R C.Random Sample Consensus:A Paradigm for Model Fitting with Applications to Image A-nalysis and Automated Cartography[J].Communications of ACM,1981,24(6):381 -395.
[7]Pearl J.Probabilistic reasoning in intelligent systems:networks of plausible inference[M].San Francisco:Morgan Kau Fmann Publishers Inc,1988.
[8]Kschischang F,Frey B,Loeliger H.Factor graphs and the sum-product algorithm[J].IEEE Trans Inform Theory,2001,47:498 -519.
[9]Sun J,Zheng N N,Shum H Y.Stereo matching using belief propagation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(7):787 -800.
[10]MacKay D.Information Theory,Inference,and Learning Algorithms[M].Cambridge:[s.n.],2003.

