多級穿廊結構坑道口部內爆炸沖擊波傳播規律的實驗研究＊

王啟睿，張曉忠，孔福利，張福明

（總參工程兵科研三所，河南 洛陽 471023）

近幾場局部戰爭表明，在坑道口部內發生爆炸已成為可能。由于內爆炸產生的強沖擊波具有峰值壓力大、持續時間長、并將引起防護門后次生沖擊波的特點，因此，它將對包括防護門在內的結構、設備和人員等均構成極大威脅。近年來，坑道口部內爆炸效應問題已引起高度關注。

穿廊結構是防護工程口部設置較典型的一種，該結構以其特有構型，通過穿廊與主坑道的T型轉折能顯著降低沖擊波峰值壓力。多次T型轉折構成的多級穿廊結構，目前已被應用在坑道工程建設中，是網絡式復雜坑道系統的基本構成部分［1－6］。隨著武器性能和坑道工程建設的快速發展，現有成果已很難滿足需求，而且，對整體功能更先進的網絡化結構形式坑道及其基本結構單元——多級穿廊結構坑道的內爆炸沖擊波效應的研究還不夠，因此，積極開展對多級穿廊結構以及網絡式復雜坑道系統機理研究，特別是實驗研究十分必要。

本文中對多級穿廊結構中內爆炸效應進行系統的實驗研究，給出多級穿廊結構中沖擊波傳播特性和峰值壓力衰減規律，擬為地下工程建設部門提供一定的理論和實驗依據。

1 實 驗

典型的多級穿廊結構由多次T型轉折的坑道構成，有幾次T型轉折稱為幾級穿廊，相應的坑道段依次為一級、二級、三級穿廊段和主坑道段，其中在主坑道段設置的防護門是坑道內最重要的防護設備之一。當發生口部內爆炸時，坑道內空氣沖擊波傳播規律及門后坑道次生沖擊波產生和發展規律是本項研究的重點。穆朝民等［7］就以上問題已經開展了大量的數值模擬工作并取得了一定成果，但還需通過開展系統的實驗研究加以驗證。

實驗平臺為鏈接式坑道模型系統，該系統由爆室和多個坑道單元按不同鏈接組合構成，連接部位密封并用高強螺栓加固，根據穿廊及其端部不同開閉情況分成多種工況。爆室與坑道材質相同，內截面尺寸為0.6m×0.6m，在爆室中心（坑道口部內）采用TNT集團裝藥，裝藥量為0.6～1.2kg，在沿坑道中軸線的側壁面上布置測點，安裝空壓傳感器進行測量。

整個研究過程中，根據不同工況和裝藥量共計進行60余炮次的實驗，結構示意和及實際實驗模型如圖1所示。

2 結果分析

2.1 多級穿廊結構坑道沖擊波傳播規律

圖1 實驗模型示意圖和現場布置Fig.1 Sketch drawings of test models and photos on the site

測得的典型波形如圖2所示。對于一級穿廊結構，穿廊端部與爆室端部均封閉條件下比開口條件下的峰值壓力明顯升高，穿廊端部一端封閉時最大升高幅度接近10倍，兩端都封閉時比一端封閉時高1.5倍。這說明，若穿廊結構的1個或2個出口遭到破壞倒塌封閉時，再發生內爆炸現象，則對主坑道的破壞效應將嚴重得多，故設計時一定要考慮穿廊端部破壞的極端情況。

對于二級穿廊結構，口部全開放情況下，內爆炸空氣沖擊波經過二級穿廊段的壓力比經過一級穿廊段相應各點上的壓力小得多，僅相當于30%左右；口部全封閉情況下類似，僅相當于28%左右。2種情況下，一級穿廊段的沖擊波壓力衰減都比二級穿廊段的快得多，如圖3（a）所示。

對于三級穿廊結構發生口部內爆炸的情況也類似，口部全開放的情況下，空氣沖擊波經過二、三級穿廊段比一級穿廊段相應各點上的壓力小得多，二級僅相當于一級穿廊段相應各點上壓力的20%左右，三級僅相當于一級穿廊段相應各點上壓力的5%左右；口部全封閉情況下，二級僅相當于一級穿廊段相應各點上壓力的30%左右，三級僅相當于一級穿廊段相應各點上壓力的7%左右。2種情況下，三、二、一級穿廊段的沖擊波壓力衰減速度依次減緩，如圖3（b）所示。

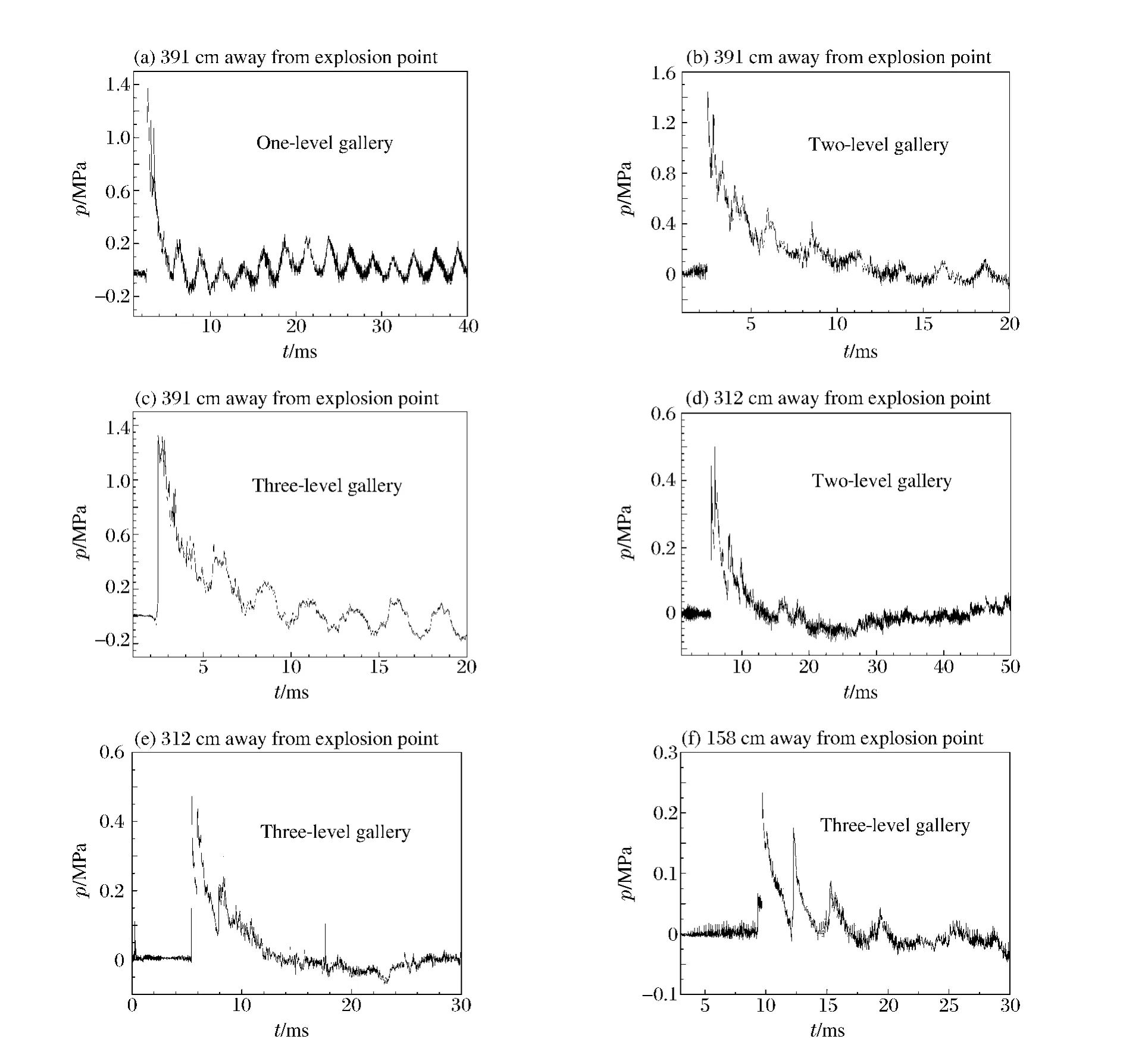
圖2 在等裝藥量、穿廊端部全開放的情況下，實驗測得的部分波形Fig.2 Tested partial waveshapes in the cases of the same charge and all ends of gallery open

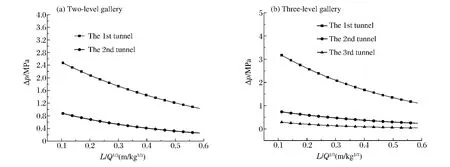
圖3 多級穿廊沖擊波衰減曲線Fig.3 Shock wave attenuation plots of multilevel gallery tunnels

根據以上分析，可將沖擊波衰減狀況按多級穿廊結構分叉的特點劃分成多個作用區段：第Ⅰ區段為一級穿廊分叉前，屬爆炸沖擊波直接作用區域，為后續結構的入射沖擊波，強度高、持續時間短；第Ⅱ區段為第Ⅰ區段后到二級穿廊分叉之間，由原入射沖擊波分成2支，一支沿一級穿廊段傳播，另一支形成二級穿廊段入射波，2段的沖擊波強度較入射波都已明顯降低；第Ⅲ區段為第Ⅱ區段后到三級穿廊分叉之間，類似第Ⅱ區段，由二級穿廊段入射波分成2支，一支沿二級穿廊段繼續傳播，另一支形成三級穿廊段入射波，沖擊波的強度降低更明顯，作用時間也相應延長；同理可推，如再有多次分級，則區段劃分及其變化規律均與此類似。沖擊波的分流過程如圖4所示，因此口部內爆炸產生的強沖擊波經過多級穿廊的分流消減，到達主坑道防護門時強度已經顯著降低，消波效果顯著。

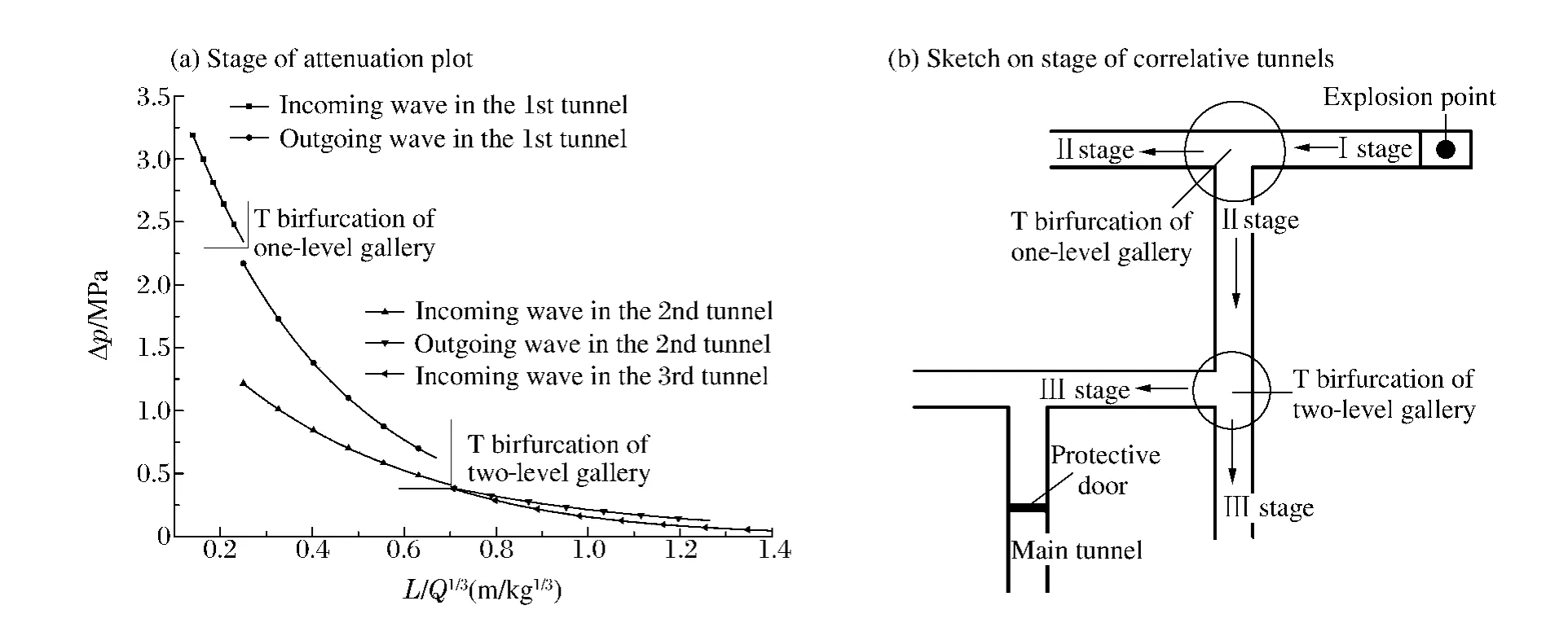
圖4 多級穿廊沖擊波衰減區段的衰減曲線和對應的坑道示意圖Fig.4 Attenuation stage of shock wave in the multi－level gallery tunnel

2.2 防護門上荷載規律

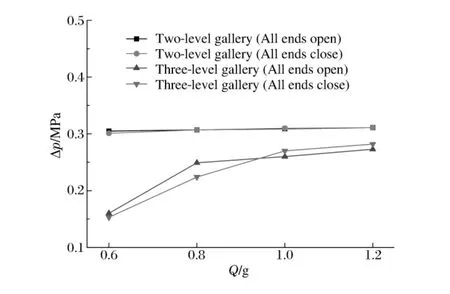
圖5 不同藥量防護門上荷載變化Fig.5 Load on the protective door under unequal charges

防護門設置于主坑道內，距離上一級穿廊結構很近，經過多級穿廊分流消減的強沖擊波到達時強度已經顯著降低，但仍有一定作用，特別是當穿廊設置較簡單或者內爆炸強度較大時，對防護門上的沖擊波荷載仍然較強。實驗結果表明：相同藥量、不同的穿廊結構之間，一級穿廊結構防護門上的壓力明顯大于二級穿廊結構，二級的明顯大于三級的；相同藥量、相同穿廊結構而不同的端口開閉情況下，整體上各端部全封閉時防護門上壓力稍大，但不同工況之間相差不很明顯。如圖5所示，二級和三級在較小藥量時壓力差值為約0.15MPa，在較大藥量時壓力差值為約0.05MPa。防護門上荷載變化也說明多級穿廊結構的顯著消波作用，如果再設置一定的防護門的防護措施，能將荷載降到更安全的范圍。

2.3 防護門后主坑道次生沖擊波的變化

坑道內強空氣沖擊波作用在防護門及門墻上時，通過高速強動力學作用引發門的振動與門后空氣的壓縮并推動壓縮波傳播，形成次生沖擊波。當振動強烈或多次振動的頻率疊加時，次生沖擊波會明顯增強，如圖6所示，次生沖擊波強度超過一定域值，亦可對人員或設備產生殺傷破壞作用。

圖6 門后次生沖擊波的形成Fig.6 Generation of secondary shock waves behind protective door

實驗研究表明，相同裝藥量情況下，三級穿廊結構主坑道防護門后次生沖擊波壓力僅相當于二級穿廊結構的36%，次生沖擊波強度較低，持續時間較長，趨于穩定。可見，三級穿廊結構與二級穿廊結構相比，對防護門后次生沖擊波強度有更好的抑制效果，如圖7所示。

2.4 與直坑道工程量比較

地下防護工程的早期設計與建筑中，主要通過長度延伸來降低沖擊波強度，即便是使用一級長穿廊結構，同時仍依靠大量增加主坑道長度等來達到有效減波目的。隨著武器的發展，單純依靠長度延伸的方法已越來越不適應現實需求，長直坑道效率較低、防護性能弱、維護投入大、容易造成空間浪費，而且施工時工程量較大，不經濟。

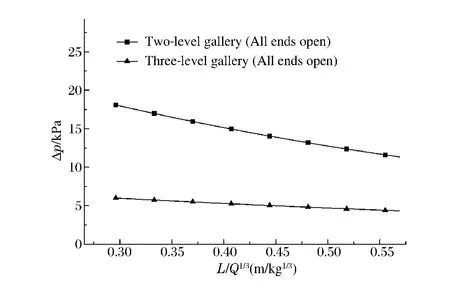
圖7 次生沖擊波變化規律Fig.7 Change of secondary shock waves

對于相同裝藥量的口部內爆炸，要達到同樣的沖擊波衰減量，則在多級穿廊結構的每一段坑道都比直坑道的長度縮短很多，如圖8所示，依次通過三級穿廊段與直接通過直坑道達到相同壓力值時，穿廊結構的比例距離僅相當于直坑道的50%左右。可見，三級穿廊結構的實際工程量相對于直坑道會大幅降低，因此，多級穿廊結構還具有顯著的經濟性。

3 結 論

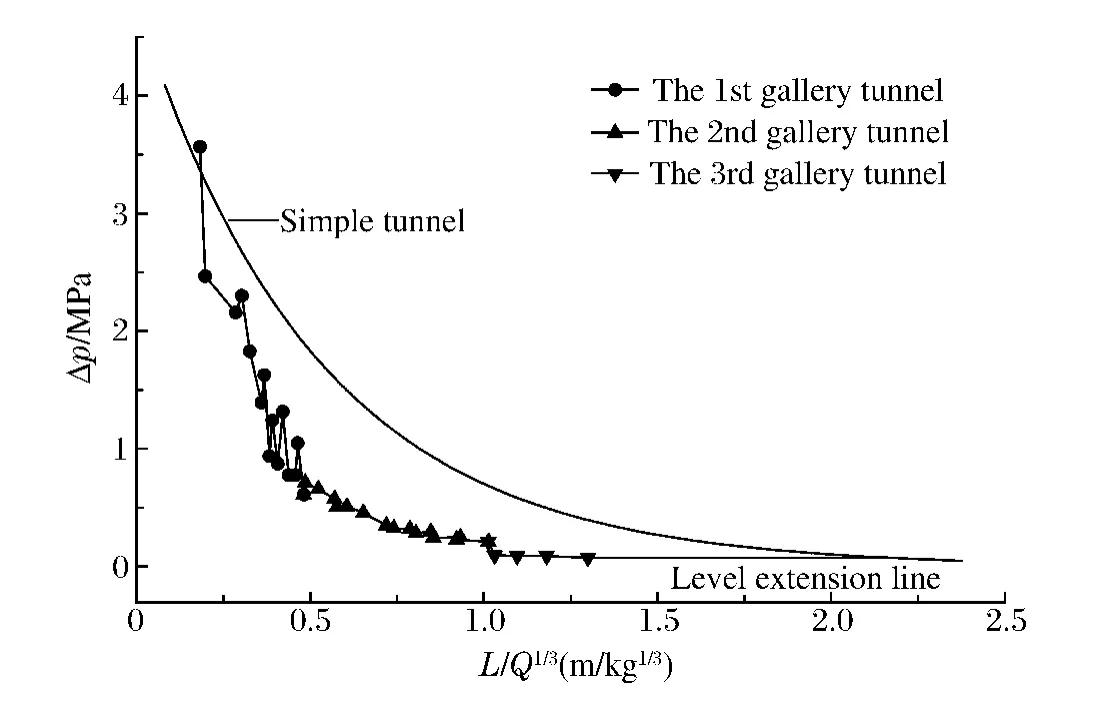
圖8 不同坑道工程量對比Fig.8 Comparison between engineers of different tunnels

（1）內爆炸情況下，穿廊結構坑道口部的開閉不同對坑道中沖擊波峰值壓力的影響很大，其中，全開放時相當于一端封閉時的60%，而一端封閉時最低僅相當于兩端全封閉時的10%。

（2）多級穿廊結構對內爆炸情況下的坑道內沖擊波峰值壓力降低效果明顯，穿廊段數越多，降低效果越顯著。口部全開放情況下，二級穿廊段的壓力僅相當于一級穿廊段相應各點的20%～30%，而三級穿廊段的壓力僅相當于一級穿廊段相應各點的5%左右；口部全封閉情況下，二級穿廊段的壓力僅相當于一級穿廊段的28%～30%，而三級穿廊段的壓力僅相當于一級穿廊段相應各點的7%左右。

（3）多級穿廊結構對降低內爆炸情況下主坑道防護門上的荷載和門后次生沖擊波強度很有利，能有效減弱對防護門及內部人員設備的毀傷效應，使結構在獲得較好防護性能的同時還能大量減少實際工程施工量，三級穿廊結構相對于直坑道達到相同沖擊波衰減幅值時，工程量減少約50%。

［1］United States Army.TM5－855－1：Fundamentals of protective design for conventional weapon［S］.1992.

［2］Atsushi A，Kazuyoshi T.Study of attenuation of shock waves propagating over arrayed spheres［C］∥Proceedings of the 24th International Congress on High－Speed Photography and Photonics.Sendai，Japan，2000：24－29.

［3］楊科之，楊秀敏.坑道內化爆沖擊波的傳播規律［J］.爆炸與沖擊，2003，23（1）：37－40.YANG Ke－zhi，YANG Xiu－min.Shock waves propagation inside tunnels［J］.Explosion and Shock Waves，2003，23（1）：37－40.

［4］龐偉賓，何翔，李茂生，等.空氣沖擊波在坑道內走時規律的實驗研究［J］.爆炸與沖擊，2003，23（6）：573－576.PANG Wei－bin，HE Xiang，LI Mao－sheng，et al.The formula for airblast time of arrival in tunnel［J］.Explosion and Shock Waves，2003，23（6）：573－576.

［5］張德良.爆炸波在復雜結構抗道內傳播的數值模擬［J］.計算力學學報，1997，14（增刊）：189－192.ZHANG De－liang.Numerical simulation on blast wave propagation in the complex tunnel［J］.Journal of Computational Mechanics，1997，14（Suppl）：189－192.

［6］李秀地，鄭穎人，李列勝.坑道中化爆沖擊波入射壓力傳播規律的研究［J］.防護工程，2005，27（3）：6－10.LI Xiu－di，ZHENG Ying－ren，LI Lie－sheng.Study on propagation law of incident shock wave pressure produced by chemical explosives in tunnel［J］.Protective Engineering，2005，27（3）：6－10.

［7］穆朝民，辛凱，任輝啟，等.爆炸沖擊波在 T形坑道內傳播規律的數值研究［J］.防護工程，2008，30（3）：32－35.MU Chao－min，XIN Kai，REN Hui－qi，et al.Numerical investigation on blast wave propagation in the T－tunnel［J］.Protective Engineering，2008，30（3）：32－35.