基于SIFT算法的異源遙感影像自動匹配研究

張建花，白仲斐，惠廣裕

（中國飛行試驗研究院 測試所，陜西 西安 710089）

光學衛星遙感成像的理論限制，難以突破云雨障礙。即使是未來研制的近地空間靜止遙感成像平臺、發射更多的遙感衛星，光學遙感也難以突破云雨氣象條件限制。面對巨型災害，如何提高航天航空遙感影像獲取的應急保障能力是一個亟待解決的問題。在瀏覽眾多云覆蓋衛星影像時，在大多情況下可以發現每一景影像總是存在或多或少的無云覆蓋區域，如果將不同傳感器、不同分辨率、不同時相、不同波段的遙感影像中無云覆蓋區域自動提取出來，然后對其進行配準并綜合生成大范圍的無云或少云覆蓋遙感影像，這就在一定程度上解決云覆蓋條件下衛星遙感影像獲取的問題，這將是提高遙感影像應急保障能力的有效途徑之一。

圖像配準技術經過多年的研究，已經取得了很多研究成果。大致可以分為2類：基于區域的配準方法和基于特征的配準方法。基于區域的配準方法利用了區域內所有像素的灰度信息，對噪聲和光照的魯棒性較差；基于特征的圖像配準方法首先提取圖像的不變特征（點、線、面），然后對這些不變特征進行匹配進而完成圖像之間的配準。然而，對于異源遙感影像來說，由于遙感影像數據量較大、影像配準的輸入數據來源的多樣性、成像條件和場景的復雜性，傳統的圖像配準技術仍然難以可靠地解決圖像特征的對應問題，多源影像自動配準問題，在遙感領域才剛剛開始。近幾年來，在計算機視覺領域，基于不變量特征描述子的方法在目標識別和圖像匹配方面取得了顯著的進展，Mikolajczyk[1]和Schmid針對不同的場景，對具有光照變化、圖像幾何變形、分辨率差異、旋轉、模糊和圖像壓縮等6種情況，就多種最具代表性的描述子（如 SIFT、矩不變量、互相關等10種描述子）進行了實驗和性能比較，結果表明SIFT描述子的性能最好。

目前，國內研究將SIFT方法用于遙感圖像配準的研究很少。本文將SIFT方法引進到具有光譜特征、空間特征、紋理特征差異的異源遙感影像自動配準技術中，并對SIFT的匹配策略進行優化，提高其可匹配性。

1 SIFT特征及匹配具體算法

SIFT[2]（Scale Invariance Feature Transform）匹配算法是一種較優秀的匹配算法，正好滿足對異源遙感影像進行配準的要求。主要步驟如下：

1.1 特征點檢測

利用不同尺度（σ）的高斯核函數對原始圖像做卷積運算，進行尺度變換。并以不同的采樣間隔采樣，建立尺度空間[3]的高斯金字塔圖像，再將相鄰尺度的高斯圖像相減得到DOG金子塔多尺度空間圖像。對DOG尺度空間內每個點與相鄰尺度和相鄰位置的點逐個進行比較，得到的局部極值（極大值和極小值）位置即為關鍵點所處的位置和對應的尺度。然后去掉低對比度的關鍵點和不穩定的邊緣響應點得到的穩定的特征點。

1.2 SIFT特征特征向量生成

在特征點周圍所在的一個區域內，依據樣本點的梯度方向生成一個方向直方圖，將方向直方圖中的峰值作為該特征點的主方向。后續的特征點構造均以該方向為參照 ,這樣所構造的描述符具有旋轉不變性。

SIFT特征描述符的構造：對任意一個關鍵點 ,在其所在的尺度空間 (即高斯金字塔結構的某一層),取以關鍵點為中心的16×16像素大小的鄰域,再將此鄰域均勻地分為4×4個子塊，在每個子塊上計算 0，45，90，135，180，225，270，315 度這8個方向的梯度大小和梯度方向直方圖。然后對每個子塊的8個方向梯度直方圖根據位置依次排序 ,這樣就構成了一個4×4×8=128維的向量,該向量就是 SIFT特征描述符。其中，第1維對應于第一子塊的第一個梯度方向，第2維對應于第一子塊的第2個梯度方向，第9維對應于第二個子塊的第一個梯度方向，依次類推。

1.3 SIFT特征特征向量匹配

采用特征向量的歐式距離來作為兩幅圖像中關鍵點的相似性判定度量。取圖像1中的某個關鍵點，并找出其與圖像2中歐式距離最近的前兩個關鍵點，在這兩個關鍵點中，如果最近的距離與次近的距離比值少于某個閾值α，則接受這一對匹配點。通過相似性度量得到潛在匹配對，其中不可避免會 產生一些錯誤匹配，因此需要根據幾何限制和其他附加約消除錯誤匹配，提高魯棒性。我們采用RANSAC算子消除錯匹配特征點。RANSAC算法的基本思想是：在進行參數估計時，不是不加區分地對待所有可用的輸入數據，而是迭代地在輸入數據中采樣所謂的最小點集，每次采樣所得到的最小點集估計出所要確定的模型參數，同時根據一定的判斷準則來判別輸入數據中哪些是與該參數相一致的，即內點，哪些是不一致的，即外點。如此迭代一定次數后，將對應輸入數據中內點比例最高的所估計參數值以及所篩選出來的內點作為RANSAC最后解。

2 異源遙感圖像實驗

1）相同傳感器圖像配準 圖1所示，左圖像為航空影像，右圖是將其旋轉60°。其中左影像檢測到1 947個SIFT特征點，右影像檢測到1 109個SIFT特征點。圖中連線表示SIFT算法的匹配點對，一共236對匹配點。經過人工篩選匹配點對坐標文件，得到正確的匹配點為195對。得到其正確匹配率為83%。采用RANSAC估計算法得到226對匹配點，去除了10對外點。

圖1 相同傳感器遙感圖像配準Fig.1 Registration of the same source remote sensing images

2）相同傳感器，不用波段的遙感圖像配準 如圖2所示。左圖像為TM傳感器的第2波段，右圖像為第6波段圖像。由于不同波段的地物波譜反射特性不同，在圖像上表現為相同地物在不同波段的圖像上亮度值差異較大。采用SIFT方法，在左圖中，檢測到2 238個SIFT特征點，在右圖中，檢測到2 872個SIFT特征點。圖中連線表示SIFT算法的匹配點對，一共145對匹配點。經過人工篩選匹配點對坐標文件，得到正確的匹配點為111對，得到其正確匹配率為77%。采用RANSAC估計算法得到141對匹配點，去除了4對外點。

圖2 不同波段遙感圖像配準Fig.2 Registration of the multi-band remote sensing images

3）不同傳感器的圖像配準 如圖3所示，左圖是SPOT衛星全色分辨率為10 m的影像，右圖是TM 30 m分辨率的影像。兩者分辨率、成像角度不同，照度也有所變化。在左影像中檢測到了7 979個SIFT特征點，在右影像中檢測到3 666個SIFT特征點。其中共有34對匹配點對，如圖中連線所示。經過人工篩選匹配點對坐標文件，得到正確的匹配點為18對匹配點對，正確匹配率為53%。采用RANSAC估計算法得到25對匹配點，去除了9對外點。

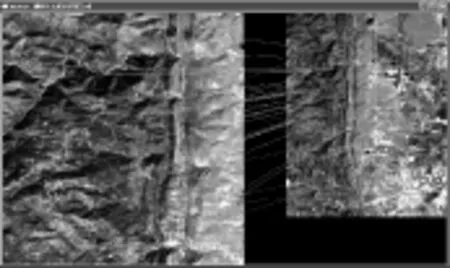
圖3 不同傳感器遙感圖像配準Fig.3 Registration of the multi-source remote sensing images

3 改進的SIFT圖像配準算法

通過以上3組實驗，表明SIFT算法對不同傳感器，不同分辨率，不同波段，不同時相的遙感圖像配準時均檢測出了大量的可匹配的特征點對。所以采用SIFT算法對異源遙感圖像配準是可行的。同時采用RANSAC估計方法剔除錯誤匹配。但是，計算SIFT特征向量時，同一個點可能有多個方向，因此屬于不同的特征點，他們中間的全部或者部分可能產生正確的匹配點對，但是實際上是同一點。因此，RANSAC算法并沒有去除這些重復匹配點對。為了更好地應用于實際，對原SIFT向量的匹配方法進行分析并改進，提出雙向匹配算法[8]。

3.1 原SIFT特征點匹配約束條件分析

設P和Q分別為兩幅圖像的特征點集，則對任一pi∈P，qj∈Q，對于相似性測度[9]S來說，如果滿足：

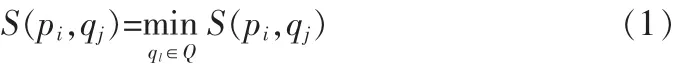
則表明qj是Q中與pi最相似的特征點。然而，如果：

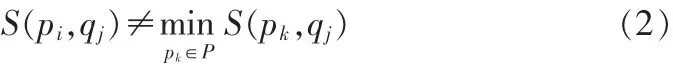
則pi不是P中與qj最相似的特征點，此時不應把 pi與qj作為對應的匹配點對。所以，對于魯棒的特征點匹配算法應該滿足如下的條件：

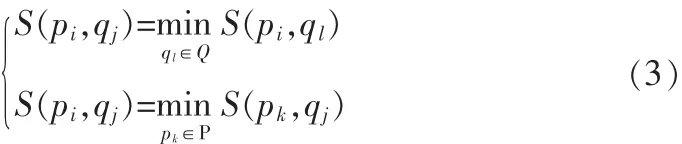
若式（3）成立，則 pi與 qj作為對應的匹配點對。反之亦然。

在D.G.Lowe的SIFT特征點初始匹配算法中，對于P中的任一特征點pi，在Q中與pi的特征向量的歐式距離最小的兩個特征點為 qj和 qj′,則對應的歐氏距離分別為 dij和 dij′，且dij≤dij′。 如果 dij＜dij′·α，則認為 pi與 qj為對應的匹配點對，其中α是一個預先設定的閾值。利用這樣的規則，可以得到兩個特征點集之間的初始匹配。

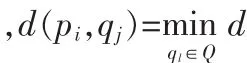
如果按照D.G.Lowe的特征點原匹配算法，就會把一些錯誤的匹配點對當作正確的匹配點對。這樣導致在初始匹配階段存在較多的錯誤匹配，而在剔除外點時，由于這些錯誤匹配對RANSAC等算法的影響，不能把所有的錯誤的匹配剔除掉。所以，最終的匹配點對中仍存在較多的錯誤匹配。因此，我們對D.G.Lowe的特征點初始匹配算法進行改進，采用雙向匹配算法。

3.2 雙相匹配算法的原理

雙向匹配算法的基本思想是根據交集思想，由原SIFT方法中的第一次匹配的結果，得到第1個特征點集在第2個特征點集中的匹配點，反過來再次求第2個特征點集中已被匹配的關鍵點在第1個特征點集中的匹配點，即求已被匹配的關鍵點在第1個特征點集中的最鄰近與次鄰近的距離比率α，α小于某個閾值的匹配點才認為是正確匹配。從而增強算法的約束條件來獲得更可靠的匹配點對。

則雙向匹配算法可表示為：

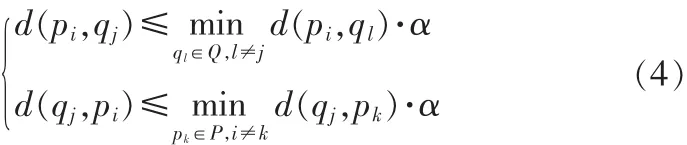
若滿足條件式（4），則認為 pi與 qj是特征匹配點對。從上面定義的條件可以看出，雙向匹配算法的約束條件都比原SIFT算法的約束條件更強。隨著約束條件的增強，一方面，在初始匹配階段，更多的外點在初始匹配階段被檢測出來，得到的初始錯誤匹配點對數減少；另一方面，在剔除外點階段，這些錯誤匹配對 RANSAC等算法的影響減弱，導致最后的總的匹配點對數和正確的匹配點對數增加，從而提高了特征點匹配的性能。實驗結果如表1所示。

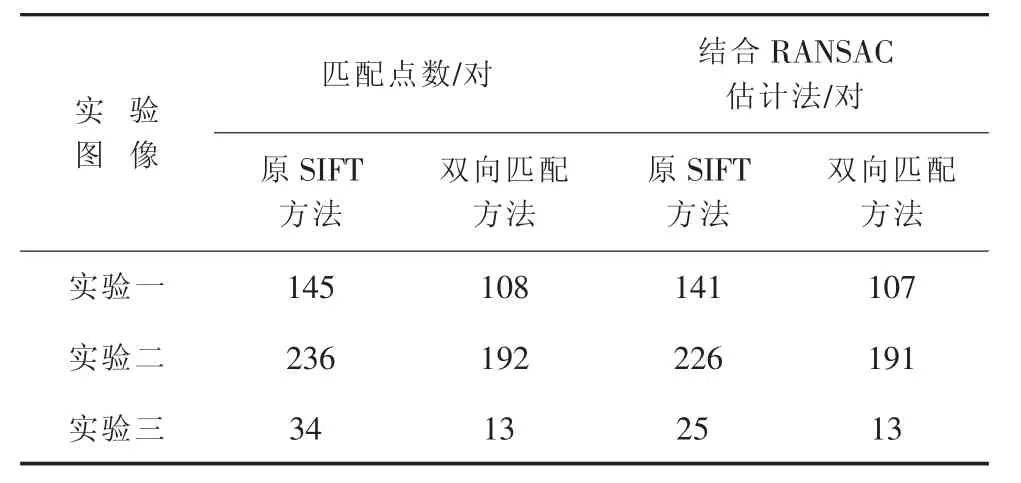
表1 雙向匹配算法的實驗結果Tab.1 The result of idirectional matching algorithm

實驗圖像與上節相同。采用RANSAC估計算法算法作為參照，實驗結果表明用雙向配算法在特征點匹配時刪除了更多的重復點對與錯誤匹配點對。驗證了我們所采用的雙向匹配方法的優越性。

4 圖像拼接結果

在Microsoft VC＋＋6.0平臺下，采用C＋＋語言編寫程序，對SIFT特征點檢測及特征向量匹配算法進行了詳細的實驗比較，并將配準后的圖像進行拼接操作，結果如圖4、5、6所示。

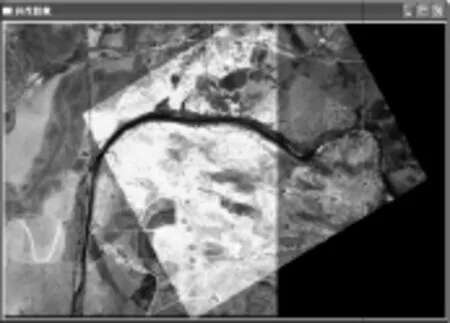
圖4 相同傳感器遙感圖像拼接結果Fig.4 Result of the same source remote sensing images

圖5 不同波段遙感圖像拼接結果Fig.5 Result of the multi-band remote sensing images

圖6 不同傳感器遙感圖像拼接結果Fig.6 Result of the multi-source remote sensing images

通過對不同傳感器、不同分辨率、不同波段、不同時相的異源遙感影像進行實驗。表明，SIFT算法簡單易行，效率較高，在圖像中可提取出大量的特征點，這些特征點對圖像的旋轉、尺度縮放、亮度變化保持不變性，對視角變化、仿射變換、噪聲也保持一定程度的穩定性；由于原SIFT方法不能去除大量重復點對和錯匹配點對，在特征向量匹配環節引入的雙向匹配算法和RANSAC估計方法可消除大量冗余的重復點對，使SIFT具有較好的魯棒性和實用性，配準結果更加準確。基于SIFT算法擴展性好，易于和其他類型特征向量聯合的特點，如果將紋理特征引入SIFT描述子的方法，應該會取得更好的匹配效果，這是下一步的研究重點。

[1]Mikolajczyk K，Schmid C.A performance evaluation of local descriptors[J].IEEE Trans on Pattern Analysis and Machine Intelligence，2005，27（10）：1615-1621.

[2]Lindeberg T.Scale-space theory：a basic tool for analysising structure s at different scales[J].Journal Applied Statistics，1994，21（2）：223-261.

[3]Lowe D G.Object recognition from local scale-invariant features[J].International Conference on Computer Vision，1990，57（4）：134-154.

[4]Lowe D.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision，2004，60（2）：91-110.

[5]Manjunath H L.A contour-based approach to multisensory image registration[J].IEEE Transactions on Image Processing，1995，4（3）：320-334.

[6]趙向陽，杜利民.一種全自動穩健的圖像拼接融合算法[J].中國圖象圖形學報，2004，9（4）：417-422.

ZHAO Xiang-yang，DU Li-min.An automatic and robust image mosaic algorithm[J].Journal of Image and Graphics，2004，9（4）：417-422.

[7]劉小軍，楊杰，孫堅偉，等.基于SIFT的圖像配準方法[J].紅外與激光工程，2008，2（1）：25-29.

LIU Xiao-Jun，YANG Jie，SUN Jian-wei，et al.Image registration approach based on SIFT[J].Infrared and Laser Engineering,2008，2（1）：25-29.