切比雪夫不等式證明的啟示及應用
楊 乾
(西南交通大學峨眉校區,四川峨眉山 614202)
切比雪夫不等式證明的啟示及應用
楊 乾
(西南交通大學峨眉校區,四川峨眉山 614202)
通過對切比雪夫不等式的證明,得到含數學期望和方差的概率不等式的證法。闡述了切比雪夫不等式是證明切比雪夫大數定律的重要工具和理論基礎,在概率論及其實際生活中有很多應用。
切比雪夫不等式;數學期望;方差
一、啟示:含有期望和方差的概率不等式的證法
定理:(切比雪夫不等式)設隨機變量X具有數學期望E(X)=μ,方差D(X)=σ2,則對任意的正數ε,有
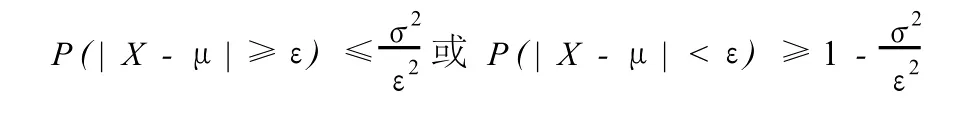
證:設X為連續性隨機變量,概率密度為f(x),則
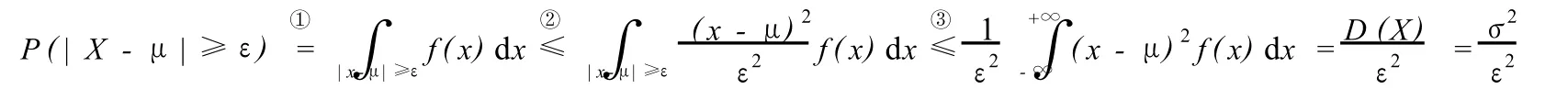
切比雪夫不等式的證明步驟:
1)先將隨機變量在區間內取值的概率用其概率密度在該區間上的積分表示;
2)利用隨機變量取值滿足的不等式,將被積函數擴大,產生概率不等式;
3)將積分區間擴大到(-∞,+∞),將積分再次擴大,切使積分化為隨機變量或隨機變量的函數的期望或方差的表達式,則得要證的概率不等式。
從中我們得到含期望和方差的概率不等式的證法。
二、切比雪夫不等式的應用
切比雪夫不等式主要有2個方面的應用:
1)利用切比雪夫不等式估計隨機變量X落入區間(a,b)內的概率P(aXb),關鍵是將待估概率P(aXb)化為的形式,方法是將不等式aXb的各端同減去E(X)
解:第一步:求E(X)和D(X)
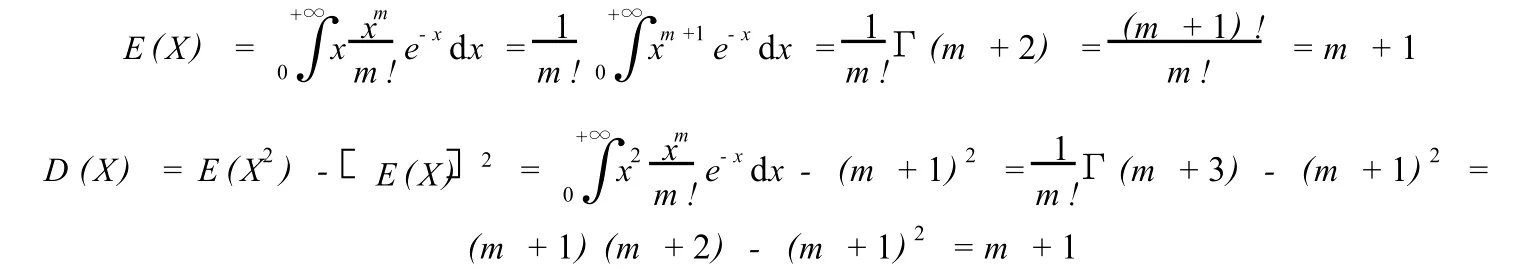
第二步:將不等式0X2(m+1)的各端同減去E(X)=m+1,把待估概率化成P(|X-E(X)|ε)的形式

第三步:取ε=m+1,利用切比雪夫不等式估計概率
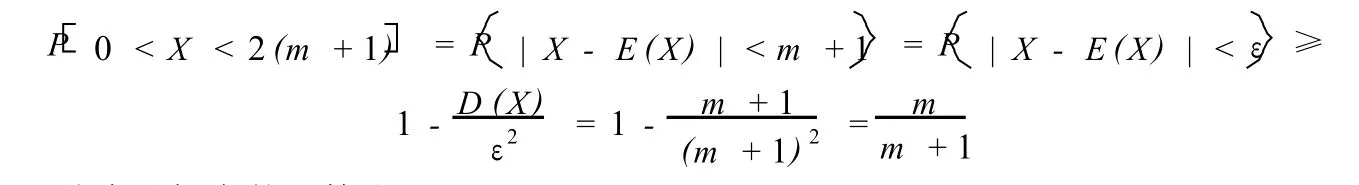
2)求解或證明一些有關概率的不等式
例2 設在每次試驗中,事件A發生的概率為0.75,利用切比雪夫不等式求:
n需要多大時,才能使得在n次獨立重復試驗中,事件A出現的頻率在0.74~0.76之間的概率至少為0.90?
解:設X為n次試驗中,事件A出現的次數,則X~B(n,0.75)
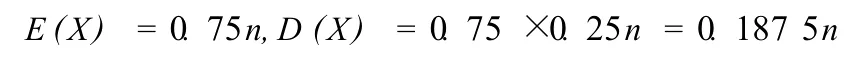
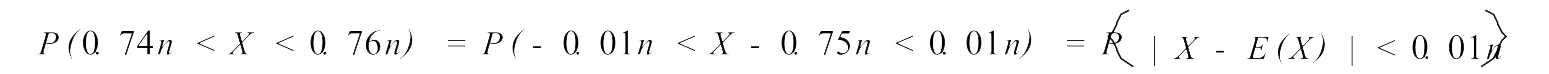
在切比雪夫不等式中取ε=0.01n,則
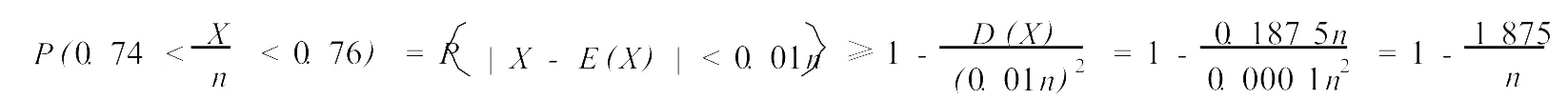
即n取18750時,可以使得在n次獨立重復試驗中,事件A出現的頻率在0.74~0.76之間的概率至少為0.90
[1]沈恒范.概率論與數理統計教程[M].4版.北京:高等教育出版社,2003.
[2]陳永華.概率論與數理統計[M].杭州:浙江大學出版社,2005.
(責任編輯周江川)
O21
A
1007-7111(2011)01-0119-02
2010-11-28
楊乾(1990—),男,研究方向:概率論與數理統計。

