隨機利率下的外匯歐式期權定價＊

吳永紅 李 瓊 金 勇

（武漢理工大學理學院 武漢 430062）

在假設兩國無風險利率為常數的情況下，利用Merton的期權定價模型可以定價外匯期權.雖然在極短的時期內，兩國的利率也許會變動極小，但不能確定完全不會變動.因此若能將兩國短期利率固定不變這一假設放寬，推導出的外匯期權定價模型會更符合實際.據此Grabbe首先提出了包含隨機利率和隨機交易匯率的模型來定價歐式貨幣期權.Hilliard，Madura和 Tucker［1］運用Vasicek的期限結構模型提高了利率分割.Amin和Jarrow［2］提出的模型對更一般的 HJM結構進行積分，進一步提高了利率分割.Amin和Bodurtha［3］通過具體的本國和外國期限結構離散時間單因子HJM模型以及匯率過程的二項式模型，考慮了Amin和Jarrow的連續時間模型，并在隨機利率下研究了美式期權的價值問題.Ekvall，Jennergren和 Naslund［4］提出了一個與以上文章相比形式更簡單的模型，其模型充分利用未保險的利率評價關系，只需要一個隨機過程即可.本文在以上文獻的基礎上，考慮了3種風險資源：本國期限結構風險，外國期限結構風險和匯率風險.在隨機利率情況下，利用鞅方法討論了外匯歐式期權的定價問題，得到了歐式看漲期權和看跌期權價格解析表達式及評價關系，并考慮了期權的對沖問題.

1 市場模型

外國折價債券價格變動的隨機過程為

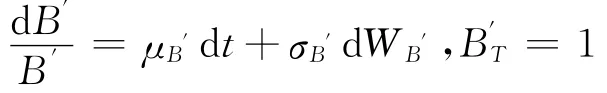
本國折價債券價格變動的隨機過程為

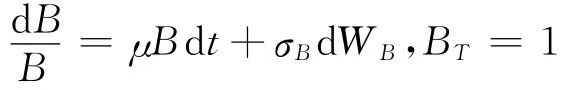
假設外匯（以本國貨幣計算）的隨機過程為

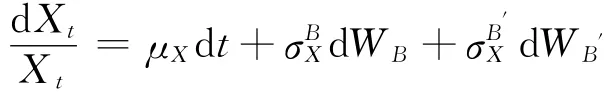
其中：μX為匯率瞬間報酬率的期望值，分別為由本國，外國利率變動引起的匯率瞬間報酬率的標準差.其中｛WB′，0≤t≤T｝，｛WB，0≤t≤T｝為概率空間｛Ω，F，P｝上標準布朗運動，令｛Ft，0≤t≤T｝為｛WB′，0≤t≤T｝，｛WB，0≤t≤T｝產生的信息流，并假定，μB，μX，σB′＞0，σB＞0，＞0＞0為可積有界非隨機函數，T為到期日.

2 期權定價公式的推導

設α（t）為國外債券數目，β（t）為國內債券數目，稱｛α（t），β（t）｝為自融資交易策略.若其財富過程Vt＝α（t）B′tXt＋β（t）Bt滿足 dVt＝α（t）×d（B′tXt）＋β（t）dBt.令 Ht＝XtB′B，代表以本國貨幣計價的外幣折價債券，則Vt＝α（t）Ht＋β（t）Bt，利用Ito引理，BHt的隨機過程可表示為

定理1 對歐式未定權益Y＝f（XT），假定f（x）為連續函數，則t時刻的無套利價格為

b）類似于a）的證明.

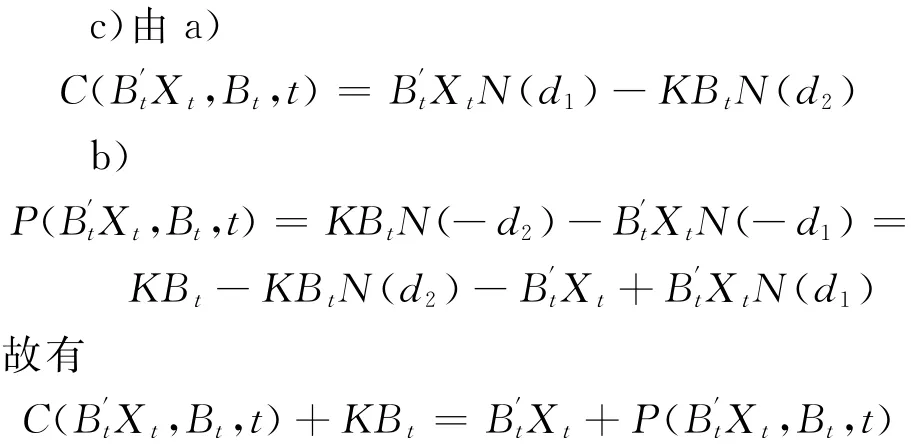
3 市場避險參數分析

從3），4），5）可以看出：外匯買權價格Ct與以本國貨幣計價的外國折價債券價格Ht，即期匯率Xt正相關，與執行價格K負相關.

對歐式看跌期權可作類似分析.

4 結 論

本文考慮了3種風險資源，在隨機利率情況下，利用鞅方法討論了外匯歐式期權的定價問題，得到了歐式看漲期權和看跌期權價格解析表達式，及評價關系，并考慮了期權的對沖問題.指出外匯買權價格與外國折價債券價格、以本國貨幣計價的外國折價債券價格，即期匯率正相關，與本國折價債券價格、執行價格負相關.考慮了本國和外國利率波動的非零相關性，本國和外國利率波動對匯率波動的影響.

［1］Hilliard J，Madura J，Tucker A，Currency option pricing with stochastic domestic and foreign interest rates［J］.Journal of Financial and Quantitative Analysis，1991，26：139－151.

［2］Amin K，Jarrow R.Pricing foreign currency options under stochastic interest rates［J］.Journal of International Money and Finance，1991（10）：310－330.

［3］Amin K I，Bodurtha J N.Discrete－time valuation of american options with stochastic interest rate［J］.Review of Financial Studies，1995（8）：193－234.

［4］Ekvall N，Jennergren P，Naslund B.Currency option pricing with mean reversion and uncovered interest parity：a revision of the garman－kohlhagen model［J］.European Journal of Operational Research，1997（10）：41－59.

［5］瑞韋茲.連續鞅與布朗運動［M］.英文版.北京：世界圖書出版公司，2008.