吉布斯自由能的多功能性質探討

張穎

(陜西師范大學化學與材料科學學院 陜西西安 710062)

按照國際純粹與應用化學聯合會(IUPAC)的定義，吉布斯能量(Gibbs energy)或吉布斯函數(Gibbs function)是焓減去熱力學溫度和熵的乘積，即G=H-TS，常稱為自由能(free energy)或自由焓(free enthalpy)。與其他熱力學函數一樣，吉布斯自由能也具有狀態函數的屬性，即其變化值ΔG只決定于系統的始態和終態，而與變化的途徑無關。Gibbs自由能具有廣泛的功能特性，如在等溫、等壓條件下可作為過程與方向的判據，還具有狹義化學勢、最大非膨脹功和狹義表面自由能等功能。

1 Gibbs自由能判據[1-2]

在等溫、等壓條件下，根據熱力學第一定律和第二定律的聯合表達式：

-δWf≤-d(U+pV-TS)或-δWf≤-d(H-TS)

可以得到-δWf≤-dG或dG≤δWf。該式的物理意義為：在等溫、等壓條件下，一個封閉系統所能做的最大非膨脹功等于其Gibbs自由能的減少。換句話說，在等溫、等壓的可逆過程中，Gibbs自由能的減少等于系統對外所做的最大非膨脹功。因此，在實際變化過程中，可通過Gibbs自由能的降低值來度量某一封閉系統能夠做有用功(即非膨脹功)的最大能力，可以表示為 dG=δWf,max或ΔG=Wf,max。

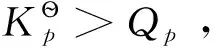
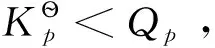
若系統在等溫、等壓且不做非膨脹功的條件下，其變化值可以表示為-ΔG≥0或ΔG≤0，即自發變化總是朝著Gibbs自由能減少的方向進行，直至平衡為止；系統不可能發生ΔG>0的變化。Gibbs自由能的變化值可作為等溫、等壓且不做非膨脹功條件下自發變化方向的判據。由于大多數反應都是在等溫、等壓條件下進行，與其他判據相比，Gibbs自由能判據更為常用。

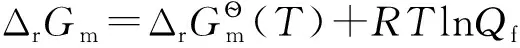
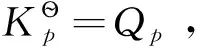
2 狹義化學勢[1-2]

在多組分系統中，每一組分的行為與各組分單獨存在時不一樣，這是由于不同種類的分子間的相互作用與同類分子間的相互作用不同。因此，在處理敞開系統或組成發生變化的封閉系統的熱力學關系時，Gibbs和Lewis引入了化學勢的概念。化學勢是宏觀物理量，它可將各組分之間的所有影響因素都包含在內。

對于一個多組分系統，其熱力學基本方程式可表示為：

dG=Vdp-SdT+μAdnA+μBdnB+…

恒定溫度和壓力條件時，dG=μAdnA+μBdnB+…

因此，Gibbs自由能具有的狹義化學勢的特性為計算ΔG提供了一條途徑。

dG=μAdnA+μBdnB=-μAdξ+μBdξ=(μB-μA)dξ

由上式可以看出，在化學反應系統中，ΔrG可以看作是反應物和生成物之間化學勢的差值。在恒定溫度和壓力條件時，可以利用反應物和生成物化學勢數值的大小來判斷反應的自發性，即當μA>μB時，ΔrG<0，即A→B正向反應自發進行；當μB>μA時，ΔrG>0，B→A逆向反應自發進行；μA=μB時，ΔrG=0，反應達平衡。

3 最大非膨脹功[1-3]

在等溫、等壓條件下，當系統發生變化時，其Gibbs自由能的減少等于對外所作的最大非膨脹功，可表示為(dG)T,p=δWf,max或(ΔrG)T,p=Wf,max。通過dG=μAdnA+μBdnB+…關系式，也可以表示為Wf,max=μAdnA+μBdnB+…。此式表明，某一系統組成的變化會產生非膨脹功。例如，在化學電池中，化學反應分別在兩個不同位置(兩個電極)發生，電功則是隨著體系中的物質由反應物變為產物而產生的。

對某一實際系統而言，若非膨脹功只有電功時，系統Gibbs自由能的減少即等于對外所作的最大電功，表示為 (ΔrG)T,p=Wf,max=-nEF。當(ΔrG)T,p<0時，電池電動勢E為正值，表明電池反應在熱力學上是自發的，即發生自發反應的電池才能做有用的電功；當(ΔrG)T,p>0時，E為負值，表明電池反應是非自發反應。

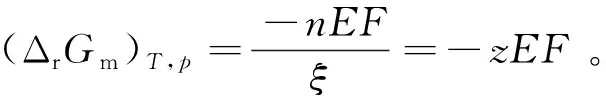
4 狹義表面自由能[2-4]

在表面物理化學的研究中，在指定各相應變量不變的情況下，每增加單位表面積時，系統熱力學能或Gibbs自由能等熱力學函數的增加值稱為廣義表面自由能，可表示為：

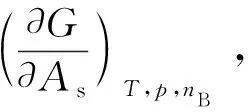
基于Gibbs自由能所具有的狹義表面自由能的性質，可以對很多實際系統進行分析。例如，在膠體分散系統中，其聚結過程是熱力學的自發過程，即ΔG<0，當表面張力γ為恒值時，ΔAs<0，即要縮小表面，只有通過聚結或聚并作用[4]。在實際系統的研究中，為獲得穩定的膠體體系，常需要加入分散穩定劑(如高分子、表面活性劑等)，在膠體表面形成表面結構層，以達到縮小表面的作用；另外，加大空間位阻，可以避免膠體粒子之間的聚結或聚并作用的發生，達到穩定膠體的目的。

選用高分子物質作為膠體系統的分散穩定劑時，當濃度和相對分子質量合適時，吸附在膠體顆粒表面的高分子物質可以降低膠體的表面能，有效避免顆粒聚集過程的發生，使膠體顆粒穩定。當高分子物質濃度較低時，不能將每個膠體顆粒包住，反而起到架橋作用，使顆粒間產生吸引作用，最終發生絮凝。因此，在很多實際體系中，如污水處理，高分子絮凝劑在加入量少時容易發生絮凝，而加入量多時可以起到保護膠體的作用。另外，利用分散制備法獲得固體分散體系時，常加入表面活性劑來穩定膠體顆粒。表面活性劑的加入，不僅能降低表面張力，而且在膠體顆粒表面形成溶劑化膜或雙層膜，達到降低膠體顆粒表面能的作用，使得膠體顆粒更穩定。

5 Gibbs自由能計算實例

與其他熱力學狀態函數一樣，ΔG數值常通過設計可逆過程進行計算，但由于Gibbs自由能特有的化學勢特性，在有些條件下也可通過化學勢的計算來獲得ΔG數值。另外，在電化學體系中，由于某些電池中進行的電極反應不易達到平衡，因而不能通過電化學實驗的方法直接測定電動勢E的準確值。可通過熱力學狀態函數計算ΔrGm，再根據熱力學與電化學之間的橋梁公式ΔrGm=-zEF得到電池電動勢E。

解法1：在等溫、等壓條件下，不可逆相變過程的ΔG常可通過設計可逆過程的方法進行計算。在已知條件充分的情況下，同一題目可設計出不同的可逆過程。

思路1：從初態出發經過3步可逆過程到達終態，即設計如圖1所示的可逆過程。

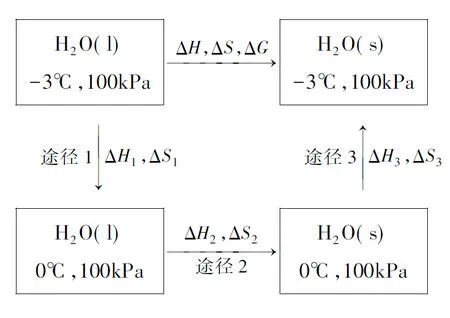
圖1可逆過程(途徑1+途徑2+途徑3)

設T1=270K，T2=273K，分別求出3步途徑中的ΔH和ΔS，即可以通過ΔG=ΔH-TΔS關系式求得ΔG。

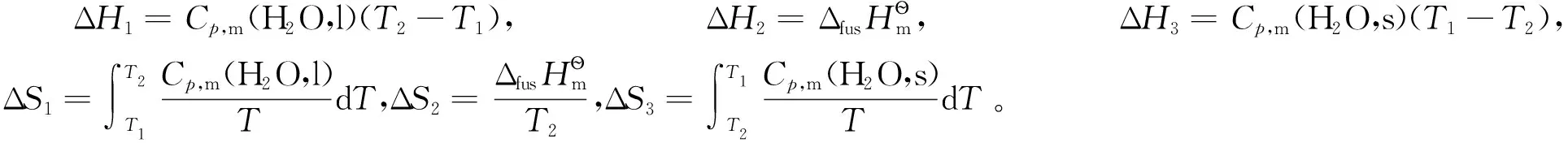
ΔH=ΔH1+ΔH2+ΔH3=-5745J，ΔS=-21.04J·K-1，ΔG=(-5745+270×21.04)J=-63.9J

思路2：假設從初態出發,經5步可逆過程到達終態，即設計圖2所示的可逆過程。

圖2可逆過程(途徑1+途徑2+途徑3+途徑4+途徑5)

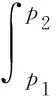
所以有：

解法2：不借助可逆途徑，利用吉布斯自由能的化學勢屬性進行計算，即分別通過初始態和終態的化學勢來計算實際變化過程的ΔG，ΔG=μ(H2O,s)-μ(H2O,l)。

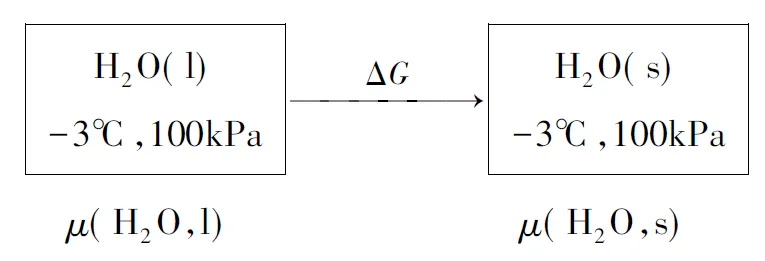
圖3狀態變化過程

設:

p1=489Pa(-3℃時水的蒸氣壓)，p2=475Pa(-3℃時冰的蒸氣壓)

其中，

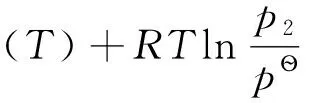
(1)

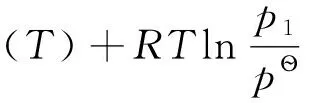
(2)

由于μ?(T)均為-3℃時的氣相純物質對應的標準態，其值相等，故(1)式減去(2)式，可得：

解法3：通過吉布斯-亥姆霍茲公式進行計算。

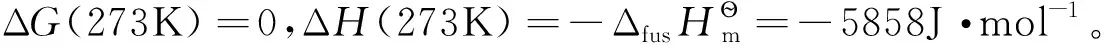
根據吉布斯-亥姆霍茲公式：

(3)

設T1=273K，T2=270K，假定由273K到270K溫度范圍內ΔH為常數，積分式(3)，得：

代入數據，計算得ΔG(270K)=-64.4J

例2[6]：已知298K時，反應2H2O(g)2H2(g)+O2(g)的平衡常數為9.7×10-81，這時H2O(l)的飽和蒸氣壓為3200Pa，試求298K時下述電池的電動勢E：

Pt|H2O(p?)|H2SO4(0.01mol·kg-1)|O2(p?)|Pt

解：反應2H2O(g)2H2(g)+O2(g)在298 K時的平衡常數是根據高溫下的數據間接計算得到的。電池中氧電極上的電極反應不易達到平衡，因此不能通過電化學方法測定電動勢E的精確值，但可通過熱力學方法計算E。

首先寫出所求電池對應的電池反應如下：

該電池是一個氫氧燃料電池，若求出該電池反應的ΔrGm，即可得到電池電動勢E。

通過設計可逆過程，將所求電池反應與題中給出了平衡常數的反應相結合，利用熱力學狀態函數的性質，可計算出電池反應的ΔrGm。

設計如圖4所示的可逆過程。

圖4可逆過程(途徑1+途徑2+途徑3)

途徑1對應的反應即題中給出的水蒸氣分解反應的逆反應。

ΔrGm,1=RTlnK?=RTln(9.7×10-81)=-456.46kJ·mol-1

途徑2是氣體的簡單狀態變化。

途徑3是飽和蒸氣壓下的氣-液兩相平衡，ΔrGm,3=0。

由此可得電池反應的ΔrGm和E。

ΔrGm=ΔrGm,1+ΔrGm,2+ΔrGm,3=(-456.46-17.06+0)kJ·mol-1=-473.52kJ·mol-1

[1] 傅獻彩,沈文霞,姚天揚,等.物理化學(上冊).第5版.北京:高等教育出版社,2006

[2] Atkins P,Paula J.Atkins′ Physical Chemistry.第7版.影印版.北京:高等教育出版社,2006

[3] 傅獻彩,沈文霞,姚天揚,等.物理化學(下冊).第5版.北京:高等教育出版社,2006

[4] 江龍.膠體化學概論.北京:科學出版社,2002

[5] 范崇正,杭瑚,蔣淮渭.物理化學-概念辨析解題方法.合肥:中國科學技術大學出版社,1999

[6] 孫德坤,沈文霞,姚天揚,等.物理化學學習指導.北京:高等教育出版社,2008