關于中心原子雜化軌道數的計算方法
蘇金昌
(大慶教育中心 黑龍江大慶 163001)
雜化軌道理論是大學化學的重要基礎理論之一,主要用來討論共價分子(或離子)的成鍵情況以及預測其幾何構型或闡述其物理化學性質。對于如何判定給定的分子(或離子)的中心原子軌道雜化方式,在雜化軌道理論里并沒有系統論述,導致在應用雜化軌道理論教與學時遇到困難。為了有利于應用雜化軌道理論闡述相關問題,本文給出一個有關中心原子雜化軌道數的計算公式,并根據計算得出的雜化軌道數確定對應的雜化軌道類型。
1 中心原子雜化軌道數的計算公式
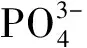
根據價鍵理論,在共價分子(或離子)中,氫原子(H)的價層一般滿足2 電子的穩定結構,而非氫原子(B)的價層一般滿足8電子的穩定結構。當每個H、B都通過一個雙電子的σ鍵與A共享2個電子時,滿足2電子穩定結構的每個H的價電子就都參與了雙電子σ鍵的形成,并沒有剩余未成鍵的價電子;而每個B的價層8個電子中除了有2個是與中心原子A共用的σ鍵電子外,還有6個是未參與雙電子σ鍵的電子,n個B共有6n個電子未參與σ鍵形成。那么,對于HmABn的V個價電子中余下的(V-6n)個價電子,如果假定它們都有在A與B、A與H之間形成雙電子σ鍵的傾向,則中心原子A傾向參與形成雙電子σ鍵的最大數為:(V-6n)/2,即V/2-3n。
假定在共價分子(或離子)中,中心原子鍵合時之所以進行軌道雜化,其主要目的是最大限度地促進中心原子與配位體之間形成更多牢固的σ鍵,即盡可能地促使σ鍵的數目傾向于最大。因為“頭碰頭” 式重疊的σ鍵越多、越牢固,構成的分子(或離子)就越穩定。可見,中心原子傾向參與形成σ鍵的最大數與其雜化軌道數之間存在著對應關系。若令G表示中心原子A的雜化軌道數,則計算中心原子雜化軌道數的公式可寫為:
G=V/2-3n
(1)
由式(1)可知,G的大小與V、n有關。即對于HmABn型分子(或離子),其中心原子(A)的雜化軌道數(G),由分子(或離子)的價電子總數(V)和非氫配位體數目(n) 決定。
用式(1)計算得出的中心原子的雜化軌道數及其雜化軌道類型、雜化軌道空間取向的對應關系歸納在表1中。

表1 中心原子雜化軌道數與雜化軌道類型及空間取向的對應關系
2 應用示例
例:次磷酸分子H2(HO)PO中P的雜化軌道數為:
G=V/2-3n=20/2-3(1+1)=4
其對應的雜化軌道類型是sp3。
應用式(1)計算了一些有代表性的分子(或離子)的雜化軌道數及對應的雜化軌道類型,其結果見表2,與有關文獻報告相符。
根據式(1)計算得出的雜化軌道數判定對應的雜化軌道類型后,再進一步結合配位數討論價鍵結構或判定共價分子(或離子)的幾何構型,可以按常規方法處理,本文不再贅述。
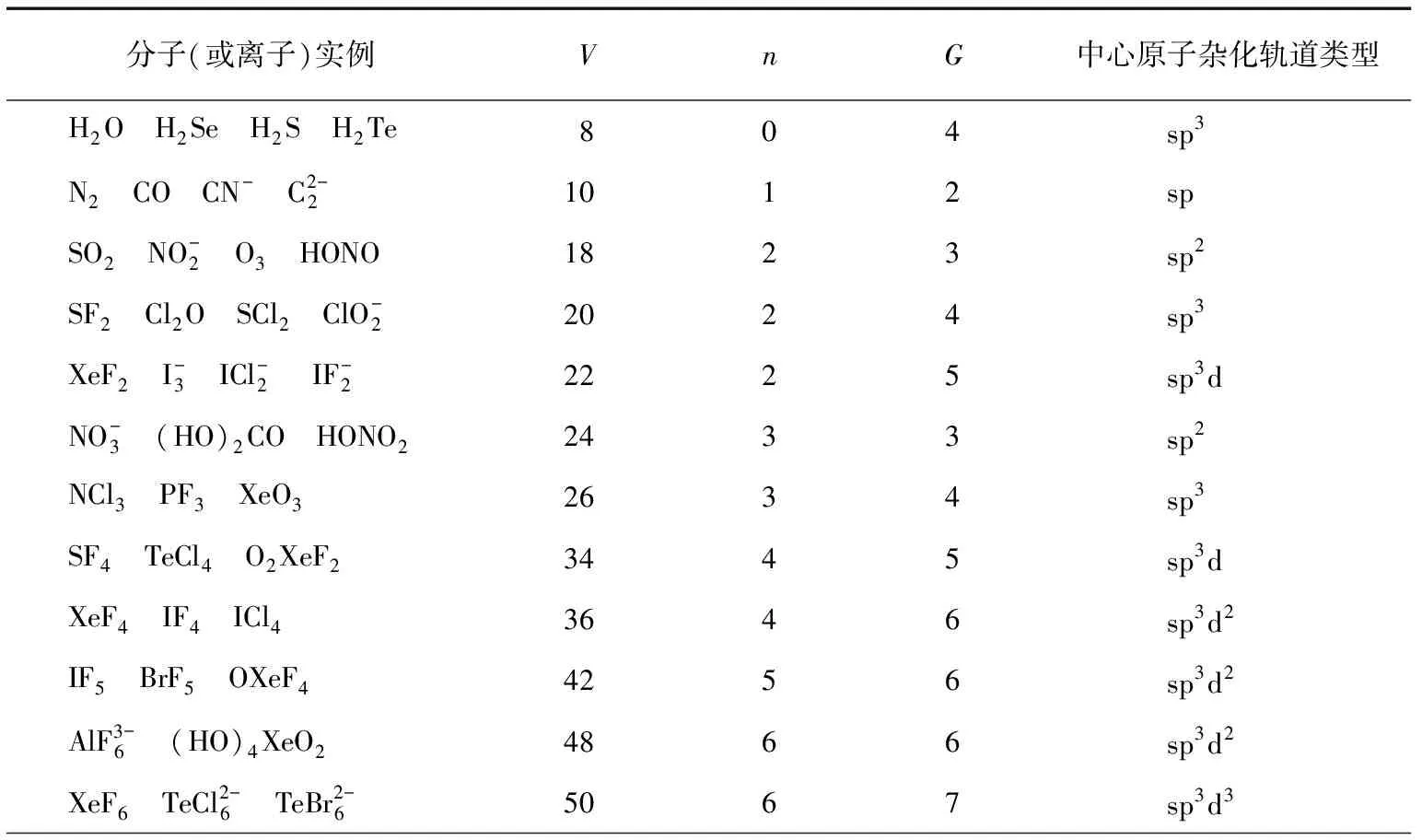
表2 代表性分子(或離子)的中心原子雜化軌道數及對應的雜化軌道類型
3 討論
1) 當m=0、n≠0時,即對于ABn型分子(或離子),式(1)的形式仍為:
G=V/2-3n
所不同的是這時的價電子總數V是1個A與n個B的價電子數之代數和。
2) 當n=0時,式(1)可簡化為:
G=V/2
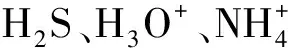
3) 對于V相同的不同分子(或離子),當n相同時,由式(1)可得出G是相同的。說明這類分子(或離子)的中心原子的雜化軌道類型是相同的,也說明“等電子分子族”結構相似性的理論依據是其中心原子軌道雜化方式的一致性。例如,表2中所列的各組實例。
4) 在分子(或離子)中,多數價電子總數V是偶數。對于少數V為奇數的分子(或離子),用(V+1)代替式(1)中的V,同樣可以得出合理的結果。
例:在價電子總數為17的NO2中,N的雜化軌道數為:
G=(V+1)/2-3n=(17+1)/2-3×2=3
其對應的雜化軌道類型是sp2。
5) 由式(1)可知,求G值并不需要先確認中心原子價層里的孤電子對,就能直接得出合理結果。這是本方法的獨特創新之處,也是諸多其他方法[1-3]所不能的。實際上,當確認了中心原子雜化軌道數及對應的雜化軌道類型,再結合配位數,其雜化軌道中有無未成鍵電子(或未成鍵電子分組情況)便一目了然。也可以用式(2)計算未成鍵的雜化軌道數,即價層中未成鍵的電子組數(L)。
L=G-(n+m)
(2)
綜上所述,應用本文提出的式(1),僅選擇2個參數(V、n)就能直接得出中心原子的雜化軌道數并確定相應的雜化軌道類型,說明該方法是一種簡單、直接、有效的方法。但需要指出的是:這種計算方法對主族元素及主族元素與零族元素形成的單中心共價分子(或離子)是有效的,而對于含有過渡金屬元素或含有多個中心原子的分子(或離子),則還有待進一步探討。
參 考 文 獻
[1] 張文廣,韋斯林,王祖浩.化學教育,2008,29(6):3
[2] 吳集貴,曾正志,姚卡玲.大學化學,1991,6(6):9
[3] 李小平.大學化學,1987,2(6):39

