定型機拉幅控制系統研究

譚寶成，曾 卉

（西安工業大學 電子信息工程學院，陜西 西安 710032）

在紡織和織造等加工過程中，對織物橫向拉幅的處理，不僅能讓織物達到需要的尺寸，還可以改善纖維網的分布結構，增加纖維沿縱向的分布。這對提高織物的拉伸強度和尺寸穩定性極為有利。拉伸率過大將產生新的高彈變形，影響最終產品的尺寸穩定性。因此，在拉幅控制過程中，最關鍵的部分就是對織物幅寬的調整，定型機拉幅部分便是在規定溫度的熱風、橫向張力作用之下對織物進行拉幅加工的部分。

拉幅控制部分的關鍵問題是對拉幅時產生的張力進行控制。張力過大，使得織物被過度牽伸，織物強度下降；張力過小，不能消除內部應力，織物尺寸也達不到要求。同時，在定型過程中，對拉幅速度也有要求，拉幅速度穩定，則張力變化的也比較平穩。如果拉幅速度過快，可能會使系統產生超調；如果拉幅速度過慢，定型時間太長。

目前大多數拉幅定型機仍采用傳統PID控制器。但傳統的PID控制器采用線性組合方法，難于協調快速性和無超調之間的矛盾，在相當多的情況下，不能取得令人滿意的效果。本系統采用變頻器和交流電機，運用矢量變頻的恒張力控制方案。利用變結構遇限削弱積分PID控制器，通過偏差大小的改變，實現了對電機實時調速的控制。

1 拉幅系統機械結構

板拉幅裝置是由設在定型機橋聯架上的拉幅器和分設在聚酯網兩側的左、右針板組成。左、右針板的基板外周設置有環形導軌梁，在導軌梁軌道上毗接排設有多個可在電機帶動下通過傳動鏈條沿導軌循環移動的針板小車，針板小車頂面上裝有雙排掛針，設置在基板內側邊各針板小車上的掛針位置均與聚酯網外側的掛針孔對位配合，在兩針板上對稱設有4個由汽缸控制的壓網裝置，前端壓網條可在汽缸控制下準確地在針板小車雙排掛針中間將網壓下。結構如圖1所示。

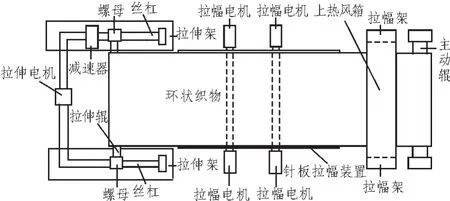
圖1 拉幅定型機示意圖Fig.1 Tentering and setting machine schemes

2 拉幅張力控制系統

定型機橫向拉幅的實現是在網子運轉的過程中，張力傳感器檢測到的張力信號傳遞給控制單元，控制單元發出控制指令，控制交流伺服電機帶動絲杠橫向往返運動，進而帶動與絲杠相連的平臺上的拉幅器橫向往返運動，實現對網子橫向張力的實時調整。

圖2為定型機的張力控制系統框圖。在實際控制模型中，由張力傳感器形成負反饋，從而構成了閉環控制系統，變頻器根據張力反饋信號進行PID運算產生一個頻率調整值，調節輸出頻率控制受控對象（異步電機），從而使輸出張力與給定的張力保持一致。

圖2 張力控制示意圖Fig.2 Tension control schemes

定型過程中，必須以恒定張力進行拉伸。主要有2個目的:一是達到預定的定型尺寸，包括幅寬和網的長度；二是使造紙網熱定型效果最佳，不會產生回縮。張力控制系統實質是控制縱向或橫幅的拉伸速度，也就是只要控制拉幅器以特定速度運行即可達到張力控制目的[1]。

3 張力系統數學模型

在拉幅定型開始之前，移動前后拉幅架使織物繃緊，并使織物橫向張力為工藝要求的初始張力。拉幅架以速度V平動拉幅。對于變形織物一般可以應用胡克定理，拉幅張力F為：

式中：ε為卷材的彈性模量；σ為卷材的截面積；L為傳動點之間的距離；t為機器啟動時間；V為拉幅線速度。

由上式可見，在織物作為張力調節對象時，是一個積分環節。控制張力實際就是在控制拉幅線速度，所以張力控制系統實際上就是一種線速度跟蹤系統。當張力達到合適張力后，應及時調整拉幅速度，這樣，織物才能在此張力下穩定運行[2]。

4 電機轉速與拉幅線速度參數間關系

拉幅電機轉動通過減速箱帶動絲杠轉動，從而對織物進行拉幅。所以電機的轉速和絲杠的轉速，即電機速度與拉幅速度之間存在著機械速比，電機的轉速很快，而絲杠的運動很慢。根據所選取的減速箱，可知道該比值。

5 電機的控制模型

異步電動機的轉速為

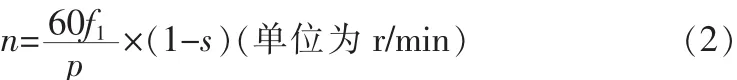
n表示旋轉磁場的轉速，p為極對數，s為轉差率。

由交流電動機的等效電路圖可以得出動態電壓方程為

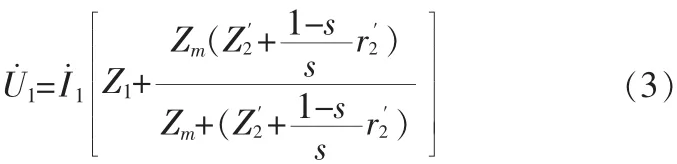
電動機旋轉運動方程為[3]：

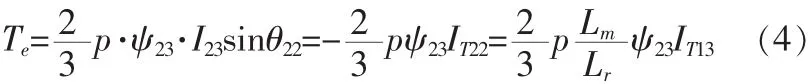
穩態時Te可簡化為：

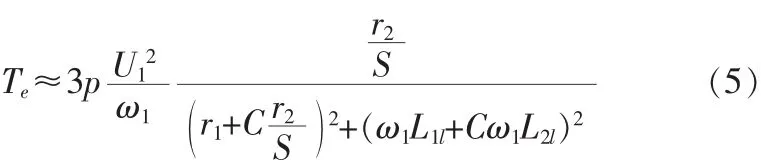
由式（1）（2）（4）得出交流電機動態結構如圖 3所示。

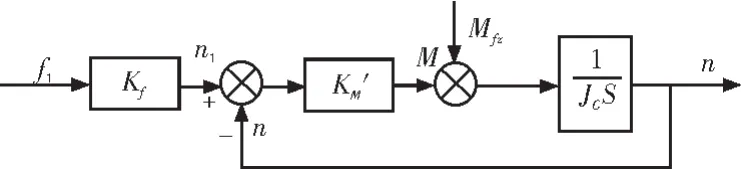
圖3 交流電機動態結構圖Fig.3 Alternating current motor dynamic structure chart

交流電機小信號時的近似傳遞函數為[4]：

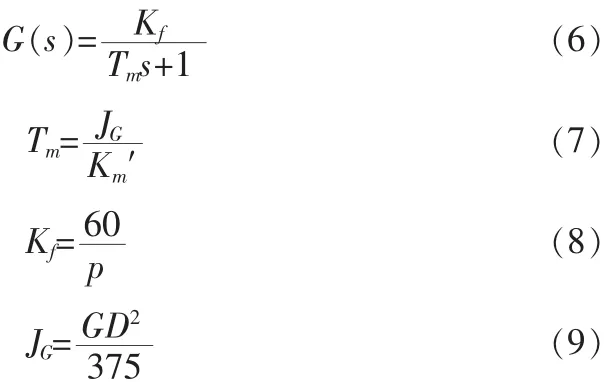
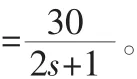
6 變結構遇限削弱積分PID算法的實現

拉幅定型的過程中，拉幅的張力不是一成不變的，當拉幅張力增大時，即電機轉速增加，為了保證定型過程的穩定性，并使電機在拉幅定型張力突然增大時能夠及時地調整其轉速，需要PLC控制臺對電機進行控制，使織物得到充分的定型。綜上所述，需要選取一種適合于該系統的控制算法，使整個輸送過程順利完成。

6.1 算法分析

實際的控制過程為：張力傳感器反饋回電機轉速信號，并轉化電機轉速偏差信號經過PID控制器以及一系列計算處理之后得到電機的電壓偏差，進而得到新的電機電壓，最后控制電機的運轉速度。

對于變化緩慢的控制對象，由于偏差較大或者累加積分項太快，將會使系統產生超調，甚至引起振蕩。其中主要原因是積分項控制不當。因此，為了消除積分飽和帶來的不利影響，采用了變結構遇限削弱積分法。這一方法是考慮了在實際過程中，控制變量U因受到執行元件機械和物理性能的約束而被控制在有限范圍內，即 Umin≤U≤Umax[5－6]。

該方法的思想是：開始運行時，將比例項加大，一旦控制變量達到設定值的70%時，將比例項減小，與此同時，當控制進入飽和區以后，便執行削弱積分項的運算而停止進行增大

積分項的運算。也就是說，在計算U（k）時，將判斷上一時刻的控制量U（k）是否已超出限制范圍，如果已超出，那么將根據偏差的符號，判斷系統輸出是否在超調區域，由此決定是否將相應偏差計入積分項。

變結構遇限削弱積分PID表達式為：

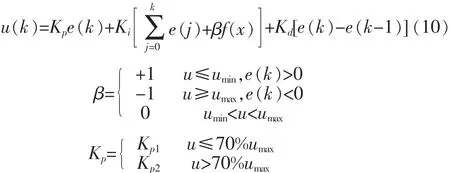
根據實際的現場情況，可以做出適合該系統的變結構遇限削弱積分法，首先為了提高系統的快速性，先增大比例項。因為實際情況下，不允許系統產生超調，所以要及時調整積分項。f（x）為一個變化的函數，當u小于限值時，積分項逐步遞增，同時調整比例項和積分項；當u大于限值時，積分項逐步遞減，同時調整比例項和積分項；當u在限值范圍內時，變化函數為0，變為普通的PID[7]。變結構遇限削弱積分算法流程如圖4所示。

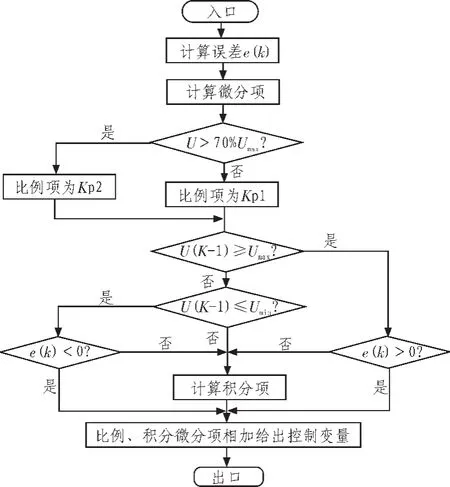
圖4 變結構遇限削弱積分算法流程圖Fig.4 Flowchartofvariablestructuremeetlimitweakenintegralalgorithm

6.2 仿真及結果分析

在不考慮負載干擾的情況下，根據7米定型機控制系統的傳遞函數，通過計算機繪制系統在不同PID控制方式下的階躍響應曲線，對該系統的動態性能進行仿真[8]，并利用狀態反饋進行校正，系統對階躍響應的曲線如圖5所示。通過仿真結果可以看出，采用文中設計的變結構遇限削弱積分PID控制可以有效地避免傳統PID控制所產生的超調[9]并提高了拉幅控制系統的快速性，其達到給定張力時間為0.98 s，而傳統的PID控制算法達到給定張力的時間為3.67 s，因此采用變結構遇限削弱積分PID控制算法，系統具有動態響應快、控制穩態性能好，并能很快趨于穩定的特點，適用于7米定型機控制系統。

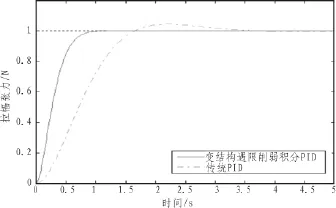
圖5 各結構PID的階躍響應對比曲線Fig.5 Step response curves of the structure PID

現場對7米定型機的拉幅張力進行了2次重復的實驗，實驗結果如表1所示。

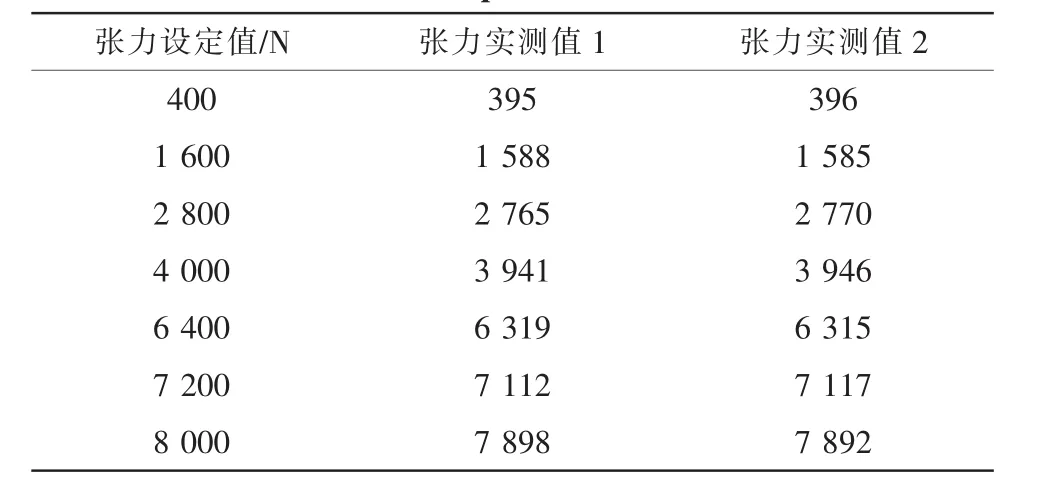
表1 實驗數據Tab.1 Experimental data

系統的允許偏差為0.02，從設定值與實際值的對比中可以看出，張力最大誤差和最小誤差值都控制在允許偏差范圍內，達到了設計的要求。因此采用文中設計的變結構遇限削弱積分PID算法來控制拉幅張力，能使其準確地停在輸入設定的張力誤差允許范圍內。

現場對7米定型的張力、速度、距離3個量進行了測量，實驗數據如表2所示。

該系統要求定型幅寬為7 m，允許偏差為0.02，根據實驗結果可以看出，定型開始時，張力為0，拉幅速度由0迅速增到1 480 r/min，然后保持恒速進行拉幅，當張力達到0.8倍給定張力，即張力為6 400 N，網的幅寬達到6.8 m時，拉幅速度開始遞減，當張力達到0.98～1倍給定張力時，即張力達到7 840～8 000 N時，認為張力已經達到了要求，拉幅速度為0，定型結束。

根據實際數據，可以看出，當定型才開始時，張力很小，隨著拉幅距離的增加，張力變化比距離變化的速度要快，當定型快達到要求時，張力迅速增加。

7 結束語

1）使用變結構遇限削弱積分PID控制算法，在定型機拉幅過程中通過調整比例、積分、微分三相參數，能及時的調整電機的轉速，提高了系統的快速啟動性能并保證了系統的控制精度。

2）通過調整積分微分的切換參數，將比例積分環節與比例微分環節相互獨立分段使用，有效地避免了拉幅過程中拉幅張力超過給定張力而產生的超調問題，即解決了張力過大對布所造成的過度牽引問題。

[1]陳靜，高殿斌，鮑振博，等.基于MATLAB的熱定型機PID張力控制器設計 [J].組合機床與自動化加工技術，2005（2）:61－62，66.

CHEN Jing，GAO Dian-bin，BAO Zhen-bo，et al.The design of tension controller of PID in the heat-setting equipment based on MATLAB [J].Combination Machine Tools and Automatic Processing Technology，2005（2）:61－62，66.

[2]郭應鋒.印刷機系統恒張力控制的研究[D].武漢:華中科技大學，2004：11－24.

[3]程偉，馬樹元，吳平東，等.交流異步電機的建模與仿真[J].計算機仿真，2005，22（3）:69－70，91.

CHENG Wei，MA Shu-yuan，WU Ping-dong，et al.Modeling and simulation of induction motor[J].Computer Simulation，2005，22（3）:69－70，91.

[4]朱銳，熱定型機的微機兩級控制系統設計[D].天津:天津工業大學，2004：28－38.

[5]畢娟，沈鳳龍.基于神經網絡的交流電機PID控制系統[J].儀表技術與傳感器，2010（2）:98－99.

BI Juan，SHEN Feng-long.AC motor PID control system based on neural network[J].Instrument Technique and Sensor，2010（2）:98－99.

[6]張曉慧.基于變結構PID的積分抗飽和控制器設計[J].黑龍江科技信息，2010（5）:43，46.

ZHANG Xiao-hui.Based on variable structure of integral PID controller design resistance to saturation[J].Heilongjiang Technical Information，2010（5）:43，46.

[7]謝維.PLC的PID自整定技術研究與實現 [J].計算機測量與控制，2009，17（8）:1544－1547.

XIE Wei.Research and implementation of PID auto-tuning technique of PLC [J].Computer Measurement&Control，2009，17（8）:1544－1547.

[8]薛定宇，陳陽泉.基于MATLAB/Simulink的系統仿真技術與應用[M].北京:清華大學出版社，2002.

[9]張蘇紅，黃韜，王進華，等.基于增量式PID控制的數控恒流源[J].現代電子技術，2011（20）:190－192，199.

ZHANG Su-hong，HUANG Tao，WANG Jin-hua，et al.Numerical control constant-current source based on incremental PID control[J].Modern Electronics Technique,2011（20）:190－192，199.