高壓管路透鏡墊連接件結構分析

閆 峰，趙宏軒，余愛英

（西安航天動力試驗技術研究所，陜西西安710100）

0 引言

液體火箭發動機由推力室、渦輪泵、燃氣發生器、閥門和調節器等組合件構成，組合件試驗成為發動機研制工作的重要組成部分。某試車臺設計用于發動機高壓組合件試驗，該試車臺的增壓系統管路和部件連接采用了透鏡墊和錐面連接的連接密封結構。擰緊力矩過大可能會導致螺栓擰斷，透鏡墊－錐面被壓碎、扭曲或斷裂，也可能使螺紋牙被剪斷而脫扣，最終影響密封質量。

本文主要通過連接結構力學分析進行了密封計算和螺栓強度校核，并在此基礎上用有限元分析軟件ANSYS對密封結構進行接觸分析，得出了透鏡墊－錐面結構在不同擰緊力矩作用下的受力狀況，為確定擰緊力矩與透鏡墊－錐面的接觸應力及接觸面積的關系及進行力學環境試驗研究提供必要的參數。

1 連接結構力學分析

在系統管路裝配過程中，透鏡墊球面和螺紋接管錐面結構在螺母擰緊力矩T的作用下，錐面和球面承受軸向預緊力F，表面之間逐漸旋合接觸壓緊，形成接觸面實現密封，連接結構如圖1所示。本文選取通徑DN65的連接結構進行結構分析和接觸分析。

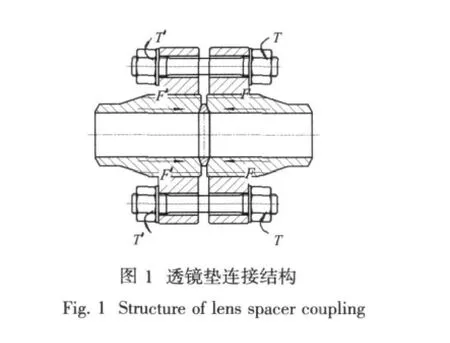
1.1 密封計算

通過比較密封面計算比壓和必須比壓，對透鏡墊連接結構進行密封計算。高壓氣體管路設計壓力為45 MPa，透鏡墊和螺紋接管材料為0Cr18Ni10Ti。

密封面上的總作用力：

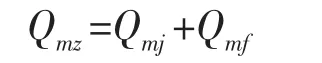
Qmj為密封面上的介質作用力：

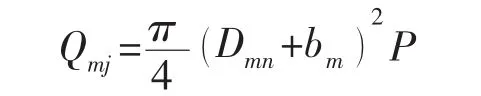
式中：Dmn為密封面內徑，Dmn＝Dk－bm，其中Dk為圓直徑，，其中，R為球半徑，θ為錐角；p為設計壓力；bm為密封面寬度，bm＝α為接觸半角，β為摩擦角，F為螺栓所受總軸向力，E為材料彈性模量。Qmf為密封面上密封力：

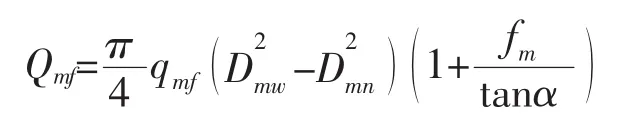
式中，Dmw為密封面外徑；Dmw=Dk+bm；qmf為密封面上必須比壓；

要保證結構密封，密封面計算比壓q應大于qmf，其中，密封面計算比壓：

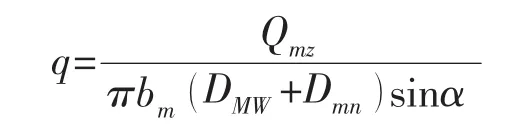
代入各參數，計算結果為：q=258 MPa＞qmf=132 MPa。因此，透鏡墊連接結構可以保證在設計壓力下的密封性。

1.2 螺栓強度校核

通過比較實際螺栓面積和需要的螺栓面積，對螺栓進行強度校核。螺栓材料：0Cr18Ni10Ti，螺母材料：2Cr13。

螺栓載荷為：

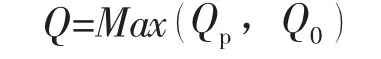
式中：Qp為工作狀態下需要的最小螺栓載荷

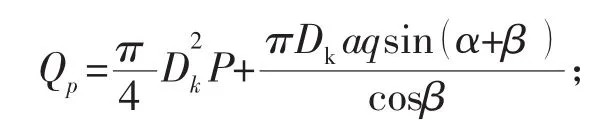
Q0為預緊狀態下需要的最小螺栓載荷

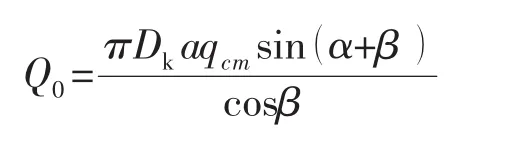
式中：qcm為預緊比壓；q為最大密封比壓；a為接觸面寬度。需要的螺栓面積：

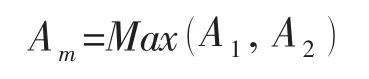
式中：A1為預緊狀態下需要的最小螺栓面積，為常溫下螺栓材料的許用應力；A2為工作狀態下需要的最小螺栓面積，為設計溫度下螺栓材料的許用應力。

要保證螺栓強度要求，應保證：實際螺栓面積A大于需要的螺栓面積上式中，A=SZ，（S為單個螺栓面積，其中d2為螺紋小徑；Z為螺栓個數）。

代入各參數，計算結果為：A=3600 mm2＞Am=2484 mm2。所選用的螺栓滿足透鏡墊連接結構在工作狀態下和預緊狀態下的強度要求。

2 透鏡墊密封數值分析

2.1 接觸分類

接觸問題是一種高度非線性行為，為了進行有效計算，必須正確理解問題的特性并建立合理的模型。接觸問題分為兩種基本類型：剛體與柔體的接觸；半柔體與柔體的接觸。在剛體與柔體的接觸問題中，接觸面的一個或多個被當作剛體，一般情況下，一種軟材料和一種硬材料接觸時，問題可以被假定為剛體與柔體的接觸，許多金屬成形問題歸為此類接觸；另一類，柔體與柔體的接觸，是一種更普遍的類型，在這種情況下，兩個接觸體都是變形體。

2.2 ANSYS接觸能力

ANSYS支持三種接觸方式：點與點，點與面，平面與面，每種接觸方式使用的接觸單元適用于某類問題。為了給接觸問題建模，首先必須認識到模型中的哪些部分可能會相互接觸，如果相互作用的其中之一是一點，模型的對應組元是一個結點。如果相互作用的其中之一是一個面，模型的對應組元是單元，例如梁單元，殼單元或實體單元，有限元模型通過指定的接觸單元來識別可能的接觸匹對，接觸單元是覆蓋在分析模型接觸面之上的一層單元。

透鏡墊密封結構是由螺紋接管錐面和透鏡墊球面構成的密封結構，屬于面與面的接觸分析。其中，螺紋接管錐面邊界作為“目標”面，而把透鏡墊球面作為“接觸”面，“目標”面總是剛性的，“接觸”面總是柔性面，這兩個面合起來作為一個“接觸對”。

2.3 接觸分析步驟

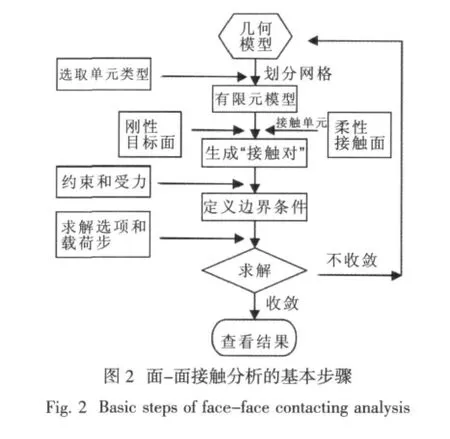
一個典型的面與面接觸分析的基本步驟如下圖所示，主要包括：

1）建立模型，劃分網格，得到有限元模型；

2）定義剛性目標面、柔性接觸面，生成“接觸對”；

3）按照約束和受力情況，定義邊界條件；

4）對接觸問題進行求解，若不能收斂，檢查模型各種設置再重新進行求解；

5）若求解收斂，則可通過后處理器或時間歷程后處理器查看位移、應力、應變，支反力和接觸信息（接觸壓力、滑動等）等計算結果。

2.4 透鏡墊密封接觸分析

對于接觸單元來說，有限元計算網格中每個單元包含應力、應變、位移等力學參數，因此可通過統計實際參加接觸的單元的位置參數得出透鏡墊－錐面密封面的實際狀態。通過求它們的接觸應力的平均值，可以得出接觸面的平均接觸應力；通過計算它們在錐面切向的密封長度可以得出密封寬度，將密封寬度乘以密封環中間段周長，可以得出整個接觸面的密封面積。

考慮到計算機的資源和運算效率，并根據透鏡墊連接件結構的幾何對稱特點，只對其中一側的密封結構進行建模，幾何模型如圖3a。其中，模型包括透鏡墊的一半，以及與其接觸的螺紋接管一個。采用ANSYS單元庫實體單元SOLID185進行網格劃分，共得到4612個節點，19308個單元。有限元模型如圖3b。

將螺紋接管錐面定義剛性目標面，透鏡墊球面定義柔性接觸面，球面-錐面構成接觸對，接觸面如圖4a所示。按照連接結構的實際工作過程，設定透鏡墊剖面為全約束，將螺栓擰緊力矩轉化為作用在螺紋接管端面的均布力，邊界條件如圖4b所示：

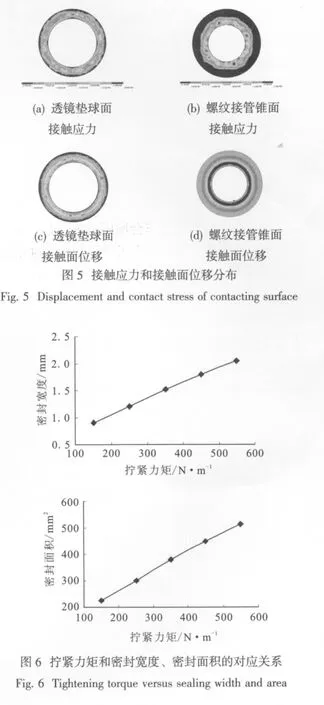
選取螺栓擰緊力矩分別為150，250，350，450和550五種工況進行了有限元計算，計算結果如表1所示。圖5a和5b給出擰緊力矩為250 N·m作用下球面和錐面等效應力分布。從圖中可以看出球面接觸點區域的最大等效應力為295 MPa，錐面接觸點區域的接觸表面最大等效應力為144 MPa。接觸面位移分布如圖5c和5d所示。

根據計算結果得出擰緊力矩和密封寬度、密封面積的對應關系如圖6所示。從這些圖中可以看出，在螺栓擰緊的過程中，密封寬度和密封面積從零開始逐漸增大，當擰緊力矩達到550 N·m時，分別達到為2.058 mm及513.22 mm2。在擰緊力矩增大過程中，球頭錐面的密封寬度和接觸面積的增長速率在逐漸減緩，變化曲線趨于平緩。

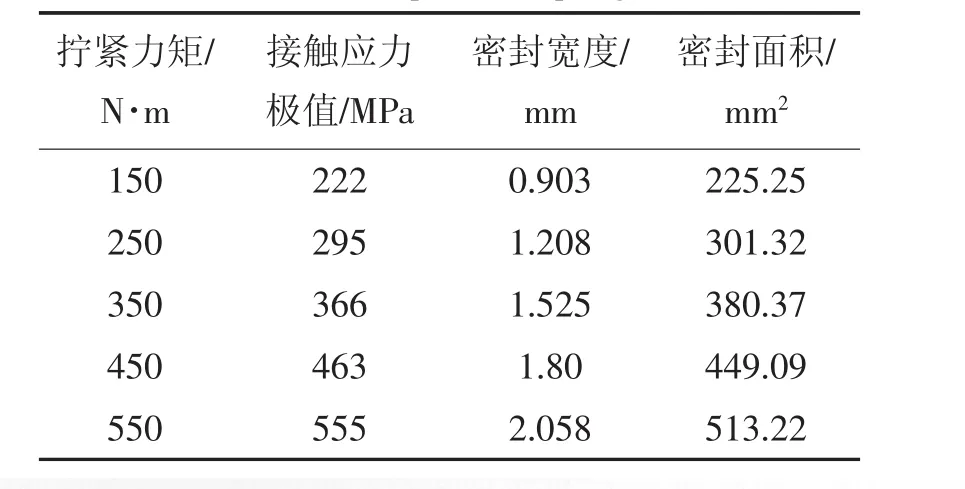
表1 透鏡墊連接件有限元數值分析結果Tab.1 Results of finite element numerical analysis for lens spacer coupling

由于在密封結構設計方法中大都將接觸應力作為密封性能的評價標準，接觸面壓力越大，密封聯接越緊密，密封性能越好。從表可看出隨著擰緊力矩的增大，平均接觸應力也逐漸增大。在550 N·m力矩作用下，球面接觸點部表面接觸應力極值高達555 MPa，已高于透鏡墊材料的極限強度，球面部分可能產生破壞。

2.5 壓力試驗

使用力矩扳手擰緊螺栓，擰緊力矩為250N·m進行了液壓強度試驗和氣密試驗。液壓強度試驗中，分為 25 MPa，35 MPa，49.5 MPa和 67.5 MPa四個壓力級別進行，每級壓力保壓10 min，無滲漏；在67.5 MPa液壓試驗中，兩法蘭間有微量變形，但泄壓后，變形回零。用45 MPa潔凈干燥的氮氣進行氣密性試驗，保壓10 min未見漏氣。

3 結論

以某高壓組合件試車臺增壓系統管路連接結構作為研究對象，進行了密封計算和螺栓強度校核。采用有限元軟件ANSYS對透鏡墊結構進行數值模擬，考察了不同預緊力下的透鏡墊結構等效應力分布和變形情況，得出了不同力矩和密封寬度、接觸面積以及接觸應力的對應關系。連接結構的液壓強度試驗和氣密性試驗表明在250 N·m擰緊力矩下，密封可靠，結構強度滿足要求。

[1]郭霄峰主編.液體火箭發動機試驗[M].北京:宇航出版社,1990.

[2]王勖成.有限單元法[M].北京:清華大學出版社,2003.

[3]陸培文.實用閥門設計手冊[M].北京:機械工業出版社,2006.

[4]博嘉科技.有限元分析軟件--ANSYS融會與貫通[M].北京:中國水利水電出版社,2002.

[5]尚曉江,邱峰,趙海峰,等.ANSYS結構有限元高級分析方法及范例應用 [M].北京:中國水利水電出版社,2006.

[6]任重.ANSYS實用分析教程 [M].北京:北京大學出版社,2003.

[7]許可,龐賀偉,孫剛.衛星推進系統管路裝配技術研究[J].航天器環境工程.2006,23(6):363-368.

[8]李珊珊,韓麗俊,梁義維.基于ANSYS的斜齒輪接觸應力有限元分析[J].機械工程與自動化.2009(4):23-24.

[9]陳署泉,肖曙紅,楊士鐵.角接觸球軸承的靜態接觸分析[J].軸承.2009(11):4-7.

[10]溫衛東,高德平.接觸問題數值分析方法的研究現狀與發展[J].南京航空航天大學學報,1994(5):664-670.

[11]劉濤,揚風鵬.精通ANSYS[M].北京:清華大學出版社,2002.

[12]郭乙木,陶偉明.線性與非線性有限元及其應用[M].北京:機械工業出版社,2003.

[13]張鑫,劉旺玉.基于ANSYS的永磁直流牽引電機接觸有限元分析[J].機械設計與制造.2010(3):27-29.

[14]肖望強,段東平,李威,等.雙壓力角非對稱齒輪輪齒接觸分析[J].農業機械學報.2010,41(8):199-205.

[15]張妍,杜四宏,袁振偉,等.齒嚙式快開門法蘭的接觸分析[J].壓力容器.2010,27(3):26-29.