一種基于耦合矩陣的新型帶通濾波器

高 山, 肖中銀, 陳文峰

(上海大學通信與信息工程學院,上海 200072)

一種基于耦合矩陣的新型帶通濾波器

高 山, 肖中銀, 陳文峰

(上海大學通信與信息工程學院,上海 200072)

提出一種新型的具有 2個傳輸零點的微帶帶通濾波器 (bandpass filter,BPF).該濾波器采用 2個新型慢波諧振器,具有較寬的上阻帶帶寬.該濾波器設計簡單,由于利用“N+2”耦合矩陣的方法而呈現出較高的頻率選擇性.測量結果表明,該濾波器具有良好的響應特性,在中心頻率 2.4 GHz處的插入損耗為 1.66 dB,上阻帶頻率達到 7.0 GHz.實測和仿真結果具有良好的一致性.

帶通濾波器;慢波諧振器;耦合矩陣;傳輸零點

本工作提出一種新型的應用于 2.4 GHz無線局域網系統的二階濾波器.2個新型慢波諧振器及其相應的饋線結構可以方便地調節外部品質系數.同時,引入源和負載之間的耦合能夠實現 2個可控的傳輸零點.由于采用了“N+2”耦合矩陣的方法,該濾波器易于設計和優化.測量與仿真結果表明,該濾波器能夠實現較高的頻率選擇性和較寬的上阻帶帶寬.

1 濾波器設計

濾波器的結構示意圖如圖 1(a)所示,該示意圖基于圖 1(b)所示的拓撲結構.根據“N+2”耦合矩陣方法和新型慢波諧振器結構分析,確定其最終優化尺寸為 L=0.6 mm,L1=1.5 mm,L2=5.2 mm,L3=8.4 mm,L4=1.7 mm,W1=0.4 mm,W2=0.6 mm,W3=1.8 mm,W4=1.2 mm,S1=1.2 mm,S2=0.4 mm,S3=0.2 mm.介質板相對介電常數為2.78,厚度為 0.8 mm.輸入、輸出饋線與諧振器之間的耦合縫隙寬度為 0.2 mm,50Ω輸入、輸出端口的寬度為 2.1 mm.

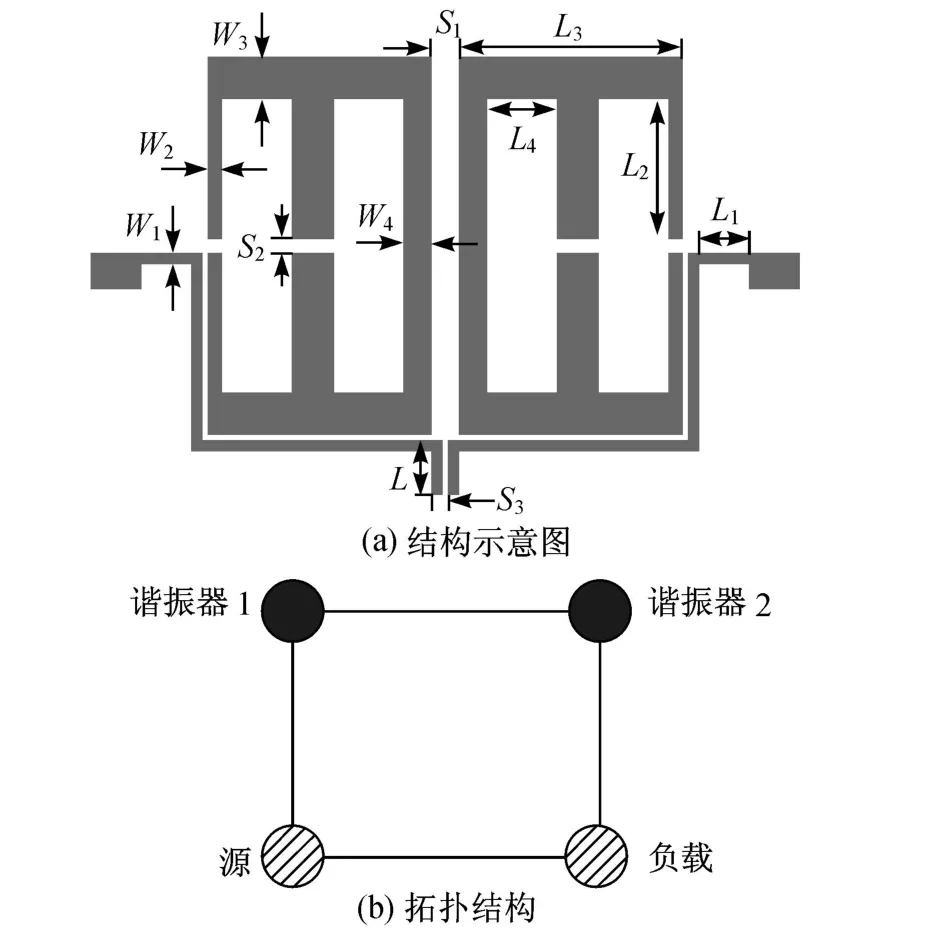
圖 1 濾波器結構Fig.1 Geom etry of the f ilter

1.1 “N+2”耦合矩陣

根據文獻[5]中的推導方法,首先綜合得出基于廣義切比雪夫函數的“N+2”耦合矩陣.由于耦合結構呈現出對稱性,耦合矩陣中的對稱元素源與諧振器 1之間的耦合MS1等于負載與諧振器 2之間的耦合M2L.直接的源與負載之間的耦合 MSL具有容性耦合特性,因此,MSL＜0.根據實際應用中對濾波器性能的要求,設置帶內回波損耗為 -25 dB,2個對稱傳輸零點分別位于歸一化頻率 ±j10處.綜合得到的耦合矩陣

相應的歸一化頻率響應如圖 2所示.有限位置傳輸零點的個數直接依賴于耦合網絡的拓撲結構,它們的具體位置由不同耦合系數的符號和幅值決定[11].

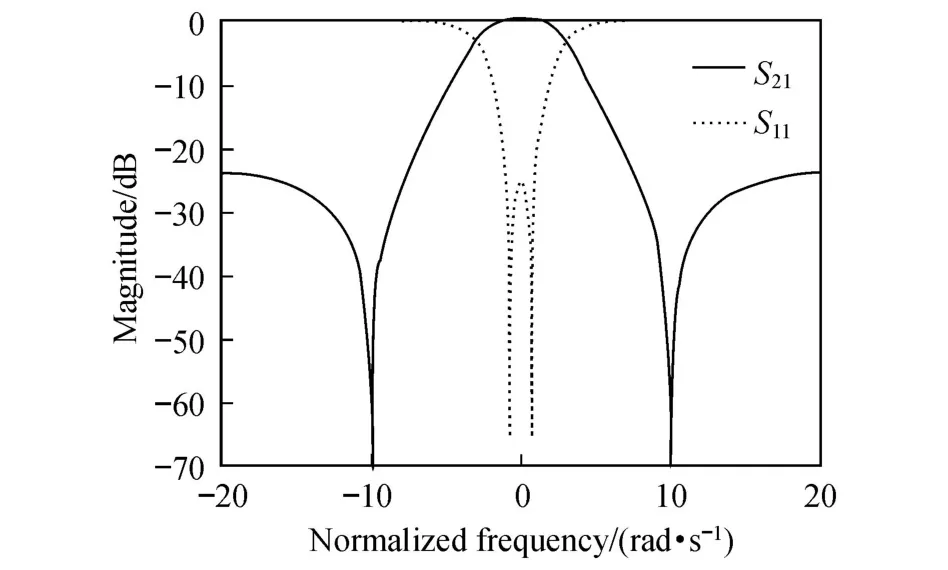
圖 2 歸一化頻率響應Fig.2 Normalized frequency respon se

1.2 新型慢波諧振器

圖 3(a)所示為本工作所提出的新型慢波諧振器的結構,2個相對的開路枝節加載于慢波諧振器的內部,得到更加緊湊的結構.該慢波諧振器在開路端電場占優,閉合端磁場占優.與圖 3(b)所示的傳統的慢波諧振器相比,新型慢波諧振器的開路端寬度尺寸較小,因此,其電場較強,與饋線之間的耦合較強,配合相應的饋線結構能夠實現較小的外部品質系數.

根據文獻[12]中的分析,耦合系數 Kij和外部品質系數Qe可以由以下 2個公式確定:

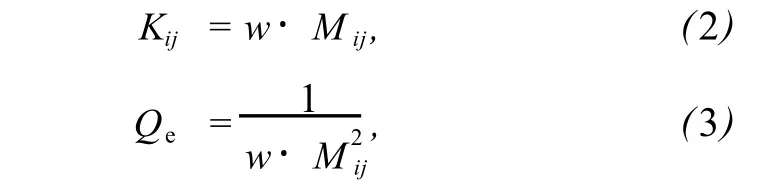
式中,w為帶通濾波器的分數帶寬.圖 4所示為 2個諧振器之間的耦合系數 K12隨耦合距離 S1的變化情況.圖 5為外部品質系數Qe隨耦合長度 L的變化情況.根據圖 4和圖 5,可以方便地得出符合耦合矩陣元素大小的相應濾波器尺寸.本工作所用的仿真工具為基于矩量法的 Sonnet電磁仿真軟件.

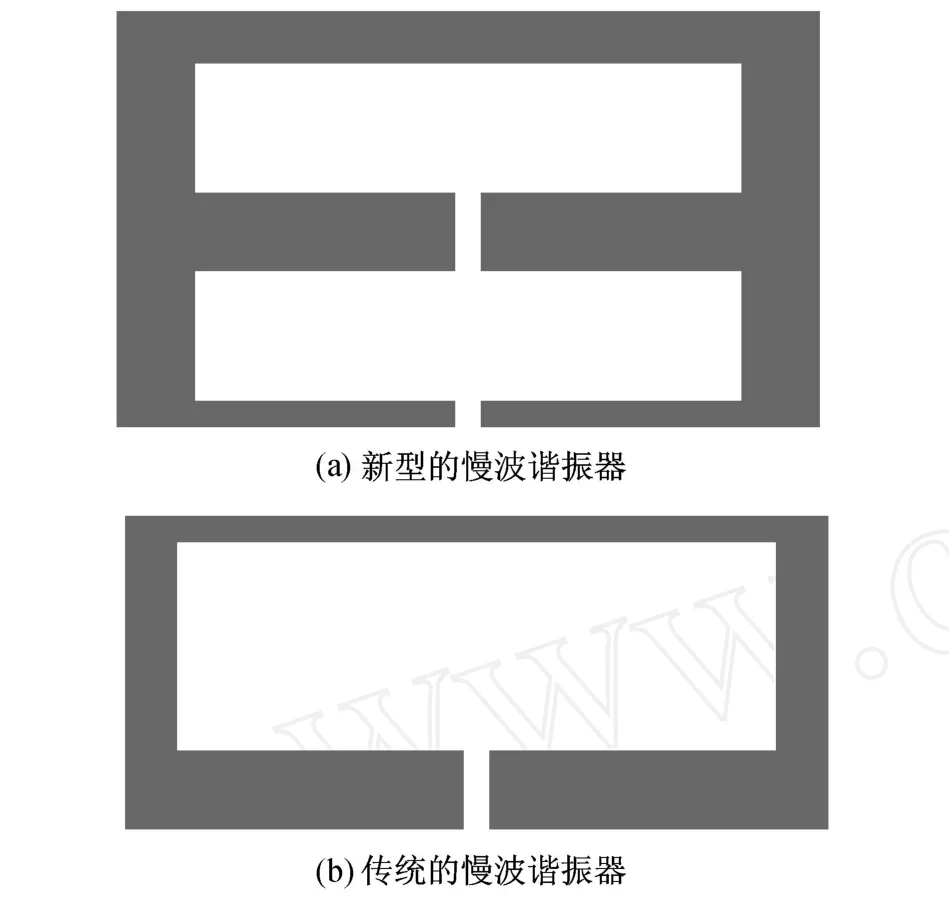
圖 3 慢波諧振器結構Fig.3 Geometry slow-wave resonator

圖 4 耦合系數 K12隨耦合距離 S1的變化曲線Fig.4 Coupling coeff icient K12vs.coupling gap S1

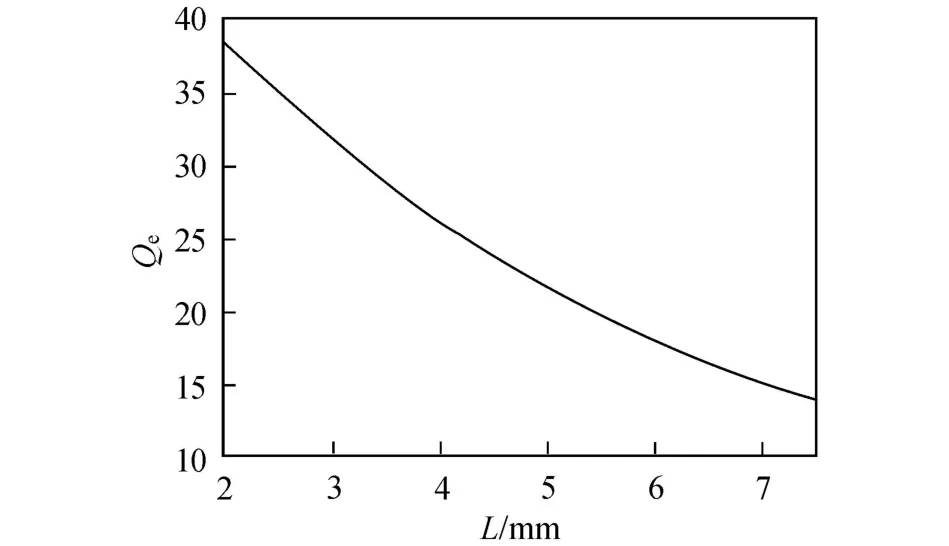
圖 5 外部品質系數 Qe隨耦合長度 L的變化曲線Fig.5 External quality factor Qevs.coupling length L

2 仿真與測試結果

濾波器的中心頻率由諧振器的大小和開路枝節的位置決定.按照無線局域網中 IEEE 802.11a/b的標準,本研究將濾波器的中心頻率設定在 2.4 GHz.根據上述“N+2”耦合矩陣理論,引入源與負載之間的容性耦合.在不同的耦合長度 L下,濾波器的頻率響應發生了較為明顯的變化,如圖 6所示.當 L從0 mm增大到 1.2 mm時,通帶內的回波損耗逐漸減小,阻帶的傳輸零點逐漸靠近通帶,從而兩邊的過渡帶獲得了尖銳的頻率選擇性.同樣,仿真得到的響應特性也可以通過改變公式 (1)中MSL的大小進行理論驗證.

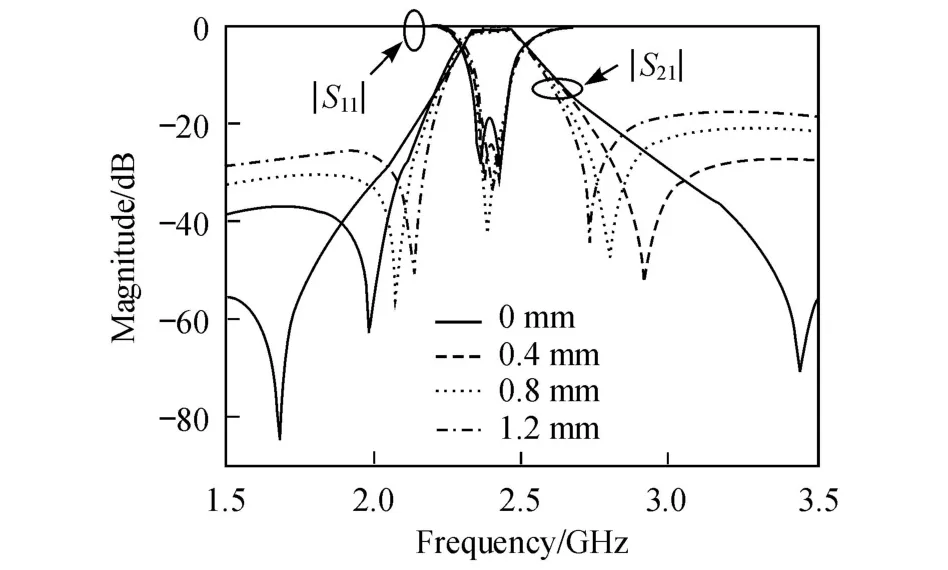
圖 6 不同耦合長度L下頻率響應的變化曲線Fig.6 Frequency responses for var ious coupling length L

濾波器實物如圖 7所示.使用 Agilent 8722ES型矢量網絡分析儀測量該濾波器的 S參數,測量結果和仿真結果如圖 8所示.測量結果表明,該濾波器具有帶內 -24 dB的回波損耗,最小為 1.66 dB的插入損耗,3.3%的分數帶寬,達到了 7.0 GHz優于-20 dB的帶外抑制水平.從圖 8中可以清楚地看到,2個傳輸零點分別位于 2.01和 2.88 GHz頻率處,相應的抑制水平分別為 -56和 -41 dB,這使得過渡帶具有較高的頻率選擇性.插入損耗主要來自于 SMA(small a type)接頭、傳導和介質損耗.

圖 7 濾波器實物圖Fig.7 Photograph of the fabr icated f ilter

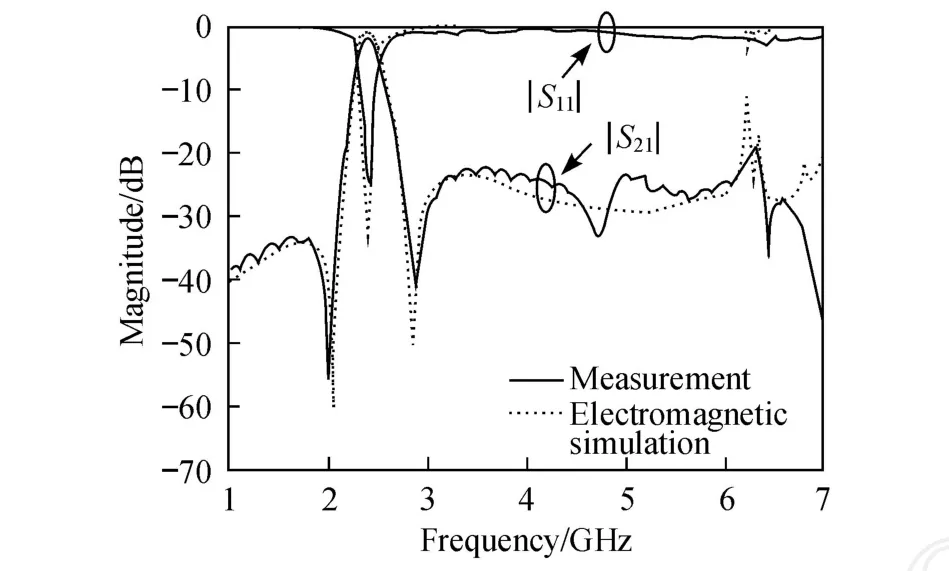
圖 8 實測和仿真頻率響應Fig.8 M easured and sim ulated frequency respon ses

3 結 束 語

本工作采用新型的慢波諧振器結構,設計了一種工作于 2.4 GHz的微帶帶通濾波器.由于利用“N+2”耦合矩陣分析方法,這種濾波器易于設計和優化.測試結果表明,該濾波器具有良好的響應特性,包括通帶內較低的插入損耗、良好的頻率選擇性以及較寬的上阻帶帶寬.實測結果和仿真結果具有良好的一致性,從而驗證了設計的可靠性.因此,該濾波器及其設計方法非常適用于無線局域網系統.

[1] AHN C S,LEE J,KIM Y S.Design flexibility of an open-loop resonator filter using similarity transformation of coup ling matrix[J].IEEEM icrowave and Wireless Components Letters,2005,15(4):262-264.

[2] CHEN YM,CHANG SF,CHANG CC,et al.Design of stepped-impedance combline bandpass filters with symmetric insertion-loss response and wide stopband range[J].IEEE Transactionson M icrowave Theory and Techniques,2007,55(10):2191-2199.

[3] ZHANG X C,YU Z Y,XU J.Design of microstrip dualmode filters based on source-load coupling[J]. IEEE M icrowave and Wireless Components Letters,2008,18(10):677-679.

[4] WANG Y X,WANG B Z,WANG J P.The design of coupled resonator bandpass filter with wide stop-band[J].M icrowave and Wireless Components Letters,2008,18(4):251-253.

[5] CAMERON R J.Advanced coup ling matrix synthesis techniques for microwave filters[J].IEEE Transactions on M icrowave Theory and Techniques,2003,51(1):1-10.

[6] ROSENBERG U,AMARI S.Novel coupling schemes for microwave resonator filters[J]. IEEE Transactions on M icrowave Theory and Techniques,2002,50(12):2896-2902.

[7] TANG C W,CHEN M C.Wide stopband parallelcoup led stacked SIRs bandpass filters with open-stub lines[J].M icrowave and Wireless Components Letters,2006,16(12):666-668.

[8] CHANG Y C,KAO C H,WENG M H.Design of the compact wideband bandpass filter with low loss,high selectivity and w ide stopband [J].M icrowave and Wireless Components Letters,2008,18(12):770-772.

[9] HONG J S,LANCASTER M J.M icrostrip filters for RF/microwave application[M].New York:John Wiley&Sons Inc,2001:392-404.

[10] HUANG X D,CHENG C H.A novel microstrip dualmode bandpass filter with harmonic suppression[J].M icrowave and Wireless Components Letters,2006,16(7):404-406.

[11] AMARI S,ROSENBERG U,BORNEMANN J.Adap tive synthesis and design of resonator filterswith source/loadmultiresonator coupling [J]. IEEE Transactions on M icrowave Theory and Techniques,2002,50(8):1969-1978.

[12] CAMERON R J,KUDSIA C M,MANSOUR R R.M icrowave filters for communication systems:fundamentals,design,and applications[M]. New York:John Wiley&Sons Inc,2007:516-518.

A Novel Bandpass Filter Based on Coupling M atr ix

GAO Shan, XIAO Zhong-yin, CHEN Wen-feng
(School of Communication and Information Engineering,ShanghaiUniversity,Shanghai200072,China)

A novel microstrip bandpass filter(BPF)with two transmission zeros ispresented.This filter has awide upper stopband by using two novel slow-wave resonators.With an“N+2”coupling matrix method,the filter is easy to design and has high frequency selectivity.Measured results show that the filter has good response performances including low insertion loss of 1.66 dB at the center frequency 2.4 GHz,and upper stopband frequency up to 7.0 GHz.These are in good agreementwith simulation.

bandpass filter(BPF);slow-wave resonator;couplingmatrix;transmission zero

TN 713

A

1007-2861(2011)02-0143-04

10.3969/j.issn.1007-2861.2011.02.007

2009-11-03

上海市重點學科建設資助項目 (S30108);上海市科委重點實驗室資助項目(08DZ2231100)

肖中銀 (1964～),男,副教授,博士,研究方向為微波電路.E-mail:zhyxiao@staff.shu.edu.cn

(編輯:趙 宇 )

隨著通信技術的快速發展,具有小型化、寬阻帶、高頻率選擇性等特點的高性能微波濾波器受到了廣泛的關注.改變濾波器的拓撲結構和諧振器結構,是常用的 2種提高濾波器性能的方法.在拓撲結構方面,關于濾波器傳輸零點的研究十分重要.對于N階濾波器,人們普遍研究的是源與負載分別耦合到單個諧振器的濾波器[1-2],這種情況最多只能產生N-2個有限傳輸零點.而文獻[3-4]的研究表明,引入源與負載之間的耦合后,N個諧振器最多能產生N個有限傳輸零點.另外,Cameron[5]和 Rosenberg等[6]提出并改善了基于廣義切比雪夫函數的規范“N+2”耦合矩陣綜合方法,為更多拓撲結構的研究提供了理論依據.

在諧振器結構方面,為了改善濾波器的帶外抑制特性,常用的方法是利用階躍阻抗諧振器或者慢波諧振器結構來實現寬阻帶[7-9].此外,文獻 [10]中還提出用L形饋線結構來實現諧波抑制.盡管傳統的慢波諧振器具有小型化和寬阻帶的優點,但這些濾波器的饋線和諧振器之間的耦合較弱,導致外部品質系數較高,設計的靈活性較差.此外,在這些改進技術中沒有具體的理論公式來確定傳輸零點的位置,增加了調試的難度.