自適應兩階段設計的性質及樣本容量的再估計

言方榮

（中國藥科大學 數學系，南京 210009）

自適應兩階段設計的性質及樣本容量的再估計

言方榮

（中國藥科大學 數學系，南京 210009）

臨床試驗的主要目的是在給定的一些可能有效的治療中找到一個最佳治療，并證明所找到的最佳治療相對于試驗控制組的優效性。文章探討了自適應兩階段試驗設計及其在臨床Ⅱ/Ⅲ期中的應用，并證明了一些性質。通過計算機模擬給出了有效性檢驗的臨界值與樣本容量的關系，指出自適應兩階段試驗所需的樣本容量比傳統的試驗設計方法更少，有較高的倫理學價值和經濟學價值。

臨床Ⅱ/Ⅲ；自適應兩階段試驗設計；優效性檢驗

0 引言

臨床試驗的主要目的是在給定的一些可能有效的治療中找到一個最佳治療，并證明所找到的最佳治療相對于試驗控制組的優效性。傳統的臨床試驗是在臨床Ⅱ期確定一個最佳治療，在臨床Ⅲ期證明治療的優效性，將臨床Ⅱ/Ⅲ期看成兩個獨立的過程。這一方法在實際應用中較為簡單，但確存在較大的風險。一旦在第一階段（臨床Ⅱ期）選擇了一個錯誤的最佳治療，將影響整個試驗過程，甚至導致試驗的失敗。Bischoh和Miller[1]提出了一個自適應兩階段試驗設計方法，即將臨床Ⅱ/Ⅲ期整合考慮，其基本思想是將第一期試驗數據盡可能用到臨床Ⅲ期的優效性檢驗中去，以期盡可能減少整個試驗中的受試人數，并選擇一個較為可靠的最佳治療。這一方法有較好的倫理學和經濟應用價值。近來相關文獻都進行了研究(Bretz,F.[2])等本文將考慮在一般情形下自適應兩階段的相關性質及樣本容量的再估計問題，并通過模擬證明自適應兩階段試驗優于傳統的試驗設計過程。

1 自適應兩階段試驗設計

假設第i個病人在第k段試驗中接受第j個治療，則

其中，i∈{1，2，…，n}；j∈{0，…，t}；k∈{1，2}；Yijk是第 i個病人在第k段試驗中接受第j個治療觀察值，j=0表示控制組，j∈{1，…，t}表示t個治療組；μj為第j個治療的平均效應。設 θ 表示最佳治療方案，則θ贊=argmaxj=1，…，t{μj}。由自適應兩階段設計方法，在試驗的第一階段（臨床Ⅱ期）觀察Yij1，在試驗的第二階段（臨床Ⅲ期）只觀察 Yij2.（j∈{0，}）。 經典的優效性檢驗可用如下多重假設檢驗表示Bechhofer,R.E.[3]:

而對自適應兩階段設計，利用第一階段中期分析的結果，只需檢驗

設第j個治療組有n1個樣本，則在試驗第一階段

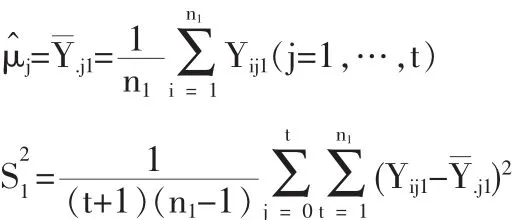
其中v是屬性參數，[·]表示高斯取整函數。由（3）治療組與控制組優效性的檢驗只需比較j=0和j=θ贊。記

下討論基于（4）檢驗統計量的一些性質。

2 基本性質

定理 1 設 n1∈N，n2，min∈N0，V>0，α>0，μj，{j=0，1， …，t}是t+1個處理效應，則檢驗臨界值u是如下方程的解

表1 樣本容量n1與u、v的關系

表2 試驗樣本容量的再估計

3 模擬研究

利用定理1及定理2，通過計算機模擬樣本容量n1與臨界值u與屬性參數v的關系，未知方差σ2與試驗所需總體樣本容量的關系，并與一般的試驗設計相比較。為方面起見，這里僅模擬j=0，1，2情形，即試驗中有一個控制組，兩個對照組。根據FDA相關規定取檢驗的水平α=0.025，檢驗功效1-β=80%，σ2={22，34，61，102，144}，μ1-μ2≥△=4。模擬結果如表 1、表 2。

4 討論

本文討論了臨床Ⅱ/Ⅲ試驗設計的兩階段自適應設計法，將臨床Ⅱ/Ⅲ過程看成是一個整體的過程。充分利用在試驗第一階段所獲得的信息，將它作為第二階段試驗的依據，并用以估計試驗中的未知方差。定理1和定理2分別討論了自適應兩階段設計的一些性質和樣本容量的再估計問題，給出了嚴格的證明。通過模擬，給出了臨床Ⅱ期試驗所需的樣本容量和檢驗臨界值的關系（見表1），并討論了未知方差σ2與試驗所需總體樣本容量N的關系，并與傳統的試驗設計方法作比較（見表2）。結果表明，自適應兩階段設計方法明顯優于傳統的試驗設計方法，大大減少了試驗所需樣本容量。由此可見自適應兩階段設計方法在臨床試驗設計中有明顯的倫理學價值和經濟學價值。當然，本文僅僅討論了平衡設計的問題，即假定每組試驗設計所需的樣本容量是相等的，對于非均衡設計的問題有待進一步的研究。

[1]Bischoff,W.,Miller,F.Adaptive Two-Stage Test Procedures to

Find the Best Treatment in Clinical Trials[J].Biometrika，2005,92.[2]Bretz,F.,Schmidli,Racine,A.,Maurer,W.Confirmatory Seam

less Phase II/III Clinical Trials with Hypotheses Selection at Interim:General Concepts[J].Biometrical J.，2006,48.

[3]Bechhofer,R.E.,Dunnett,C.W.,Sobel,M.A Two-Sample

Multiple Decision Procedure for Ranking Means of Normal Popu

lations with a Common Unknown Variance[J].Biometrika，1954,41.[4]Liu,Q.,Pledger,G.W.Phase II and III Combination Designs to Accelerate Drug Development[J].Amer.Statist.Assoc，2005,100.

[5]Maca,J.,Bhattacharya,S.,Dragalin,V.,Gallo,P.,Krams,M.Adaptive Seamless Phase II/III Designs– Background,Operational Aspects,and Examples[J].Drug Informat，2006,40.

[6]Miller,F.Variance Estimation in Clinical Studies with Interim Sample Size Reestimation[J].Biometrics，2005,61.

[7]Wang,J.An Adaptive Two-Stage Design with TreatmentSelection Using the ConditionalError Function Approach[J].Biometrical，2006,48.

（責任編輯/亦 民）

O212

A

1002-6487（2011）03-0021-02

言方榮（1978-），男，江蘇常州人，研究方向：生物統計。