結合實際談數學教學中如何培養學生的觀察能力

遼寧 李海波

結合實際談數學教學中如何培養學生的觀察能力

遼寧 李海波

數學觀察能力是指在學習、生活中積極主動地獲取數學信息,聯系數學知識,構造數學模型,進而認識數學問題并解決數學問題的重要能力。本文從激活學生的觀察興趣，培養學生的觀察能力；增強觀察的目的性，提高學生的觀察能力；邊觀察邊思考，提高解決實際問題的能力幾個方面對培養學生的觀察能力進行了闡述。

數學；觀察；興趣；觀察能力

教育的目的在于知識的傳授和能力的培養。其中能力的培養對提高教學質量，提高受教育者的素質是非常重要的。對教師而言，他的工作不只是簡單地傳授知識，而應該是教會學生獲取知識的同時，獲得比知識更重要的觀察、分析、概括、解決問題的實際能力。

數學教學，實質上是思維活動的教學，其教學過程是在教師的主導作用之下，使學生通過認識——實踐——再認識——再實踐這個過程掌握知識，獲得分析問題、解決問題的能力。在這個過程中作為學習主體的學生，它不是知識的消極接受者，教師也不可能機械地把知識灌輸到學生頭腦中去，要想把人類積累的認識成果轉變為學生的知識財富，進而轉化為學生的智力才能，必須通過學生自己的積極思考和參與，充分調動學生學習的主動性，才能取得較好的教學效果。針對學生在學習中不善于觀察、分析、概括的情況，教學中我著重在以下幾個方面進行了嘗試，并取得了較好的效果。

一、激活學生的觀察興趣，培養學生的觀察能力

心理學認為：觀察是一種有目的、有計劃、主動并有思維參與的知覺過程；它是一種比隨意注意更為自覺的積極的感知過程。數學觀察能力是指人們有目的、有計劃、有選擇的、較持久的數學感知能力,是人們在學習生活中積極主動地獲取數學信息,聯系數學知識,構造數學模型,進而認識數學問題并解決數學問題的重要能力。培養觀察能力是全面提高學生素質的重要環節。

培養學生的觀察能力，首先要使學生對所觀察的對象產生興趣，激發他們“求知”的欲望。例如講等比數列前n項和公式時，我先給學生出示了一個國際象棋的棋盤，然后講了一個國王賞麥的故事：相傳古印度宰相達依爾發明了國際象棋。當時的國王大為贊賞，就問他想要什么。達依爾說：“請在棋盤的64個方格上，第一格放1顆麥粒，第二格放2顆麥粒，第三格放4顆麥粒，依次類推，每一格放的麥粒數都是前一格的兩倍，直到第64格，請您給我足夠的麥粒以實現上述要求。”國王覺得這并不是很難辦到的,就欣然同意了他的要求。這時，我啟發學生想：“國王要給達依爾多少麥粒？”結果學生通過觀察很快就找出答案。各個格子里的麥粒數依次是：1，2，22，23，…，263，于是發明者要求的麥粒總數就是1+2+22+23+…+263，接著引導學生把上面的問題看成是等比數列 1，2，22，23，…，263的前64項的和，同時，請學生大膽預測麥粒的重量將是多少？產生懸念,然后一步步引導學生推導出等比數列的前n項的和公式。在公式推導后讓學生運用公式算出發明者要求的麥粒總數是：18446744073709551615（粒），重約 7000億噸。這樣，首尾呼應，既培養了學生的觀察能力，又激活了學生學習數學的興趣，同時也讓學生明白數學和生活息息相關，把學以致用的思想滲透到課堂中。

二、增強觀察的目的性，提高學生的觀察能力

觀察是思維的觸角，是思維的前提，不懂得觀察就不懂得思維，要培養學生嚴密的邏輯思維能力，就必須教給學生觀察的方法。數學中有許多概念是由生產生活中的實際模型抽象出來的，因此這一類的概念教學中，教師要通過演示，展示生產生活中的實際模型，盡可能地讓學生通過觀察概括出其本質屬性。

例如：在數列極限概念的教學中，我采取的做法是：首先引導學生觀察電腦動態演示做圓的內接正三邊形、圓的內接正六邊形、圓的內接正十二邊形、圓的內接正二十四邊形、圓的內接正四十八邊形…，（重復三次），然后提出問題：隨著圓內接多邊形邊數的增加，圓內接多邊形與圓之間,圓內接多邊形的周長與圓的周長之間存在什么樣的關系。這時學生會在觀察的基礎上回答出：隨著圓內接多邊形邊數無限增加，圓內接多邊形越來越貼近圓，圓內接多邊形的周長越來越接近圓的周長。這時，我再總結以下的結論：設圓的半徑為R，圓內接正三角形，正四邊形，正五邊形…，正n邊形的周長所組成的數列 P3，P4，P5，…，Pn，…，則隨著圓內接多邊形邊數n無限增大，圓內接多邊形的周長Pn無限地趨向于圓的周長2πR。同時告訴學生：“割之彌細，所失彌少，割之又割，以至于不可割，則與圓合體而無所失矣。”這種方法就是三國時的數學家劉徽提出的“割圓求周”的方法。從而激發學生的民族自尊心和愛國主義思想情感。接著引導學生把上面的問題看成是無窮數列的項數n無限增大時,數列是否無限地趨近一個常數C的問題。從而引出數列極限的定義。這樣進行概念教學，將使學生從認識上初步完成實驗——觀察——感性——理性的認識過程，從而調動學生學習的積極性，讓學生的感知活動按預定的方向和目標進行，使他們從被動地接受任務進行觀察轉變為主動地、有意識地觀察，增強了觀察的目的性，也提高了學生的觀察能力。

三、邊觀察邊思考，提高學生解決實際問題的能力

思維源于觀察，觀察是進行思維的基礎。只有在觀察中思考，在思考中觀察，才能喚起聯想，進行分析、綜合、比較、抽象、概括等思維活動，才能真正理解教學內容，掌握知識，提高解決實際問題的能力。

例如：在二項式定理教學中，二項式定理展開式中各項的系數很難掌握，教學中，我首先提出問題:今天是星期二,再過7天,還是星期二;再過 15天呢?再過 8100天呢?（注:8100=（7+1）100），8100=（7+1）100的展開式是什么呢?聯系實際,引發學生了解（a+b）n=?的興趣。其次，列出學生已掌握的（a+b）0，（a+b）1，（a+b）2，（a+b）3的展開式

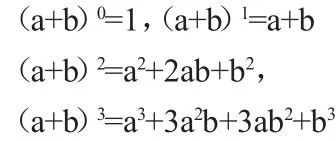
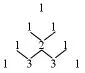
將上述展開式的系數排成三角形如圖：

這時讓學生觀察總結展開式的系數規律，即右圖三角形中每行數的規律。學生很快就能總結出：“表中數據除1以外的每個數等于它左右肩上兩個數的和”接下來請同學們按此規律排出以下的行為：

右面這個表稱楊輝三角，它是宋朝數學家楊輝的杰作，楊輝三角是我國數學發展史上的一個成就。它比歐洲人的帕斯卡三角要早四百多年。

猜想：（a+b）4=?，（a+b）5=?

按照表中數據的規律，不必用多項式乘法，學生就能很快地寫出：

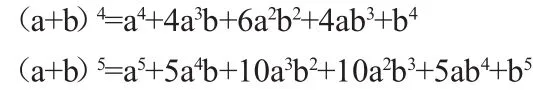
并可根據數學規納法的知識自己推出一般的（a+b）n展開式的系數規律。

總之，現代數學離不開觀察，觀察可以使我們獲得豐富的感性材料，從而為進一步思維、揭示事物的本質規律奠定基礎。在數學教學中，只有注重培養學生的數學觀察能力，不斷教會學生會觀察、善于觀察，才能不斷發展學生的數學思維能力，培養學生良好的思維品質，從而提高學生分析問題、解決問題的能力。

【1】張成恩.數學教學對學生觀察能力的培養.中國科技信息，2005年12期.

（作者單位：遼寧城市建設職業技術學院）

（編輯 劉麗娜）