用算子刻畫的兩類n次對稱p葉解析函數
李書海,趙翠新
(赤峰學院 數學學院,內蒙古 赤峰 024000)
用算子刻畫的兩類n次對稱p葉解析函數
李書海,趙翠新
(赤峰學院 數學學院,內蒙古 赤峰 024000)
本文引進并研究用算子刻畫的的 p 葉對稱解析函數子類 Sn,m,j(λ,β,p)和 ?n,m,j(λ,β,p).討論兩類函數上的積分算子凸性問題,并推廣相關結果.
解析;算子
1 引言
Sn(j,p)(j,n,p∈N)表示在單位圓盤 U={z:|z|<1}內對稱解析函數的全體所成的類.用 Pn,j(β)(0≤β<1)表示U內β級正實部函數類:
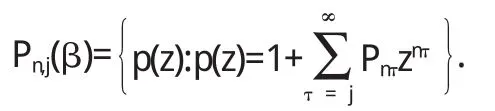
用 S*n,j(p,β)和 Kn,j(p,β)分別表示 Sn(j,p)中的 p葉 β 級星象函數類和p葉β級凸象函數類.
令
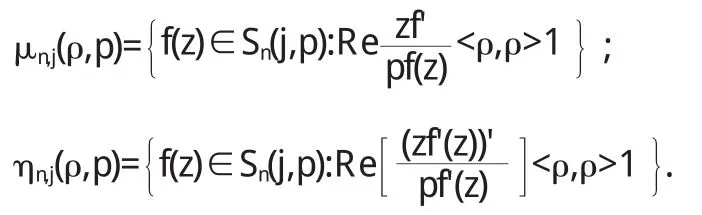
文[1]-[3]中討論了函數類 μ1.1(ρ,1)和 η1,1(ρ,1)的性質.
我 們 在 函 數 類 Sn(j,p)上 引 進 S a l a g e a n算 子:設 f(z)∈Sn(j,p)則
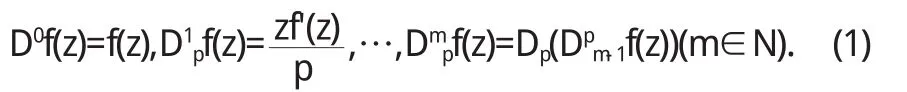
其中
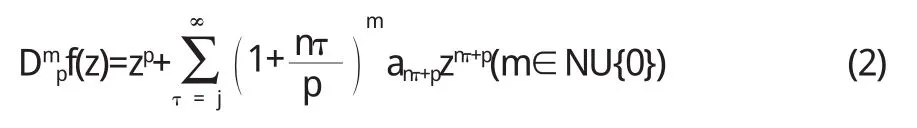
顯然 Dm1f(z)為[4]中定義的 S a l a g e a n算子.
本文引進兩類對稱解析函數:
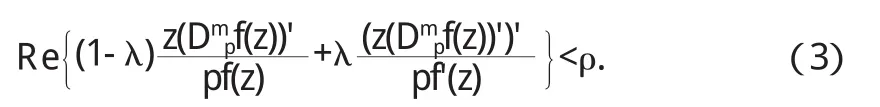
稱 f(z)屬于函數類 ?n,m,j(λ,ρ,p).顯然
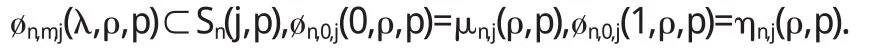
定 義 2 設 λ≥0,-1≤β<1,若函數 f(z)∈S n(j,p),滿足條件:
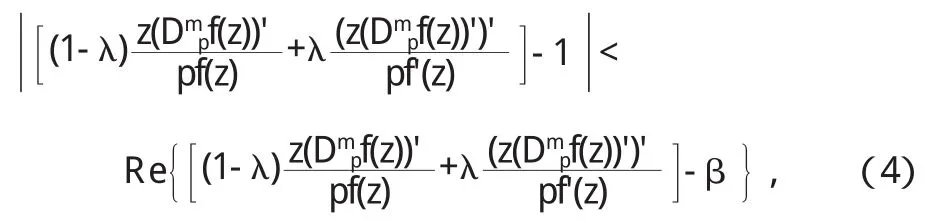
稱 f(z)屬于函數類 Sn,m,j(λ,β,p).在文[5][6]中研究了函數類S1,0,1(0,β,1).
在S上引進一類新的積分算子:

從
(5)式還得到

當 p=1時,(6)(7)式為文[5][6]中引進并研究的積分算子.
本 文 中 我 們 討 論 Sn,m,j(λ,β,p)和 ?n,m,j(λ,β,p)上 的 積 分 算 子Fn,α1,L,αk(m,λ;z)的性質,推廣相關結論并得到有趣的結果.
2 主要結果及其證明
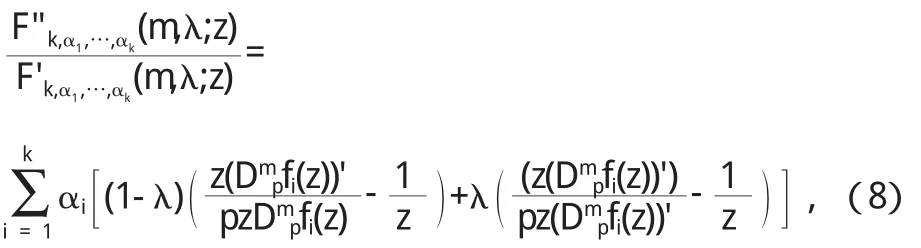
即
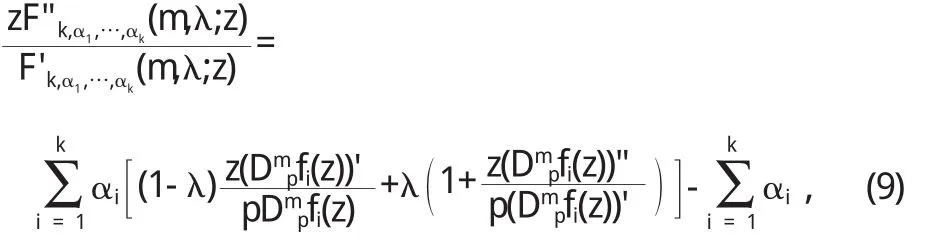
從(9)式推出
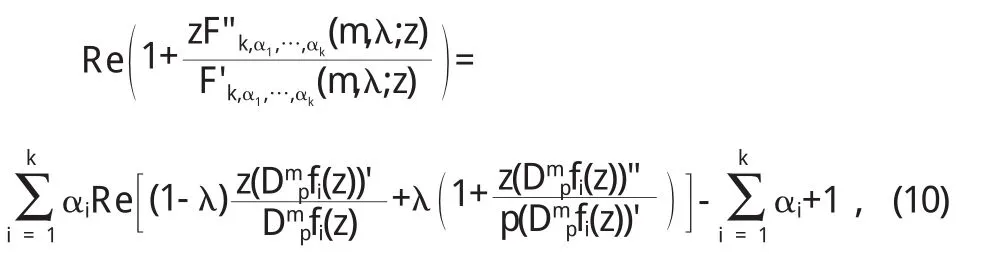

定 理 2 設
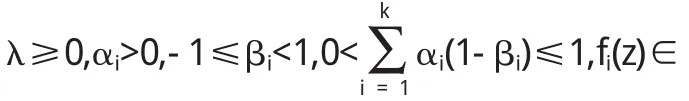
Sn,m,j(λ,βi,p),i=1,2,…,k,則積分算子 Fk,α1,…,αk(m,λ;z)∈Kn,j(γ,p),其
證明 對(5)式兩端,用定理 1相同的方法得到
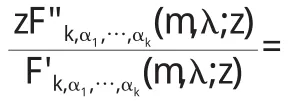
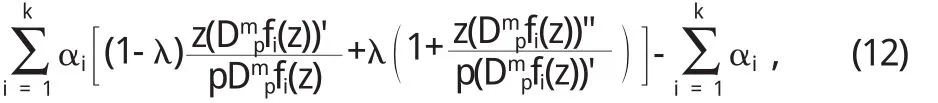
從(1 2)式推出
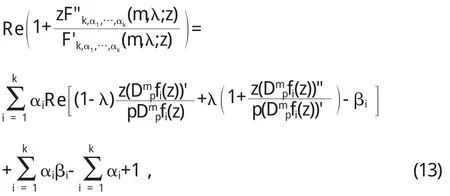
因為 fi(z)∈Sn,j(λ,βi),i=1,2,…,k,因此從上式得到
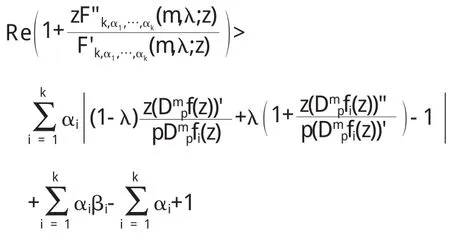
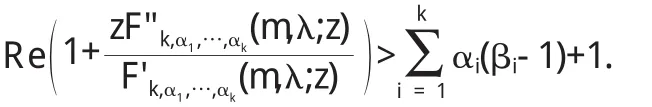
注:由定理 1和定理 2容易得到文[3]-[5][6]中的主要結果.
〔1〕B.A.Uralegaddi,M.D.Ganigi,and S.M.Sarangi,U-nivalent functions with positive coefficients[J].Tamkang Journal of Mathematics,1994,25(3),225–230.
〔2〕S.Owa and H.M.Srivastava, Some generalized convolution properties associated with certain subclasses of analytic functions[J].Journal of Inequalities in Pure and Applied Mathematics,2002,3 (3),Article ID 42,13 pages.
〔3〕Daniel Breaz,A Convexity Property for an Integral Operator on the Class [J].Journal of Inequalities and Applications Volume 2008,Article ID 143869,4 pagesdoi: 10.1155/2008/143869.
〔4〕G.S.Salagean,Subclass of univalent functions[J].Lecture Notes in Math.,Springer,Berlin,1983,1013,362-372.
〔5〕D.Breaz and N.Breaz,Two integral operators[J].Studia Universitatis Babes?-Bolyai,Mathematica,2002,47 (3),13–19.
〔6〕Daniel Breaz,A Convexity Property for an Integral Operator on the Class [J].Journal of Inequalities and Applications, 2008,Article ID 143869,4 pages.
O 1 7 4.5 1
A
1673-260X(2011)04-0003-02
內蒙古自然科學基金資助項目(No.2009MS0113)

