接地導體薄圓筒與不共軸平行導體圓筒的電勢和電場
范夢慧
(貴州民族學院 理學院,貴州 貴陽 550025)
接地導體薄圓筒與不共軸平行導體圓筒的電勢和電場
范夢慧
(貴州民族學院 理學院,貴州 貴陽 550025)
利用復數坐標系上的保角變換,分兩種情況討論接地導體薄圓筒與不共軸平行導體圓筒之間的電勢和電場的分布函數,所得兩種函數表達形式相似.
保角變換;接地導體薄圓筒;平行導體圓筒;電勢分布;電場分布
在 教 材 中[1,2,3],通 常 以 兩 無 限 長 共 軸 圓 筒 為 例 利 用 高 斯定理和電勢定義式計算其電場和電勢的分布,然而對于兩不共軸無限長圓筒直接用教材中的方法很難得到其電場分布.本文分接地無限長導體薄圓筒與筒外無限長平行導體圓筒及接地無限長導體薄圓筒與筒內不共軸的無限長平行導體圓筒兩種情況,運用保角變換法[4]把不共軸的兩圓筒變換為共軸兩圓筒直接由無限長圓筒外的電勢直接算出其電勢和電場分布函數.
1 接地導體薄圓筒與筒外平行導體圓筒的電勢與電場分布
半徑為 a,單位長度上電荷為 q的無限長圓筒 C 1與筒外半徑為 b接地無限長導體薄圓筒 C 2平行,兩軸相距為 d(d>a+b).因在垂直于兩圓筒軸線的所有平面上電場的分布均相同,所求的電場為平行平面場,可取任一截面為復平面z,以導體薄圓筒 C 1的圓心為原點,以兩軸的連線為 y軸建立坐標系如圖1所示,討論其電勢和電場在該復平面上的分布.為了簡便地求出電勢的分布,利用保角變換可將 C 1和 C 2變 為 同 心 圓 ,在 z平 面 上 選 點 A(0,i y1)和 點 B(0,i y2),兩點關于圓 C 1和圓 C 2均對稱,y1和 y2所要滿足的方程組如下

解方程組(1)得
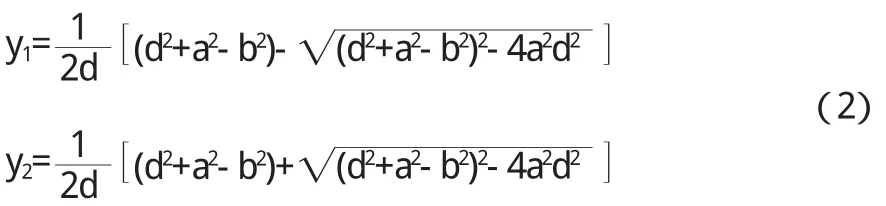
設所求的變換為分式線性變換
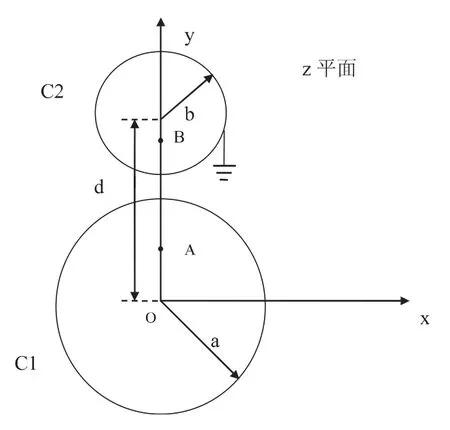
圖 1 z平面上兩圓筒的截面(d>a+b)

通過變換把 z平面的 A點變為 ζ平面的原點 ζ=0,把點B變為 ζ平面的無限遠點 ζ=∞.圓 C1變為 ζ平面上以原點ζ=0為圓心的圓 C1,圓 C2變為 ζ平面上也是以原點 ζ=為圓心的圓 C2(如圖 2所示),這樣圓 C1和 C2是同心圓.
為了計算同心圓 C1和 C2的半徑 a和 b.在 z平面上的圓 C 1上取一點 z1=-a i,在圓 C 2上取一點 z2=(d+b)i,代入式(3)得
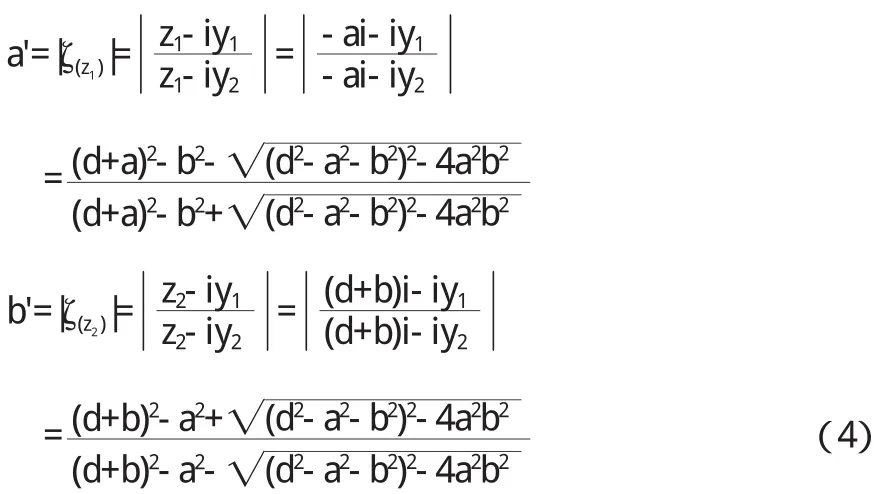
由于在保角變換后相應區域的總電荷量保持不變,則在ζ平面上,單位長度電荷為q的無限長圓筒外的電勢直

圖 2 ζ平面上的兩圓筒的位置(d>a+b)
接寫為

其中 k為實常數,其值可由圓 C2'為零點電勢確定
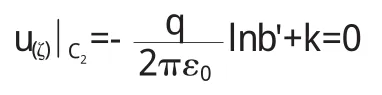
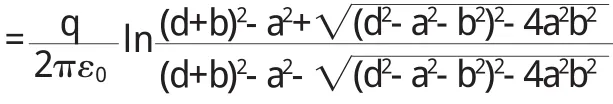
把 k值代入式(5)得
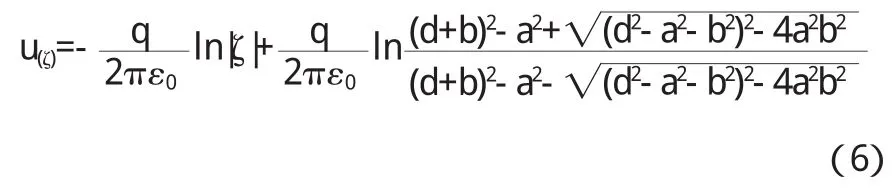
將 u(ζ)變回到 z平面 ,可得接 地無限長導 體薄圓筒與筒外無限長平行導體圓筒之間的電勢分布函數為
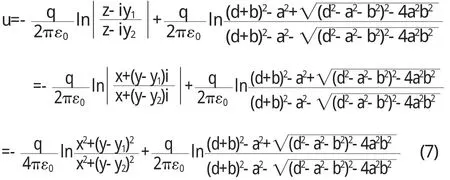
z平面上接地無限長導體薄圓筒與筒外無限長平行導體圓筒之間各點的電場由E→=-▽u得:
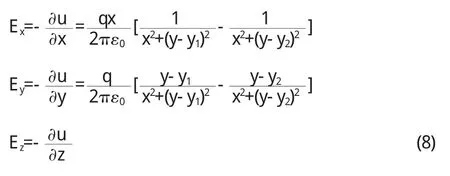
再將(2)式中 y1,y2值代入上式即可.
導體圓筒 C 1和 C 2內各點的電場由導體靜電平衡條件得
圓筒 C 1是一等勢體,其電勢由式(4)和式(5)算出
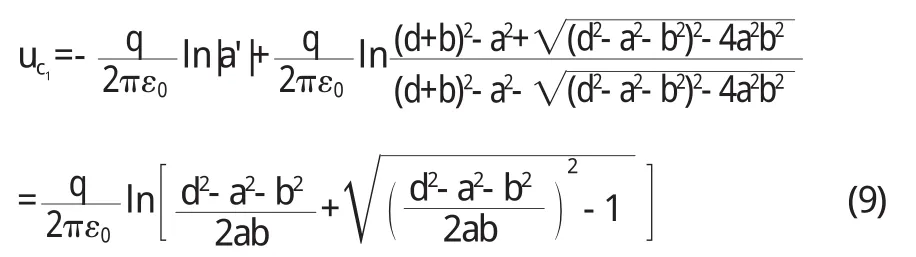
2 接地導體薄圓筒與筒內不共軸的平行導體圓筒的電勢與電場分布
半徑為 R1的接地無限長導體薄圓筒 G 1與筒內半徑為R2單位長度上的電荷為 q的無限長導體圓筒 G 2,兩軸平行,相 距為 D(D 圖 3 z'平面上兩圓筒的截面(D 為把 G 1和 G 2變為同心圓,在 z'平面上取與圓 G 1和圓G 2均對稱的兩點(0,i y1)和(0,i y2),則有方程組 解方程組(1 0) 同理,算出經保角變換后的同心圓 G 1'和 G2'的半徑 R1'和R2'(R1'>R2',圓 G1'接地),圖略. 在經保角變換后的ζ平面上接地兩導體圓筒之間的電勢寫為 其中 k'為實常數,其值可由圓 G1'為零點電勢確定 得 代入(1 3)式 將 u(ζ)變回到 z'平面,可得其電勢分布函數為 z'平面上接地無限長導體薄圓筒與筒內不共軸的無限長平行導體圓筒之間各點的電場由E→=-▽u得: 再將(1 1)式中 y1,y2值代入上式即可. 圓筒 G2是一等勢體,其電勢由式(1 2)和式(1 4)算出 利用保角變換法把不共軸的兩無限長圓筒變為共軸的兩無限長圓筒,從而簡便算出其電場與電勢的分布函數.對于所討論的上述兩種情況,接地導體薄圓筒與不共軸的平行導體圓筒之間的電勢與電場分布函數表達形式相似,只是參數不同.不共軸兩平行導體圓筒之間的電場也可由鏡像法求出,由于篇幅原因,本文不再進行闡述. 〔1〕趙 近 芳.大 學 物 理 學 (下)[M].北 京 :北京 郵 電 大 學 出 版社,2008:45-46. 〔2〕馬文蔚.物理學(中)[M].北京:高等教育出版社,1999:54. 〔3〕張 三 慧.大 學 基 礎 物 理 學 (下 )[M].北 京 :清 華 大 學 出 版社,2003:375. 〔4〕梁昆淼.數學物理方法[M].北京:高等教育出版社,1998:433-434. O 4 4 1.1 A 1673-260X(2011)04-0022-03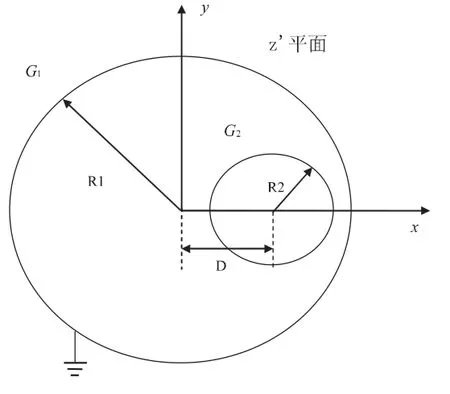


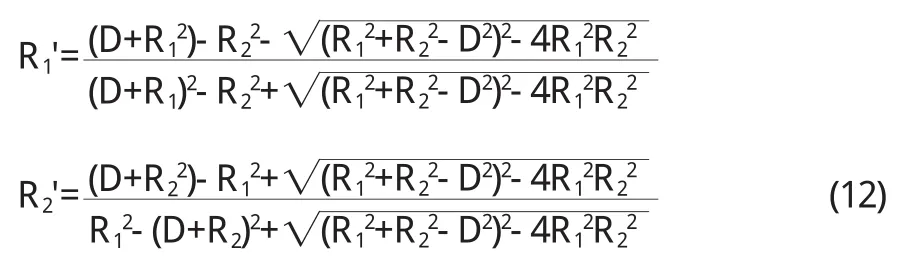

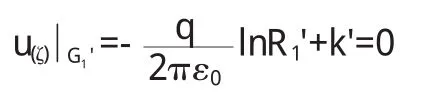
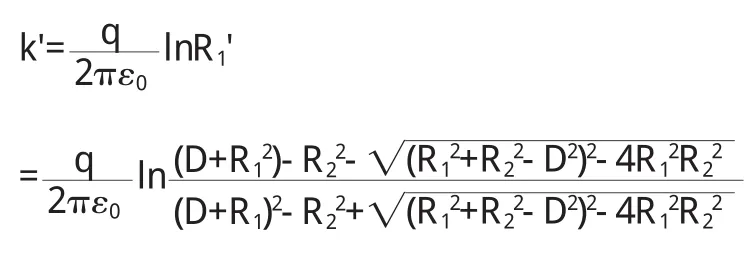
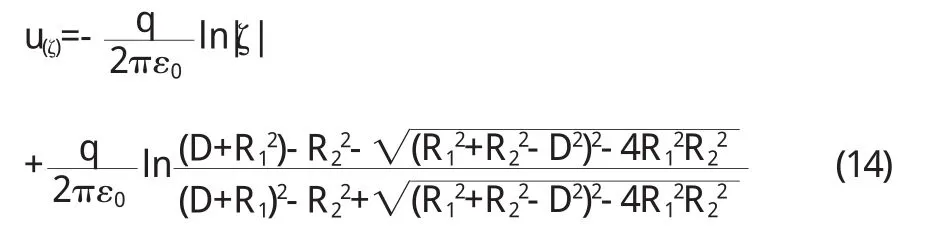
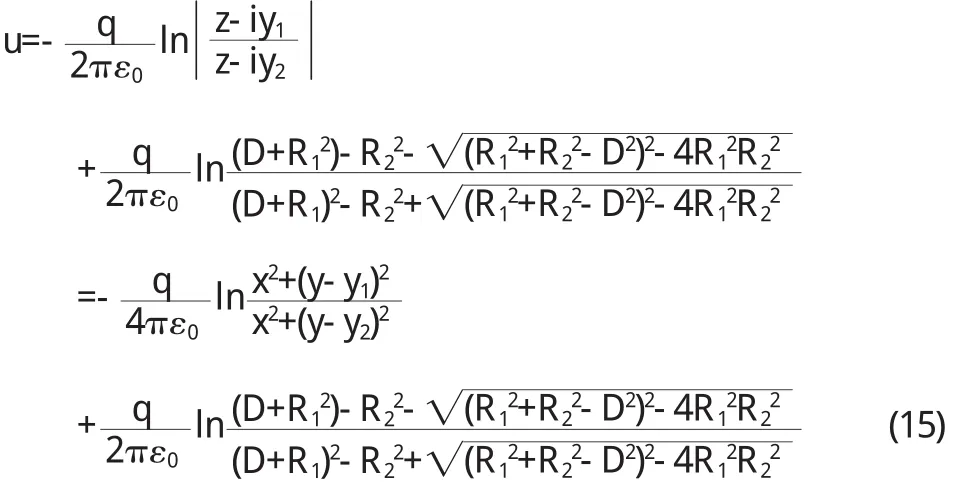
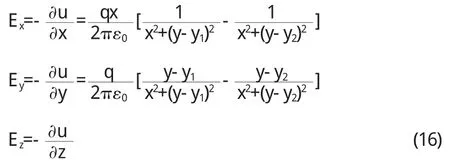
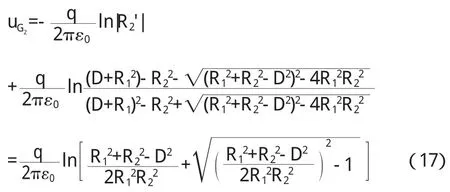
3 結束語

