DEA及其在上市公司融資效率分析中的應用研究
鮑金良 胡偉
DEA及其在上市公司融資效率分析中的應用研究
鮑金良 胡偉
近些年來,數據包絡分析被用來評估很多不同種類實體效益的應用。其中一個非常重要的原因就是,因為經常有很多未知的復雜的因素,使得輸入活動和輸出活動存在很多種聯系。但是數據包絡分析卻不需要考慮這些聯系,因此它為解決這些情況提供了可能。本文簡略介紹了DEA分析方法中的兩個常用模型,并且以創業板在2011年1月份上市的15家公司為例,對其進行了DEA效率分析。
DEA;常用模型;融資效率
一、DEA方法簡介
數據包絡分析(Data Envelopment Analysis,DEA),是一種測度效率的非參數方法。它是基于法雷爾的前沿生產函數思想,能夠評價具有相同類型的投入產出的若干決策單元(DecisionMakingUnits,DMU)的相對效率。由于任何一個生產過程都可以看成是一個生產單元在其可能的范圍內,通過一定生產要素的投入,而得到一定數量的產出的活動。而且活動的目的都是盡可能的以最小的投入,達到最大的產出。由于從生產要素的投入到最后的產出之間,都需要經過一系列決策才能實現。這種需要決策的單元被稱為決策單元(DMU)。同類型的DMU是指具有如下特征的DMU集合:第一,它們具有相同的目標和任務;第二,它們具有相同的外部環境;第三,它們具有相同的輸入、輸出指標,且其值為非負。
假設某DMU在一項經濟活動中的輸入指標為x=(x1,x2,…,xm)τ,輸出指標為y=(y1,y2,…,ym)τ。定義T={(x,y)|輸入指標x能生產輸出指標y}為所有可能的生產活動所構成的所有生產可能集。而由(xj,yj)(j=1,2,…,n)組成的集合T={(x1,y1),(x2,y2),…,(xn,yn)}為參考集。
為了研究方便,我們假設所有生產可能集均滿足下列四條公理:
(1)凸性:對于任意的(x,y)∈T和(x′,y)∈T,μ∈[0,1]則有
μ(x,y)+(1-μ)(x′,y)∈T
即如果用輸入指標x,x′分別和μ,(1-μ)相乘后的和作為新的輸入指標,那么可以得到和原來產出相同倍數的和的新產出。
(2)錐性:若(x,y)∈T及k≥0,則有
K(x,y)=(kx,ky)∈T
即如果用原輸入的k倍作為新的輸入,則能夠得到原產出的k倍。
(3)無效性:設(x,y)∈T,若x′≥x,則(x′,y)∈T;若y′≤y,則(y,y′)∈T。即在原來生產活動的基礎上,增加投入或減少產出是可行的。
(4)最小性:生產可能集T是滿足上述條件的所有集合的交集。
二、DEA方法的常用模型
目前,常用的DEA模型為C2R評價模型和C2GS2評價模型。C2R模型構建過程如下:設有n個決策單元,每個決策單元均有輸入指標xj=(x1,x2,…,xm)τ,輸出指標y=(y1,y2,…,ym)τ。對于任意決策單元DMU基于凸性、錐型、無效性和最小性公理假設,有生產可能集:

可以得到DEA的C2R 模型:
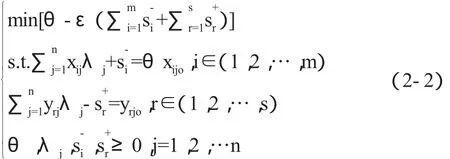
其中,m、s分別表示輸入指標、輸出指標的個數;xijo、yrjo分別表示第jo個DMU的第i項輸入和第r項輸出;s、s表示松弛變量;ε為非阿基米德無窮小量,在計算中為正值的無窮小。
C2GS2模型構建如下對DMU僅基于凸性、錐型和無效性個公理假設,有生產可能集:

可以得到以下模型:

其中各符號意義表示同上。
三、評價模型的經濟解釋
通過上述部分構建的DEA模型,將目標DMU的投入產出指標代入,計算出對應的DMU的融資效率值。
在模型(2-2)中,當最優解為:
(1)θ*=1,s=0,s=0,則稱決策單元j0為DEA有效(C2R),即決策單元j0在原投入X0基礎上能夠得到的產出Y0已經達到最優。其中系數θ可以理解為決策單元DMUj0投入向量的“壓縮系數”,是DEA的相對效率值。
如果θ*=1,s=0,=0,該決策單元同時為規模報酬不變和技術效率最佳。也就是說不僅僅投入不可能等比減少,同時也不存在“過量”投入和“虧量”產出,該決策單元處于有效狀態,即DEA有效(C2R)。
(2)θ*=1,s≠0,或≠0,則稱決策單元j0為DEA弱有效(C2R),即決策單元j0的部分投入Xi0可以減少s-*而保持原產出Y0不變,或者在保持原投入X0不變的情況下,使得部分產出Yj0提高s+*。
如果θ*=1,但是s,s不全為零,則表明非同時規模報酬不變和技術效率最佳。雖然投入已經不用等比減少,但是投入和產出上仍然有不足之處,某些方面仍存在“過量”投入或者“虧量”產出。沒有達到最佳,因此為DEA弱有效(C2R)。
(3)θ*<1,且s≠0,s≠0,則稱決策單元j0為DEA無效(C2R),即決策單元j0的投入不當,可以通過將原投入X0按θ等比例減少,而使原產出Y0保持不變。
如果0<θ*<1,則表明該決策單元的投入不當,可以做全方面的等比減少,也就是說該決策單元非DEA有效(C2R)。
在模型(2-4)中,當最優解為:
(1)θ*=1,0,=0,則稱決策單元j0為DEA有效(C2GS2),即決策單元j0在原投入X0的基礎上,獲得的產出Y0已達最優。即表明該決策單元技術效率最佳。
(2)θ*<1,或s≠0,s≠0,則稱決策單元j0為DEA無效(C2GS2)。若s≠0,表明存在“超量”投入;若s≠0,表明存在“虧量”產出;若0<θ*<1,表明該決策單元投入不當,可以做全面的等比減少,這些均屬于非技術有效。
在現有的DEA模型中,如果僅就有效性而言的話,C2R模型可以用來評價決策單元是否同時為規模有效和技術有效的總體有效,而C2GS2模型僅僅只評價技術效率是否為最佳,把這兩者結合起來,便可以對決策單元規模效率和技術效率做出綜合的評價。
四、DEA方法在上市公司融資效率分析中的應用
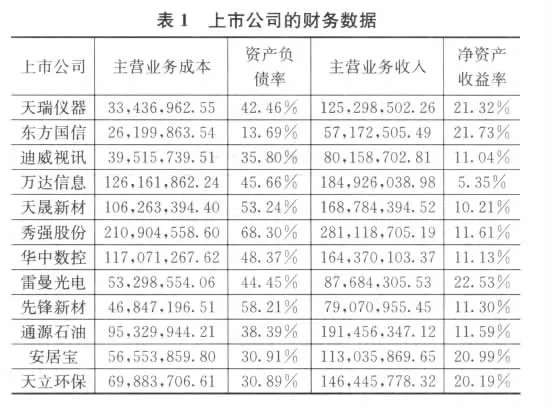
本文以2011年1月份在創業板上市的15家上市公司為樣本,通過DEA方法來測量它們的融資效率。要用DEA方法來測量融資效率的時候,首先需要確定DMU的輸入輸出指標。本文將主營業務成本和資產負債率作為輸入指標,將主營業務收入和凈資產收益率作為輸出指標。指標的數據的均來源于各上市公司經過審計的招股說明書,且均為截止2010年6月30日時的半年財務數據。具體如表1所示。

目前,DEA分析軟件有很多,例如:DEA-SOLVER,DEA-FRONTIER,WINQB等。本文使用DEA分析軟件為DEA-SOLVER_Pro5來進行數據分析處理。在分析指標之前,需要對各指標進行無量綱化。本文使用功效系數法。功效系數法下的無量綱化函數關系如下:
設max1sisn=Zij=aj(aj為第j項指標的最大值),min1sisnZij=bi(bi為第j項指標的最小值),則Zij∈[0.1,1.1]。

處理后的數據如表2所示。
使用DEA-SOLVER_Pro5來處理上表經過無量綱化后的數據,處理后的得到表3。

根據Michael Norman與BarryStocker對DEA效率值的研究,將DEA效率值分為4類,即:強勢效率單位(The RobustlyEfficient Units),相對效率值為1,松弛變量全部為0;邊緣效率單位(The Marginal Efficient Units),相對效率值為1,松弛變量不全部為0;邊緣非效率單位(The Marginal Inefficient Units),單位整體效率值介于1與0.9之間,表示只要在投入產出項稍作調整即可達到效率值為1的水準;明顯非效率單位(The DistinctlyInefficient U-nits),單位整體效率值低于0.9,表示該單位經營效率不佳。
那么就可以看出2011年1月份上市的15家公司中,只有2家為強勢效率單位,其余均為明顯非效率單位。即這15家上市公司的整體融資效率并不高。
五、DEA的分析總結
通過DEA在上市公司融資效率的分析中,我們可以看出DEA分析有著以下的優點:(1)它和傳統的評價方法不一樣,DEA方法可以同時對不同決策單元在不同時期內的產出水平進行綜合評價。(2)DEA方法不需要通過主觀確定各輸入輸出指標的權重,它只是將權重看作是變向量,在分析過程中通過某種原則進行確定。它使得通過DEA方法的出來的結論更加客觀。(3)DEA方法在測量各決策單元的相對有效性的時候,注重的是對每個決策單元進行優化。因此,它得出來的相對效率是其最大值,所得出的權重也是最優的。(4)對于無效的決策單元,DEA方法不僅僅可以指出該決策單元的調整方向,并且還能夠給出具體的調整量。(5)DEA方法的有效前沿面是一種內在生成的參照面,它是由有效決策單元所組成的,因此它更具有參照性和客觀性。(6)DEA方法在測量決策單元的相對有效性的時候,它不需要估計該決策單元的生產函數,因此避免了由于采取了錯誤的生產函數,而得出了錯誤的結論的可能。
但是由于DEA方法其假設和自身方法的原因,同時也存在著如下幾方面的局限性:(1)由于DEA模型的假設前提是在投入盡可能少的情況下,產出越大越好。但是在現實生產中,對于某些情況下的產出,并不是越大越好。例如,在工業生產中的廢水、廢渣、廢氣,這些產出并不是越大越好。(2)當在DEA分析中,對比投入產出指標的數量,如果DMU的數量并不足夠大的時候,會顯著影響DEA模型的辨析能力。為了提高DEA模型的評價功能,有學者認為投入產出指標的數量最好不要超過DMU總量的三分之一。(3)在DEA分析的結果中,只是簡單的將DMU效率分為四個等級,即強勢效率單位、邊緣效率單位、邊緣非效率單位和明顯非效率單位。對于同為DEA有效的DMU來說,DEA模型認為它們一樣的好。很顯然這樣的判斷過于武斷。(4)由于各個投入產出指標的權重是通過DEA模型計算出來的,而且在DEA模型中也沒有對各個權重的取值范圍加以任何限制。因此,在這種情況下,有可能出現對權重分配不切實際的問題。其帶來的結果就有可能是:某項DMU有效,僅僅是因為其某項投入指標的權重過小,或者某項產出指標的權重過大。
[1]魏權齡.數據包絡分析[M],科學出版社,2004.
[2]盧福才.企業融資效率分析[D],北京,中國社會科學院,2000.
[3]陳賢錦.基于DEA的上市公司股權融資效率分析[J],融資研究,2010,(4).
[4]毛世平.技術效率理論及其測度方法[J],農業技術經濟,1998,(3).
(作者單位:內蒙古財經學院)

