艦船剛性阻振質量基座振動特性優化設計

姚熊亮 王強勇 朱 楓 龐福振

哈爾濱工程大學 船舶工程學院，黑龍江 哈爾濱 150001

1 引言

在船體結構上安裝船用機械設備通常借助中間安裝構件——隔振基座，其作用是連接設備與船體結構，承受設備的動靜載荷，傳遞船體與設備之間的相互作用載荷，同時限制和阻抑設備傳遞下來的振動。傳統隔振設計是在設備與基座之間配置彈性支撐或阻尼物質，這屬于柔性隔振。但實際應用中，與動力機械相連的某些設備或結構在運行時往往不允許自身有大的變形，此時采用柔性隔振技術來阻隔振動波的傳遞是不適宜的，而必須研究使用剛性減振技術。在我國某型艦上動力機械設備的隔振中，除采用常規隔振措施來阻抑結構聲振動的傳遞外，還在隔振基座與船體板之間設置了剛性阻振質量來阻抑結構聲振動的傳遞，在實際中取得了良好的隔振效果［1］。

艦船剛性阻振質量基座就是在艦船基座與船體結構連接部位布設剛性阻振質量，由于阻振質量相對船體板而言具有較大的阻抗，從而反射一部分抵達阻振質量的振動波來達到隔離聲振動的目的［2］。因此，剛性阻振質量的布設位置及其截面尺寸對艦船基座的隔振效果非常重要。為了提高艦船剛性阻振質量基座的隔振性能，同時不過度增加基座艙段的總重量，采用結構優化設計方法對基座進行動力學優化便成為必然的選擇。結構優化設計理論和方法經過60多年的飛速發展，目前已逐步應用于工程設計領域。考慮結構強度、固有頻率和動響應約束的結構動力學尺寸、形狀和拓撲優化設計也開始得到應用，但在艦船振動聲學方面的應用還非常薄弱［3～6］。

本文在上述文獻的基礎上，探索完善了艦船剛性阻振質量基座的設計理論和方法，通過引入結構動力學優化設計理論，在滿足艦船基座艙段總重量限制的條件下，建立了剛性阻振質量布設位置及截面尺寸優化設計模型，進行了以基座艙段耐壓殼體振動加速度為目標函數的動力學優化設計，所得結論能為剛性阻振技術在實際基座設計中的應用提供一定的參考。

2 艦船剛性阻振質量基座優化模型描述

優化設計以艦船剛性阻振質量基座中阻振質量的截面尺寸及布設位置為設計變量，采用參數化定義、參數化建模、求解、結果提取及優化變量（設計變量、狀態變量、目標函數）賦值。其目的是在滿足艦船基座艙段總重量限制約束的條件下，基座艙段耐壓殼體平均振動加速度級最小，具體優化分析流程圖如圖1所示。

圖1 優化分析流程圖Fig.1 Optimization analysis flow chart

本文采用的基座艙段模型為有沿軸向均布環肋加強的耐壓殼體，如圖2所示。其具體幾何尺寸為：艙段圓柱部分長度l1＝1.5m，圓臺部分長度l2＝4.8m，圓臺大徑 D＝3.5m，小徑 d＝2.625m，采用外肋加強，肋距 l＝0.600m，殼板厚度t＝0.028m，殼內對稱布置了兩列基座，如圖3所示。

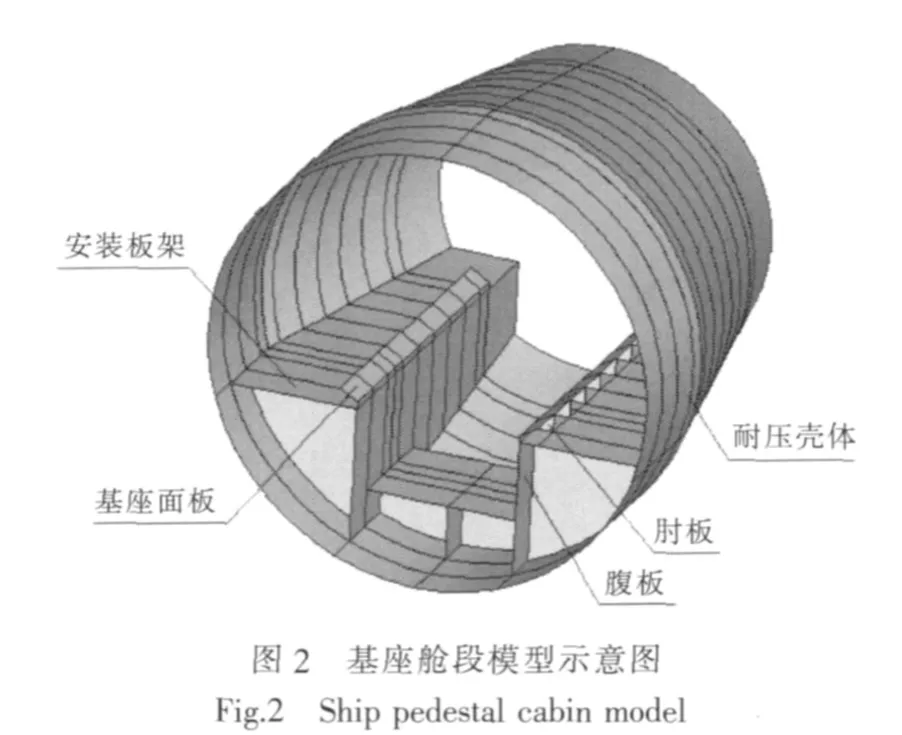
艦船剛性阻振質量基座由基座面板、腹板、肘板、安裝板架及布設在基座腹板上的剛性阻振質量帶組成，如圖4所示。本文所研究的剛性阻振質量基座結構模型具體尺寸如圖5所示。基座面板c＝0.341m，厚度 t1＝0.045 m；腹板 f＝0.110m，厚度 t2＝0.020 m；肘板g＝0.290m，厚度 t3＝0.020 m；安裝板架 k＝0.290m，厚度 t4＝0.020 m。 剛性阻振質量布設在基座腹板上靠近安裝板架處，距離安裝板架e，截面尺寸a×b。整個基座艙段模型的材料參數為：彈性模量E＝205 000 MPa，泊松比μ＝0.3，密度 ρ＝7 800 kg／m3。

對基座結構進行基于頻率響應的動力學優化分析，計算時，將基座艙段前后各沿軸向向外延伸的三檔肋位沿周向施加全約束。基座上設備重75 t，為了簡化計算，將設備重量以質量點的形式均布于基座面板，然后在兩邊基座面板上分別選取12個點作為設備隔振器的安裝點，設備激勵力（垂直于基座面板）通過這24個隔振器安裝點傳遞到基座上并激勵耐壓殼體振動，激勵力幅值為176 N，激勵頻率范圍取10～500 Hz，間隔為10 Hz。

3 剛性阻振質量截面尺寸優化分析

本優化是進行艦船剛性阻振質量基座中剛性阻振質量截面尺寸的優化設計。優化中，保持剛性阻振質量基座中阻振質量布設位置一定，e＝，即剛性阻振質量截面中心與基座腹板高度方向中心重合，以振動加速度作為基座減振效果的評定參數，通過計算基座艙段耐壓殼體平均振動加速度級來對基座隔振效果進行評估，以期得到最佳的剛性阻振質量截面尺寸。

設計變量：剛性阻振質量基座中阻振質量截面參數a＝0.040～0.080m，間隔0.001 m；b＝0.04～ 0.08m，間隔 0.001 m。

狀態變量：剛性阻振質量基座艙段總重量。

目標函數：基座艙段耐壓殼體平均振動加速度級。

為綜合考察在對剛性阻振質量基座中阻振質量截面尺寸進行優化分析時，基座艙段耐壓殼體在10～500 Hz頻段總的振動情況，在耐壓殼體上選取15個典型結構測點，如圖6所示。對這15個結構測點的響應值按下式取平均聲振動級：

其中，Lai為由10～500 Hz頻段上各頻譜分量的加速度響應值轉化的振動加速度級［7］，ai為10～500 Hz頻段上各頻譜分量的加速度響應值；a0為振動加速度基準值，本文取a0＝1×10-6m ／s2。

優化采用零階方法，設置最大迭代次數為50，連續15次不收斂即退出循環。優化結果如表1所示，既有可行解，也有不可行解。圖7和圖8分別給出了優化計算中剛性阻振質量基座艙段總重量和基座艙段耐壓殼體平均振動加速度級的迭代收斂曲線，可以看出，迭代到第9次，結果便已收斂，即 a＝0.072，b＝0.042 的組合為最優組合。在艦船基座中引入剛性阻振質量后，基座艙段總重量由 47.08 t增加為 47.33 t，僅增重 0.53%。

從表1中的數據及圖7、圖8中迭代曲線的變化趨勢基本可以看出，剛性阻振質量基座中阻振質量高度a越大，基座艙段耐壓殼體平均振動加速度級就越小。文獻［8］對剛性阻振質量阻隔簡單板結構中振動波的傳遞特性進行了研究，得出結論：剛性阻振質量的高度對其隔振特性有很大影響，對于某一激勵頻率，對應某一高度的剛性阻振質量無隔振作用，大于這一高度時，隨著高度的增加，阻振質量對振動噪聲的隔離效果越好。這與上述優化結果基本一致，說明動力學優化分析的結果是正確和可信的。

表1 剛性阻振質量截面尺寸優化結果Tab.1 Optimal results of sectional dimensions of rigid vibration isolation mass

4 剛性阻振質量布設位置優化分析

接下來在上文研究的基礎上，保持剛性阻振質量基座中阻振質量截面尺寸一定，a×b＝0.072 m×0.042m，進行剛性阻振質量布設位置優化分析。設計變量取基座中阻振質量下表面與安裝板架的距離 e＝0.010～0.058m，間隔 0.001m，狀態變量和目標函數與剛性阻振質量截面尺寸優化分析相同。

優化方法的設置與截面尺寸優化一致，優化序列如表2所示。圖9給出了優化計算中目標函數的迭代收斂過程，可以看出，目標函數迭代到第7次，結果便已收斂，即SET7為滿足約束條件的最優化結果。

從表2中的數據和圖9中的迭代曲線可以看出，剛性阻振質量基座中阻振質量的最佳布設位置為 e／f＝0.47。 另外，通過優化剛性阻振質量基座中阻振質量的布設位置，基座艙段耐壓殼體平均振動加速度級由 126.23 dB 變為 125.54 dB，降低了0.69 dB，提高了剛性阻振質量的隔振效果。

5 結 論

本文分別以剛性阻振質量截面尺寸和布設位置為設計變量進行了艦船剛性阻振質量基座在基座艙段總重量限制的約束下離散變量的動力學優化，得到了兩種情況下基座艙段耐壓殼體平均振動加速度級隨迭代次數的變化曲線和優化序列。從表和曲線中可以看出，在滿足約束的條件下，剛性阻振質量基座中阻振質量高度a越大，基座艙段耐壓殼體平均振動加速度級就越小，且通過優化分析得到剛性阻振質量最佳截面尺寸和布設位置分別為 a＝0.072，b＝0.042，e／f＝0.47。可見通過優化設計能找到滿足要求的結構，可分析出目標函數隨設計變量的變化趨勢，而且所得優化結果與相關文獻分析結果基本一致，驗證了此優化方法的有效性，為實際工程設計應用提供了一定的參考。

［1］朱石堅，何琳.船舶機械振動控制［M］.北京：國防工業出版社，2003.

［2］阿·斯·尼基福羅夫.船體結構聲學設計 ［M］.謝信，王軻，譯.北京：國防工業出版社，1998.

［3］汪玉，陳國鈞，華宏星.船舶動力裝置雙層隔振系統的優化設計［J］.中國造船，2001，42（1）：45-49.

［4］楊德慶，柳擁軍.薄板減振降噪的拓撲優化設計方法［J］.船舶力學，2003，7（4）：91-96.

［5］楊德慶，郭鳳駿.振級落差約束下齒輪箱基座拓撲構型設計［J］.振動與沖擊，2008，27（6）：173-177.

［6］郭鳳駿，楊德慶.考慮振級落差要求的齒輪箱基座優化設計［J］.船舶工程，2008，30（4）：1-4.

［7］NORTON M P.工程噪聲和振動分析基礎［M］.盛元生，顧偉豪，韓建民，等譯.北京：航空工業出版社，1993.

［8］胡忠平，冷駿.方鋼對艦船結構噪聲的傳播與阻隔機理分析［J］.機電設備，2008，4（1）：44-47.