基于電抗加載的單通道五元多波束掃描天線陣設計方法研究

李戈陽 李 瑞 李維林

1 中國艦船研究設計中心，湖北 武漢 430064 2 海軍裝備部，北京 100071

1 引 言

電子對抗與反對抗［1-2］在現代海戰中是極為重要的組成部分，奪取電子戰的主動權，是取得戰爭勝利的先決條件。美國CODAR公司設計了由3根天線組成的單極子交叉環天線陣，用于超分辨到達方向估計，但最多只能對2個信號到達角方向上形成具有陡峭下降延的峰值增益。類似地，文獻［3］中基于電壓控制的電抗加載多波束掃描陣和文獻［4］設計的HF自適應三元陣列零位天線系統，其自由度皆為2，最多只能在2個干擾來波方向上形成零陷，以抑止2個來向的干擾［5-6］。

在實際信號環境中通常存在多個信號，因此，有必要對緊湊的、能實現多信號到達方向估計的高頻地波雷達天線陣［7-8］進行研究。針對該問題，本文研究設計了一個電抗加載單通道五元多波束掃描圓陣，并結合空間譜估計方法對信號到達方向［9］進行了估計與分析。

2 電抗加載天線陣的矩量法分析

自從1968年哈林頓（Harrington）將矩量法應用于電磁學后，矩量法一直是分析線天線輻射與散射問題的有效工具［10］。 矩量法（Method of Moments，MOM）是一種將線性空間的算子方程轉化為矩陣方程來進行計算的數值方法。本文根據矩量法原理，采用分段正弦基和伽遼金法來計算天線陣各單元的電流分布［11］。

根據矩量法原理，采用分段正弦基和伽遼金法分析天線，設每根振子均勻分為m＋1小段，形成m個元偶極子，振子的全長為2L，共有n根振子。在第1根振子的中心用電壓源V0饋電。則可構造矩陣方程：

在式（1）中，N＝m×n。令加載的阻抗矩陣為［ZL］，即

矩陣［ZL］中對角線上的元素為各天線的加載電值。考慮電抗加載后，新的廣義阻抗矩陣為［12］：

得到每個振子上的電流分布后，即可計算圓陣的基本輻射性能。

上述分析說明，通過改變天線陣中任一振子的電抗加載值即可改變天線陣中各振子的電流分布，從而改變天線陣的整體輻射特性。因此，可以考慮采用調整電抗加載值的方法，盡可能地增加天線陣在期望方向的增益，抑止旁瓣和壓縮波束等。

3 單通道電抗加載五元多波束圓陣的設計

傳統的天線陣實現多波束掃描所采用的方法是加載多組波束形成網絡，通過在不同波束形成的網絡組間進行切換使天線陣方向圖對準不同指定方向，如此循環切換，實現空間多方向來波信號掃描的目的。這種方法存在的問題是［13］：

1）波束形成網絡的實現方法較復雜，多個接收通道處理難以保證各通道的一致性［14］，這將會使利用各通道數據生成的相關矩陣產生畸變，從而導致算法失靈和系統誤判，嚴重的，甚至會引起系統癱瘓。另外，要加載若干組不同的波束形成網絡，調試和實現也會非常困難。

2）加載多組波束形成網絡使加載電磁元件的個數大大增多，將影響天線間的耦合程度和天線陣的增益大小。

3）若多組波束形成網絡中有一組設計不當或出現故障，便難以進行故障排查工作。

4）由于需要多路接收、多路饋電和網絡匹配，這將增加天線系統的體積、復雜度與成本，從而導致系統可靠性降低。

與傳統多波束掃描天線陣相比，本文所設計的多波束掃描圓陣只需一個接收通道，且不需要復雜的波束形成網絡。只需對中心振子進行饋電，對其它寄生振子進行電抗加載，即可實現空間任意方向的波束掃描。

基于該原理，設計了如圖1所示的單通道電抗加載五元多波束圓陣。

設天線陣半徑為3／8λ，工作頻率為8 MHz，令波束掃描的角方向 φ 分別對準 0°、90°、180°、270°和全向。通過計算得到波束對準各方向時，編號1～5的天線電抗加載值序列為：

各寄生天線上有一個切換開關用來選擇不同的電抗加載值，如圖2所示。

結合圖1與圖2可以看出，電抗加載單通道五元多波束圓陣天線系統由以下3部分組成：

1）中心饋電振子和圓周的無源寄生振子；

2）一個與中心振子相連的接收通道；

3）分別加載于4個圓周振子上的電抗加載網絡。

當各振子的切換開關同時在X1～X5間進行切換時，天線陣波束掃描的φ角方向分別為0°、90°、180°、270°和全向掃描，如圖 3 所示。

從圖3中可以看出，電抗加載單通道五元天線陣能順利地完成空間波束掃描，結合空間譜估計方法對通道輸出信號進行分析，即可實現信號到達角的估計。下面將在不同信號個數、不同信噪比、不同采樣點與信號角間距的情況下，檢驗天線陣的性能。

4 仿真分析

基于MUSIC算法［15-16］，采用分時采樣的方法對五元波束掃描天線陣進行分析計算，設來波方向為φ＝60°，取512個采樣點，信噪比為20 dB。通過計算得到該信號的到達方向估計，如圖4所示。

在圖4中，60°方向有一尖峰，表明掃描到該方向有一到達信號。可以看出，計算得出了信號到達方向的準確估計。

在信噪比為20 dB，采樣點數為512點的前提下，分別考察2個和3個到達信號方向的估計。設2個信號到達角的角度間隔為15°，3個信號到達角的角度間隔為20°，計算結果如圖5所示。

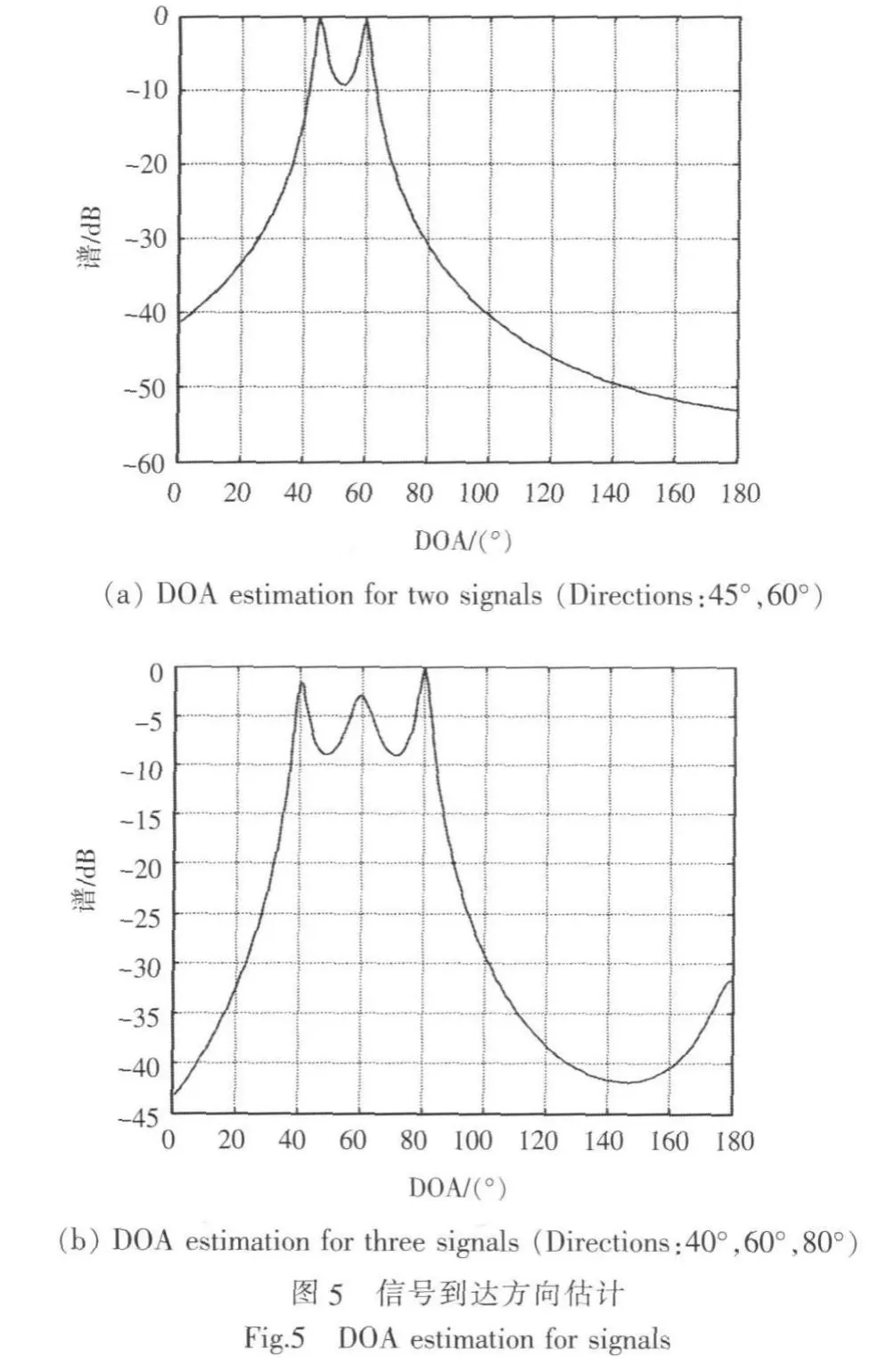
以上結果說明，算法可以對2個和3個信號來向進行較精確的估計。在此基礎上，分別考查信噪比和采樣點數對多信號估計結果的影響。

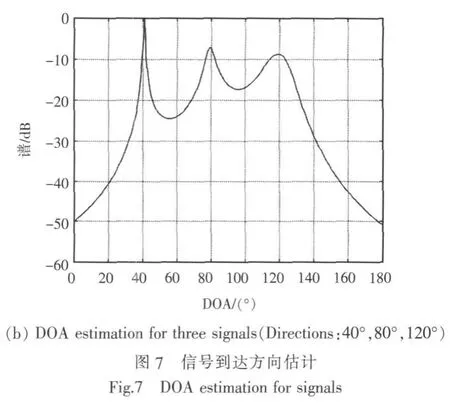
圖6給出了信噪比僅為10 dB，采樣點數為512點時，天線陣對2個和3個來波信號的DOA估計。由圖6可知，當信噪比降低到10 dB時，算法仍能分辨2個以上的信號，但與圖5相比，其只能分辨角間距較大的信號，且譜估計的結果不能呈現很尖銳的峰值。這說明信噪比的減小使天線陣對2個以上信號DOA估計的性能有所下降。此時，保持信噪比為10 dB不變，增加采樣點數至1 024點，再次估計2個和3個來波信號DOA，其結果如圖7所示。

由圖5～圖7可以看出，在信噪比較小的情況下（圖7，信噪比為10 dB），增大采樣點數已不能明顯改善算法對多信號估計的結果。而對比圖5和圖6則發現，信噪比的提高可明顯改善算法結果，如估計譜圖的峰值更陡峭、能分辨更小角間距的信號等。因此，要想獲得更佳的估計結果，應著重考慮提高信號的信噪比。

由于n元天線陣最多可分辨n-1個信號，所以設計的五元天線陣應能分辨4個來波信號。設信噪比為35 dB，采樣點數為1 024點，4個信號到達角的角度間隔為30°。通過計算得到這4個信號的DOA估計如圖8所示。

對計算結果進行分析可知，當信號的個數增多時，要靠增大信號角間距，提高信噪比，增加采樣點數的方法來獲得更優的DOA估計結果。在信號來波方向估計精度上，角度誤差在±3°以內。對定向信號接收而言，完全能滿足工程應用需要。

5 結 論

本文以矩量法為基礎，采用電抗加載的思想設計了單通道多波束掃描五元高頻地波雷達圓形陣，并結合MUSIC算法進一步對信號DOA進行了估計。仿真結果表明，該圓陣能自適應地進行小于5個信號DOA的較精確估計，信號的分辨效果受信噪比、采樣點數與信號間角間距的影響。但當來波信號為5個甚至更多時，天線陣需要增加陣元以滿足DOA估計的需求。此時，在信號角間距、信噪比與采樣點數一定的情況下，為獲得滿足實際應用需求的角分辨效果，需要對MUSIC算法進行進一步的優化，同時，作為高頻地波雷達天線陣，陣列的小型化設計也至關重要。

［1］黎鐵兵，黃高明，饒德虎.艦艇編隊電子對抗系統仿真研究［J］.計算機仿真，2009，26（11）：10-13，24.

［2］李志成.艦載雷達電子對抗技術概述 ［J］.艦船電子對抗，2005，28（2）：6-9.

［3］沈潔，郭輝萍，劉學觀.一種三單元新型寬波束掃描電控無源陣列天線 ［J］.中國電子科學研究院學報，2009，4（2）：211-215.

［4］陳健，李建東，裴昌幸，等.HF零位天線系統及其算法［J］.電波科學學報，2003，18（3）：286-289.

［5］陳健，裴昌幸，曾興雯，等.一種VHF自適應零位天線系統［J］.西安電子科級大學學報（自然科學版），2002，29（5）：660-663.

［6］胡航，劉偉會，吳群，等.一種有效的子陣級波束掃描旁瓣抑制方法［J］.電波科學學報，2009，24（4）：593-597，666.

［7］高火濤，楊子杰，李杰，等.岸基遠程高頻表面波雷達小型寬帶天線系統的設計 ［J］.電子與信息學報，2004，26（1）：112-117.

［8］周濤，施春榮，戎信云，等.數字化高頻地波雷達系統優化設計［J］.雷達與對抗，2008（4）：6-8，31.

［9］張平芳，程韌.基于均勻圓陣的相干信源DOA估計算法研究［J］.電子工程，2008（1）：1-4.

［10］HARRINGTON R F.Field computation by moment methods［M］.New York：IEEE Press，1968.

［11］HARRINGTON R F.計算電磁場的矩量法［M］.王爾杰，肖良勇，譯.北京：國防工業出版社，1981.

［12］牛俊偉.電抗加載定向天線陣的輻射特性研究［D］.西安：西安電子科技大學碩士學位論文，2001.

［13］岳安軍，裴昌幸，葛建華.一種時分單通道自適應天線的研究［J］.電波科學學報，2005，20（2）：175-179.

［14］柳超，劉其中，梁玉軍，等.艦用短波寬帶鞭狀天線研究［J］.電波科學學報，2006，21（6）：955-958.

［15］TUNG T L，YAO K，CHEN D，et al.Source localization and spatial filtering using wideband MUSIC and maximum power beam forming for multimedia applications［C］//IEEE Workshop on Signal Processing Systems，SiPS：Design and Implementation，Taipei，1999：625-634.

［16］ASTELY D，OTTERSTEN B.The effects of local scattering on direction of arrival estimation with MUSIC ［J］.IEEE Transactions on Signal Processing，1999，47 （12）：3220-3234.