滾動軸承的實調制細化包絡譜診斷方法研究

黃國樑，周玉彬，郭 華，時獻江

（1.哈爾濱大東人造板設備制造有限公司，黑龍江 哈爾濱 150040；2.哈爾濱理工大學機械動力工程學院，黑龍江 哈爾濱 150080）

0 引 言

滾動軸承的振動信號往往具有調制信號特征，此時，軸承的部件共振頻率成分為信號的載波頻率，故障頻率為調制頻率。通常載波信號頻率較高，且遠離一般零部件的故障振動頻率范圍，可以利用高頻段提取軸承的故障信息，避開低頻段其他振動能量較大信號的干擾，這就是常見的滾動軸承故障診斷的共振解調法。

共振解調法的主要思想是去掉信號中無用的部件共振頻率成分，僅提取有用的調制故障頻率成分，這可以用Hilbert變換求包絡譜的方法來實現。但是，由于軸承部件本身的共振頻率較高，通常需要采用較高的采樣頻率，因此直接對原始信號進行包絡分析往往會由于頻譜的分辨率過低而無法識別故障特征。為此，很多學者提出了細化包絡譜的概念，常見的有采用Hilbert變換+細化譜實現的數字細化包絡方法[1-3]，采用小波變換的細化包絡算法等[4]。該文根據通信信號中的調制與解調原理，參照復調制細化譜的復調制移頻原理，并利用Hilbert變換求包絡譜技術，實現了一種實數調制+Hilbert變換求包絡的新細化包絡譜算法，并在Matlab環境下實現，最后給出了該算法在滾動軸承故障診斷中的應用。

1 復調制移頻原理

采用復調制的移頻過程如圖1所示。其基本原理是先將感興趣的某一高頻頻段平移至低頻段，這相當于對原始信號x（t）進行復調制，即

式中：f0——欲細化頻段的中心頻率。

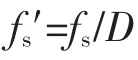
2 實調制移頻算法原理

時域離散化會引起信號頻譜的周期性變化，即一個待分析的頻段應是一個正負頻率對稱的，采用復調制法的結果卻會破壞這種對稱結構（如圖1所示）。當欲細化分析頻段的中心頻率為f0，寬度為B時，可以采用圖2所示的移頻過程，即正頻率部分左移f0-B/2，負頻率部分右移f0-B/2，這個移動過程在頻域的數學表達式為

其在時域中的表達式為

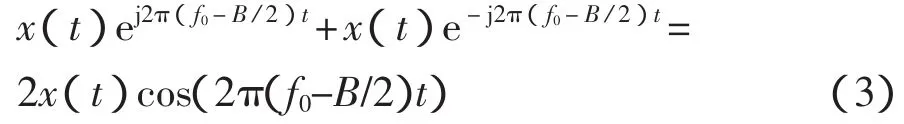
也就是說，對原始信號x（t）乘以2cos（2π（f0-B/2）t）就可以實現圖2所示的移頻過程，相對于復調制，稱為實調制，其移頻計算流程如圖3所示。由于實調制后的信號頻譜保持了原來的正負頻率成分對稱關系，所以調制結果仍為實信號，這為后續采用Hilbert變換求包絡譜提供了可能。

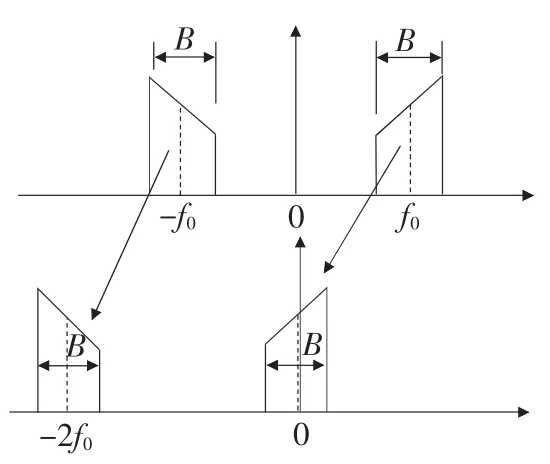
圖1 復調制方式下的移頻過程示意圖

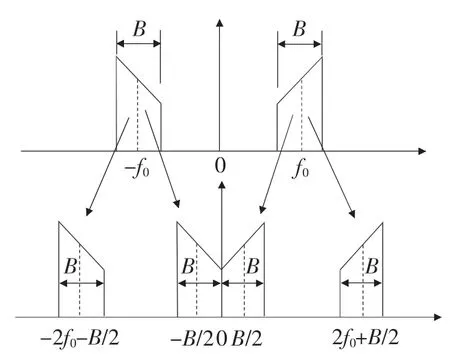
圖2 實調制方式下的移頻過程示意圖

圖3 實調制移頻算法流程圖

3 Hilbert變換及包絡譜算法

3.1 基本原理

設x（t）為一個實時域信號，其Hilbert變換定義為

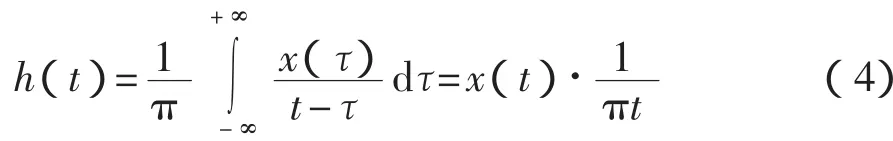
則原始信號 x（t）和它的 Hilbert變換信號 h（t）可以構成一個新的解析信號xa（t）

其幅值

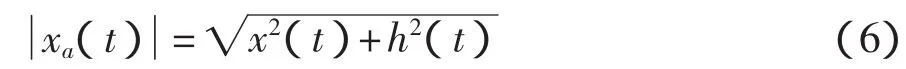
便為原始信號x（t）的幅值解調信號[6]。

根據傅里葉變換原理，信號x（t）的Hilbert變換在頻域中的表達式為

可見，Hilbert變換相當于一個幅頻特性為1的全通濾波器，信號x（t）通過Hilbert變換后，幅值不變，僅僅是負頻率做了+90°相移，正頻率做了-90°相移。

3.2 采用Hilbert變換的信號解調計算流程

（1）將待分析信號x（n）通過傅里葉變換得到它的頻域函數X（k）。

（2）根據式（7），將正頻率相移-90°，負頻率相移90°，得到經過相移的頻域函數X′（k）。

（3）對X′（k）進行傅里葉逆變換得到時域信號x′（n），它即是x（n）的Hilbert變換h（n）。

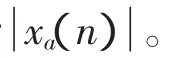
圖4 采用Hilbert變換的包絡譜算法流程圖

4 實調制細化包絡譜求解方法

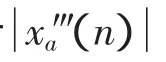
圖5 實調制細化包絡譜算法流程圖

根據3.2知，采用Hilbert求包絡譜過程需要進行3次FFT運算，計算量較大。實調制移頻方法是將Hilbert變換求包絡譜過程放在了實調制和重新采樣之后，這樣，Hilbert變換過程僅針對重抽后的N點信號進行計算，而不是原始的D·N點信號，所以計算量大大減少，提高了細化包絡譜的計算速度。這是和其他細化包絡譜求解方法的顯著區別點之一。

5 實調制細化包絡譜在滾動故障診斷中應用

將該方法應用在滾動軸承故障診斷中，進行了滾動軸承故障診斷的實驗驗證。實驗選用308軸承，通過在軸承外圈滾道上人工鉆坑模擬滾動軸承的外圈故障，采用加速度傳感器測取軸承的徑向振動信號。試驗時軸承轉速為1000r/min，信號采樣頻率為20 kHz，基本采樣點數N=1 024，細化分析時采樣點數為5 120，細化倍數D=5，采樣時模擬抗混濾波器的截止頻率為3kHz，包絡分析時帶通濾波器的帶通范圍為4~10 kHz。分別應用普通分辨率的FFT頻譜、Hilbert包絡譜及實調制細化包絡算法對實驗結果進行了分析與比較。

圖6為軸承外圈故障時的振動加速度時域波形，圖7為帶通濾波后的普通分辨率幅值譜，可見在7kHz左右有一個共振峰，且有明顯的等頻率間隔的邊帶成分。由于頻譜分辨率較低，難于精確地識別邊帶成份。

圖6 外圈故障時的振動加速度時域波形

圖7 帶通濾波后的原始信號頻譜

圖8 外圈故障時的普通分辨率Hilbert包絡譜

圖8為軸承外圈故障，采樣點數N=1 024時的Hilbert變換包絡譜。可見，由于頻率分辨率較低，解調后故障特征頻率信號均集中于低頻處，譜圖中實際計算的故障特征頻率為35.28 Hz，與理論計算故障頻率49.23Hz（308軸承，轉速為 1000r/min）相差較大。圖9為細化倍數D=5時的實調制細化包絡譜，已經可以清晰地分辨出滾動軸承外圈故障的特征頻率（實測為47.38 Hz）及其倍頻，而且與理論計算值非常接近。另外，與圖8比較，圖9中除故障特征頻率外，其他干擾成分也大大減少，主要原因在于調制移頻過程實際上又相當增加了一次共振解調過程。即用一個和部件共振頻率成分接近的信號與原始信號相乘，會由于共振作用放大共振頻率及其調制的故障特征頻率，壓縮其他無關的頻率成分，能夠提高信號分析的信噪比，這也是實調制移頻細化譜應用于滾動軸承故障診斷的優點之一。

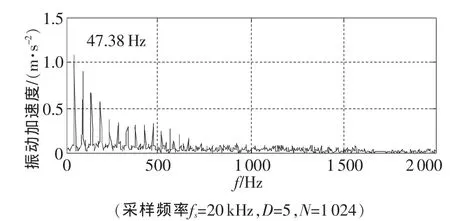
圖9 外圈故障時的實調制細化包絡譜

6 結束語

采用實調制頻移技術結合Hilbert變換，可以使細化包絡譜的計算效率大大提高，而且由于實調制過程本身的二次共振解調作用，還可以放大部件的共振頻率及其調制的故障頻率成分，壓縮其他無關的頻率成分，提高信號分析的信噪比。

在滾動軸承的細化包絡譜中，由于將2個邊帶（故障頻率）合為一根譜線，有信息凝合的作用，克服了原始信號頻譜中邊帶不對稱問題。由于能夠剔除無用的部件共振頻率成分，得到的細化包絡譜能更精細、準確地反映故障特征頻率的變化，說明該方法具有實際應用價值。

[1]何景光，吳雅，皮鈞，等.一種包絡譜細化的新方法及其在故障診斷中的應用[J].華中理工大學學報，1993，21（1）：95-99.

[2]皮鈞，王建軍.包絡譜細化的新方法及其在齒輪故障診斷中的應用[J].拖拉機與農用運輸車，2003（5）：10-12.

[3]杜秋華，楊曙年.細化包絡分析在滾動軸承缺陷診斷中的應用[J].軸承，2004（3）：31-34.

[4]萬書亭，呂路勇.基于小波包和細化包絡分析的滾動軸承故障診斷方法研究[J].中國工程機械學報，2008，6（3）：349-353.