邏輯學在《數學分析》教學中的應用
何先平,宋述剛
(長江大學信息與數學學院,湖北 荊州 434023)
邏輯學在《數學分析》教學中的應用
何先平,宋述剛
(長江大學信息與數學學院,湖北 荊州 434023)
在《數學分析》教學中,運用邏輯學的原理與方法,闡明《數學分析》的分析與綜合方法,揭示極限等重要概念中的性質判斷的定義結構,有助于突出教學重點,分解教學難點,使學生深入理解和掌握《數學分析》的基本概念與思想方法,從而提高《數學分析》的教學質量。
數學分析;邏輯學原理;分析;綜合
在科學發展的初期,數學被包含在哲學的母體之中。邏輯學是研究思維的邏輯形式、基本規律與方法的學科,它與數學有著十分密切的關系。在它的發展過程中,不斷借用數學的思想方法,反過來又促進數學的發展。《數學分析》是大學相關專業十分重要的基礎課程,蘊含著豐富的邏輯思維原理與方法。《數學分析》充分運用了分析與綜合的邏輯思維方法,其基本概念——極限的定義,被稱之為典型的分析語言,即是分析與綜合的體現,其中包含了一些全稱判斷與特稱判斷,由此構成一個復合判斷。極限的概念與方法,貫穿于《數學分析》的始終,既是教學的重點,也是教學的難點,其教學歷來受到特別的重視。因此,在《數學分析》教學中,運用邏輯學的原理與方法,對提高教學質量有著非常重要的意義。
1 分析與綜合
分析法與綜合法則是常用的普通邏輯思維方法。分析法就是把復雜的事物或過程分解成各個部分、局部或階段,然后用孤立、靜止的觀點逐個對其研究,從而得出事物的微觀性質;而綜合法則是把事物的各個部分或階段的微觀性質有機整合在一起,把握事物的整體、宏觀性質。通常人們往往將這兩者先后結合起來,達到認識事物的目的。概念、判斷、推理是思維的基本形式,因而數學概念就是教學中首先要注重的對象。《數學分析》的基本概念,例如極限、微分、積分的定義都采用了分析與綜合的方法。下面以極限與定積分的概念為例說明。
|an-a|<0.1 |an-a|<0.01 |an-a|<0.002 …
對于上述每個變化階段,用孤立、靜止的觀點研究它們,所得條件是自變量n必須大于某個正整數。這樣的變化階段有很多很多,它們具有上述類似的特征,運用邏輯量詞符號,將其綜合、概括起來即為:
?ε>0,?正整數N,當n>N時,都有|an-a|<ε
的近似值的極限值即為它的精確值。上述過程中的分割、近似即為分析,而作和、取極限則為綜合,定積分的概念是分析與綜合相結合的完美范例。
2 判斷與否定判斷
判斷是對思維對象有所斷定(即肯定或否定)的思維形式。數學中的判斷大量存在于數學的概念與推理之中。在《數學分析》中,很多判斷屬于性質判斷,即斷定對象具有或者不具有某種性質的判斷。如:①函數f(x)在區間(a,b)可導;②函數f(x)在區間[a,b]不可積。
性質判斷按對象的數量劃分,可分為單稱判斷、全稱判斷和特稱判斷;按性質劃分,又可分為肯定判斷與否定判斷。否定一個全稱判斷,須用特稱判斷,而否定一個特稱判斷,則須用全稱判斷。
《數學分析》大多數基本概念的定義由全稱判斷和特稱判斷構成,如極限、上(下)確界、有(無)界函數、微分、積分等。這些概念都是教學的重點與難點。特別是教學之初就涉及到的極限概念,學生對其正概念,尤其是對其負概念中的“ε-N語言”、“ε-δ語言”的理解和掌握容易產生障礙,究其原因,筆者認為是教學中缺乏邏輯學的指導。
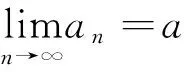
?ε>0,?正整數N,當n>N時,都有|an-a|<ε
這是一個復合判斷。其中?ε>0…引導一個全稱肯定判斷,而這個判斷之中,又包含一個特稱肯定判斷:?正整數N…,一個全稱判斷?n>N…。
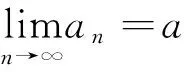
?ε0>0,?正整數N,?n0>N,使得|an0-a|≥ε0
同理,數列{an}發散的定義為:
?a∈R,?ε0>0,?正整數N, ?n0>N,使得|an0-a|≥ε0
類似地,可以討論各種類型的函數極限的定義及其否定形式。
此外,在邏輯推理(例如反證法)中,也經常涉及到全稱判斷和特稱判斷及其否定。
3 結 語
除了上面提到的邏輯學原理與方法以外,《數學分析》還大量運用了演繹推理、歸納推理、類比推理等邏輯推理論證方法與普通邏輯的基本規律,如同一律、矛盾律、排中律和充足理由律。學習與掌握一定的邏輯學知識,不僅可以促進數學的學習,而且可以指導數學的教學。
[1]華東師范大學數學系.數學分析[M]. 第3版.北京:高等教育出版社,2001.
[2] 陳紀修.數學分析[M].北京:高等教育出版社,2002.
[3] 吳家國.普通邏輯原理[M]. 北京:高等教育出版社,1994.
[4] 吳家國.普通邏輯述評[M].上海:上海人民出版社,1990.
[5] 宋述剛,陳忠.微積分理論中的辯證法規律與辯證思維方法[J].長江大學學報(自然科學版),2005,2 (10):385-386.
[6] 屈婉玲,耿素云,張立昂.離散數學[M].北京:清華大學出版社,2005.
[編輯] 洪云飛
10.3969/j.issn.1673-1409.2011.02.047
N4
A
1673-1409(2011)02-0135-02
2010-12-24
何先平(1965-),男,1985年大學畢業,碩士,副教授,現主要從事數理統計方面的教學與研究工作;E-mail:hexp@yangtzeu.edu.cn。

