基于Fisher判別準則的沉積環(huán)境判別與分類方法

董文娟，朱遠鑫，萬明剛

(長江大學信息與數學學院，湖北 荊州 434023)

基于Fisher判別準則的沉積環(huán)境判別與分類方法

董文娟，朱遠鑫，萬明剛

(長江大學信息與數學學院，湖北 荊州 434023)

基于Fisher判別準則建立了沉積環(huán)境判別與分類的Fisher判別分析模型。模型選用粒度的平均粒徑、標準偏差、偏差以及峰值等4個指標作為判別因子，利用方差分析的思想選擇判別系數建立相應的判別函數，以該函數計算待判樣品的Fisher判別函數值，以最大值對應的總體作為樣品的歸屬。判別結果表明，所建立的沉積環(huán)境判別與分類的Fisher判別模型具有一定的實用價值。

粒度；沉積環(huán)境；分類；Fisher判別分析

沉積物粒度參數的變化受搬運介質、搬運方式、沉積環(huán)境和氣候等因素控制，因此，沉積物粒度分析對揭示氣候變化和環(huán)境的演變具有重要意義。粒度參數平均粒徑、標準偏差、偏差、峰值是沉積物粒度4個重要參數。不同粒度組分的形成與搬運與沉積環(huán)境密切相關，處理、分析粒度數據可以進一步確定沉積環(huán)境，這對于現(xiàn)代沉積學的研究，乃至古代沉積物的沉積環(huán)境分析無疑都具有重要的理論和現(xiàn)實意義。

文獻[1]給出了一種單樣品粒度分布表征方法——粒度母體分解圖;文獻[2]通過測試分析發(fā)現(xiàn)沉積巖粒度中值分布、泥質含量、分選性等是影響油藏巖石滲透能力的重要因素，正態(tài)分布能較好地描述低滲透砂巖油藏中沉積物的粒度分布特征;文獻[3]根據數理統(tǒng)計方法對粒度參數進行無偏估計，使之較以往參數估計更加符合無系統(tǒng)誤差的評選標準，并利用這一方法對長樂東部海岸的風沙進行了系統(tǒng)的粒度參數分析;文獻[4]對典型穩(wěn)定湖相沉積物和典型風成黃土粒度參數進行定量化分析，然后利用多元判別分析的Fisher準則建立了湖相與風成沉積物2種沉積相的判別函數; 文獻[5]以粒度參數為輸入變量，設計了沉積環(huán)境判別與分類的神經網絡模型。

下面，筆者將判別分析理論應用于沉積環(huán)境的綜合評判中，建立沉積環(huán)境判別與分類的Fisher判別分析模型。

1 Fisher判別分析

1.1Fisher判別分析的基本思想

判別分析的基本思想，一般是將高維的數據點，利用投影映射到低維空間上，從而方便進行研究。Fisher判別準則是利用方差分析方法對k個總體G1,G2,…,Gk中抽取具有p個指標的樣本數據構造判別函數：R(x)=c1x1+…+cpxp=cTx，其中系數c=(c1,…,cp)的確定原則是使得每個組內的離差最小，最后利用所得的判別函數對待測的樣品進行判別。

1.2Fisher判別分析數學模型

設有k個總體G1,…,Gk，從中抽取樣本數分別為n1,…,nk的樣本，令n=n1+…+nk，其中每個樣品具有p個指標。假設判別函數為：

R(x)=c1x1+…+cpxp=cTxc=(c1,…,cp)Tx=(x1,…,xp)T

(1)

不妨記：

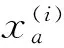
A=cTμiB=cTsic

(2)

Fisher判別準則就是利用方差分析的思想來選取判別系數組成的向量c，使得：

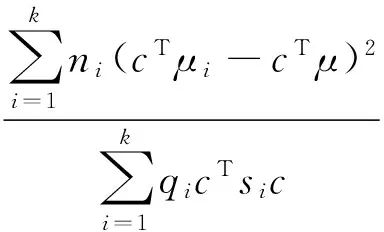
(3)

達到最大，其中qi為正的加權系數，一般取(qi=ni-1)；E，F(xiàn)分別為組間和組內離差平方和：

(4)

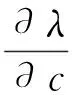
地基沉降的原因主要可以分成2方面：一方面是內部原因，即地基本身就存在不穩(wěn)定性，例如，陜西地區(qū)的土壤類型是黃土，就會更加容易發(fā)生沉降；另一方面就是外部原因，在外部存在著過于強大的附加壓力，超過了地基所能負荷的最大限度，從而使得地基發(fā)生變形，導致地基基礎下沉。

Ec=λFc

(5)

由代數知識可知，該式非零的特征根的個數m不超過min(k-1,p)；因為E為非負定，則非零特征根必為正根，有λ1≥λ2≥…≥λm>0。則可以構造m個判別函數：

Rl(x)=c(l)xl=1,…,m

(6)

1.3Fisher判別準則及檢驗

采取加權法和不加權法對待測樣本x(x1,x2,…,xp)T進行歸類。

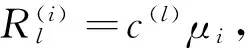
不加權法：

(6)

加權法：

(7)

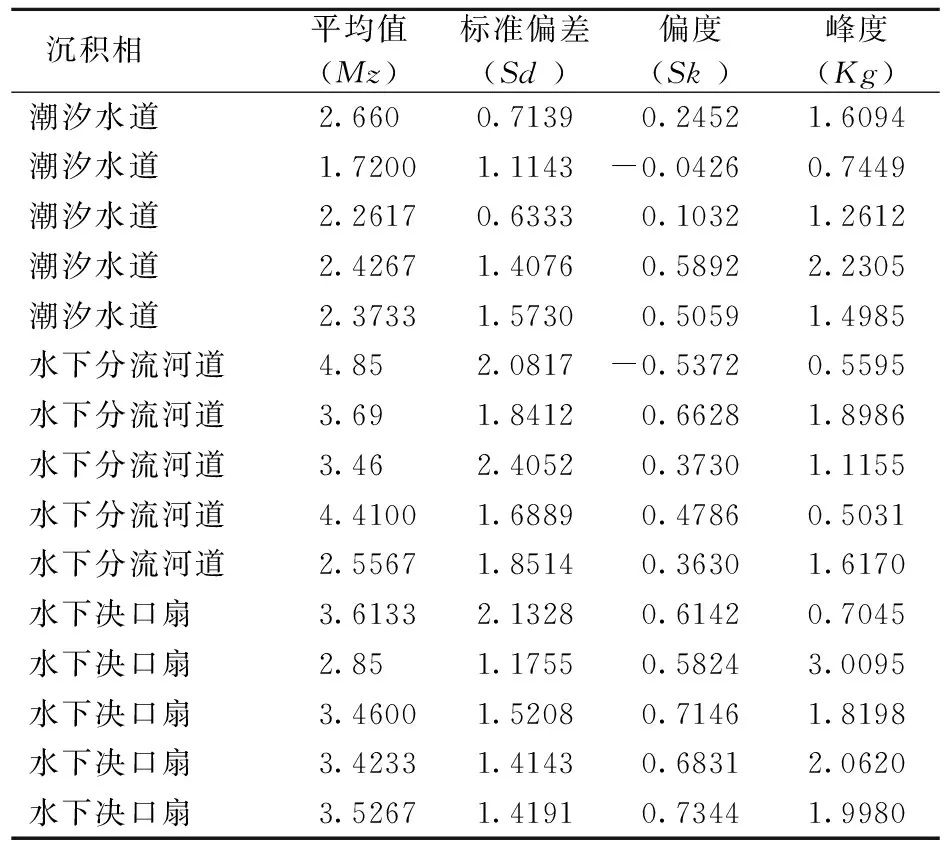
表1 3種沉積環(huán)境的粒度樣本數據

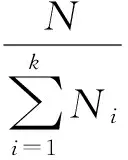
(8)

2 實例分析

珠江口盆地某凹陷是晚新生代古珠江三角洲-濱岸沉積體系形成、發(fā)育及演化的主要場所。在對該凹陷某區(qū)域進行沉積微相劃分時進行了大量的粒度試驗，得到了一系列與沉積微相對應的粒度數據，取其中15個樣本作為訓練樣本，建立Fisher判別函數。其具體樣本數據見表1。

由表1可知，k=3,p=4,i=1,2,3，n=n1+n2+n3=15。

1)計算各判別變量的均值：

μ1=[2.2895,1.0884,0.2809,1.4689]μ2=[3.7933,1.9737,0.2680,1.1387]

μ3=[3.3747,1.5325,0.6657,1.8988]

2)計算各判別樣本的方差：

3)計算組間和組內離差陣:

最后得到判別函數為：

R(x)=0.4296x1+0.5660x2+0.0519x3+0.227

利用上述判別函數對其余60個粒度參數進行判別分析，其判別結果見表2。

表2 60個樣本的識別結果

由表2可知，所建立的沉積環(huán)境判別與分類的Fisher判別模型整體誤判率為23.3%，具有一定的實用價值。

3 結 語

結合多元統(tǒng)計數學知識，以Fisher判別分析方法建立沉積環(huán)境綜合評判的數學模型，為沉積環(huán)境的判別與分類提供了數量化與定量化的途徑。值得指出的是在上述實例中除潮汐水道的判別率較高以外，其余2種沉積環(huán)境的判別率較低。出現(xiàn)整體判別率不高的原因主要在于基于Fisher準則的判別分析法是線性判別，產生的誤差較大，適合兩組間的判別。對于多組沉積環(huán)境的判別，可以嘗試采取Bayesian判別分析法。

[1]曲政.沉積物粒度數據表征方法的研究[J].中國粉體技術, 2001,7(4):24-31.

[2]薛太清.低滲透砂巖油藏沉積物粒度分布特征研究[J].沉積學報, 2006, 24(3):414-418.

[3]楊銳，雷懷彥，劉建輝,等.沉積物粒度參數的無偏估計及其在長樂海岸的應用[J].海洋地質動態(tài), 2007,23(10):33-36.

[4]張平，宋春暉，楊用彪，等.穩(wěn)定湖相沉積物和風成黃土粒度判別函數的建立及其意義[J].沉積學報, 2008,26(3):501-507.

[5]方志江，曲政.基于粒度數據的沉積環(huán)境自動識別方法的研究[J].煤, 1999,3:60-63.

[6]高惠璇.應用多元統(tǒng)計分析[M].北京: 北京大學出版社, 2005.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.05.002

TE19

A

1673-1409(2011)05-0005-03