師生課堂交流中的有效評價引導
——“直線與圓位置關系”復習課教學案例片斷分析

●

(海鹽縣教研室 浙江海鹽 314300)

師生課堂交流中的有效評價引導
——“直線與圓位置關系”復習課教學案例片斷分析

●沈順良

(海鹽縣教研室 浙江海鹽 314300)

師生交流是課堂教學的重要方式.師生數學交流是指在數學教學中，運用數學語言、數學思想方法，接受和表達對數學知識的認識、感受及體驗的一種活動.它能夠加強對數學的理解，鼓勵學生積極參與教學活動，包括思維的參與和行為的參與.課程標準在教學建議中指出，教師要創設適當的問題情境，鼓勵學生發現數學的規律和問題解決的途徑，使他們經歷知識形成的過程.評價應貫穿于數學學習的全過程，有利于數學教與學活動過程的調控.師生課堂的交流能呈現出學生的探索、想法，也能暴露出其思考中存在的問題，教師有效的評價能針對性地引導思維、解決問題并滲透思想方法.下面筆者以“直線與圓位置關系”復習課為例就教師的有效評價引導作簡要的分析.

1 前后方法的比較評價中激活解析幾何思想

師：如何判定直線與圓的位置關系？

生1：通過圓心到直線的距離與圓半徑的大小比較.

生2：解直線與圓聯立的方程組，轉化為一元二次方程的判別式來判斷.

師：這2種方法有什么共同特點？

生3：它們都是將直線與圓的位置關系這一幾何問題轉化為代數方法來解決的，只是前面的方法是利用圓的幾何特征先簡化再用代數方法的.

師：對.它們都體現了運用代數方法解決幾何問題的解析幾何思想，那么哪種方法比較好？

生4：第1種方法好，只要計算圓心到直線的距離即可與半徑比較大小.

生5：第2種方法好，因為第2種方法也適用于后面的直線與其他曲線的位置關系的.

師：都有道理.第2種方法是一般方法，可適用于直線與一般圓錐曲線的位置判別;第1種方法只適用于圓，因為它是利用圓的幾何特征得到的.

例1直線x-y+1=0與圓x2+y2=4的位置關系如何？

生6：畫個圖就可以知道.

師：看圖說話嗎？做大題不可以用，那應該怎么判斷呢？

生7：用圓心到直線的距離和半徑作比較來解決.

師：若變式為：直線x-y+m=0與圓x2+y2=4相交，求m的取值范圍？若直線與圓相離呢？

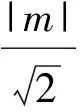
評析獨立思考是數學學習的基本特點之一，教師的評價引導應關注學生善于思考并不斷地改進思考的方法與過程.不同解題方案的交流可以讓學生更多地參與解題思路的探索，也可使學生養成從不同角度思考問題的習慣.在上述教學片斷中，教師通過引導學生對2種方法的異同開展比較評價，突出了知識復習中的解析幾何思想.若能從2條直線的位置關系判斷加以類比，同樣得到2種方法(通過直線方程的斜率比較、解2條直線方程的方程組)，其中前一種方法同樣是先將幾何條件轉化為傾斜程度的關系，再用斜率這一方程中的代數形式來解決，則更有效.2種方法都體現著解析幾何思想，前一種適用于特殊的圓(直線)圖形，后一種適用于一般幾何圖形.

例1中學生回答的方法應該是可行的.它是在坐標系下畫出圖形(根據坐標)，再根據圖形的直觀性直接判斷得到的.對于大題的解答過程來說，只要增加一些說明即可.

2 解題過程的歸納評價中整體把握

例2求過圓x2+y2=1上一點(a,b)的切線方程.

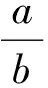
師：你能化簡嗎？

生8：可以.ax+by=a2+b2，即ax+by=1.

師：這樣的過程和結果對不對？

生9：斜率不存在的情況沒有考慮.

師：那么該如何解決？

生9：再一一找出來，得到x=±1，y=±1.

師：那得到的特殊情形在方程ax+by=1中能統一嗎？

生9：將其代入可知是滿足的.

師：對，因此所求切線方程為ax+by=1，還要考慮是否遺漏特殊的情形.

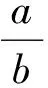
3 對學生錯誤的根源評價加深印象

例3點(a,b)在圓x2+y2=1內，直線ax+by=1與圓的位置關系如何？

生10：這兒的直線和圓是相切的.

師：為何？你怎么想的？

生10：因為直線方程ax+by=1與上面的切線方程相似.

師：上面的切線方程有什么條件？與此有什么不同？

生11：不同的是點(a,b)不在圓上的，上面的結論也不能運用了.

生12：我覺得這兒的直線與圓是相交的關系.

師：能說說你的理由嗎？

生12：因為點(a,b)在圓x2+y2=1內的.

師：點(a,b)是在圓x2+y2=1內的，可直線ax+by=1經過點(a,b)嗎？

生12：將(a,b)代入得a2+b2=1.因為點(a,b)是在圓x2+y2=1內的，所以不滿足條件，因此直線ax+by=1是不經過點(a,b)的.

師：如何判斷直線和圓的位置關系呢？

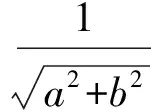
師：前面2位同學都是從形式和表面上得到直線和圓的位置關系的，在實際問題中有的問題具有迷惑性，必須從一般解題方法上加以思考.

評析當學生遇到疑難問題時,引導他們相互交流或師生交流，既能讓常見的理解疑惑或典型錯誤充分暴露，更能通過交流深入尋找形成問題的根源，使學生明確事物的本質特征、相近概念的聯系與區別.在上述片斷中,生12的回答是常見的典型性錯誤，是幫助學生辨析的機會.在這兒,教師抓住機會分別進行了追問，師生的交流讓其暴露了學生思考的過程，然后有針對性地給予了根源上的糾正.

4 不同解法的比較評價中提升思維

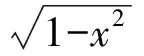
師：你想到解決此問題的途徑了嗎？

生14：用代數方法即解方程組，可知2個不同的交點對應于方程組有2組不同的解.

生15：此方法比較麻煩，需要開根號還要考慮前后的范圍，我通過圓心到直線的距離，可知它們有2個不同交點,即相交.

師：這樣的對應正確嗎？

生16：應該是直線與上半個圓有2個不同的交點.

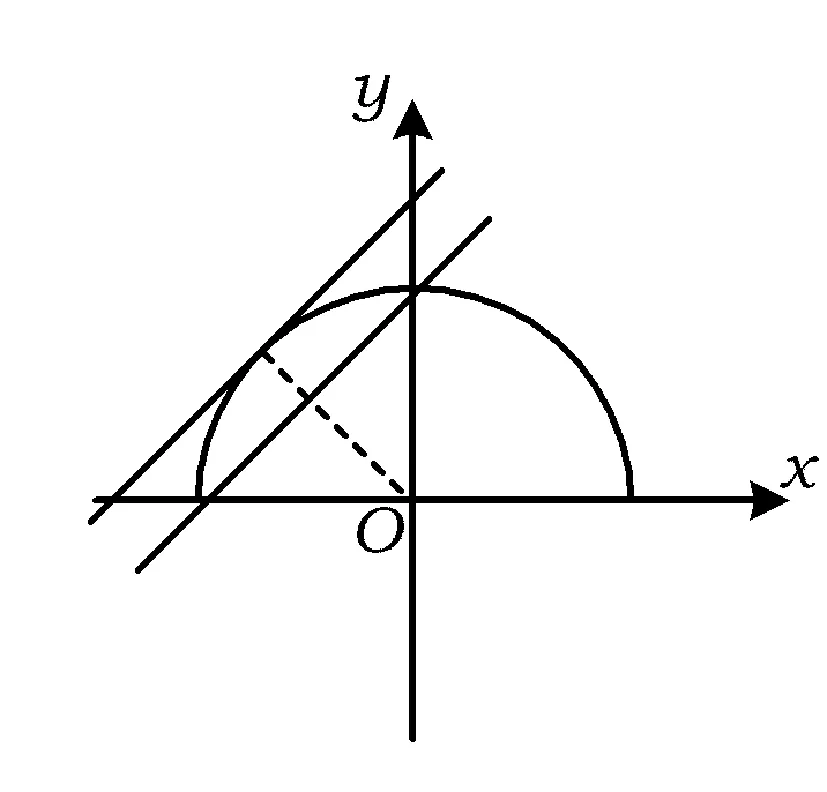
圖1

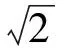
師：比較上述方法，哪種更簡單？

生18：最后的那種方法要簡便些.

師：上述的方法中體現著什么樣的思想？

生18：一是數形結合思想;二是等價轉化思想.

評析數學思想是數學的精髓，學生數學能力的獲得與提高是其自主學習、實現可持續發展的關鍵.教師的課堂評價必須對此有正確的導向，要求教師把握滲透的機會，貫穿于學生數學知識的建構過程與問題的解決過程中.同時需要關注學生能否在理解不同方法的基礎上，針對問題特點進行合理選擇，進而熟練運用.在例4中，教師通過引導學生對不同解法進行評價，在比較中不僅知道了方法的優劣，更是在深入的思想層面上的分析經歷了思維的層次比較.

5 不同問題解決的比較評價中突出實質

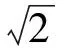
師：是如何解決的？

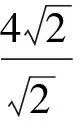
師：還有其他解法嗎？

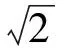
變式1已知圓(x-3)2+(y-3)2=9和直線y=x+b，當b為何值時，圓上恰有3個點到直線的距離等于1(同桌討論).

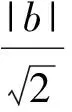
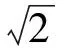
師：上述3個問題的解決中有什么共同點？

生23：它們都是圓上的動點問題，相對比較抽象，解決時都是通過轉化為圓心和半徑的關系求解的.

生24：問題解決過程都是借助圖形直觀，也就是利用數形結合求解.

師：這就是圓上的動點問題轉化為圓心這一定點的一般方法，其中需要形的輔助.

評析對一類數學問題本質的理解,既是有效交流評價的目標，也是課堂交流的途徑和基礎.教師在引導中要從學生的認知出發，設計不同問題或變式問題，引導學生從數學視角、數學模型和數學思想方法等進行問題本質的理解交流.通過例4及其2個變式的解決，然后引導學生對其共同點開展評價，突出了圓上動點問題的一般轉化途徑和蘊含其中的數形結合思想，有利于學生對此類問題的理解掌握.