圓錐曲線中一類問題的推廣及應用

●

(周莊高級中學 江蘇興化 225711)

圓錐曲線中一類問題的推廣及應用

●張乃貴

(周莊高級中學 江蘇興化 225711)

在近幾年的數學高考和競賽中，經常出現與圓錐曲線焦點、焦半徑比、直線斜率有關的一類試題,其典型解法是利用圓錐曲線的第二定義．本文將焦點一般化得到3個用途廣泛的命題，更體現出解析幾何的特點，并且利用3個命題的推論解決圓錐曲線中的這一類問題．

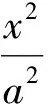
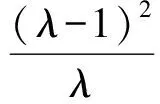
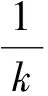
b2(my+t)2+a2y2-a2b2=0，

整理得

(b2m2+a2)y2+2mtb2y+b2(t2-a2)=0.

由韋達定理知

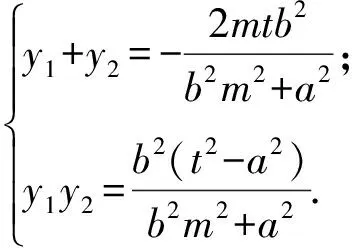
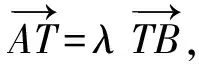
(t-x1,-y1)=λ(x2-t,y2)，

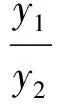
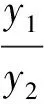
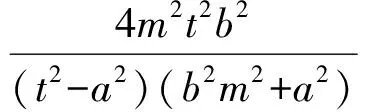
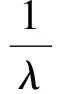
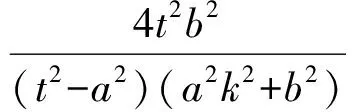
即

( )

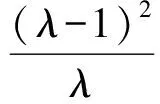
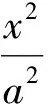
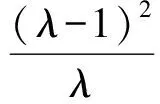
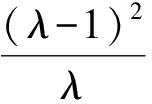
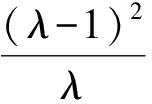
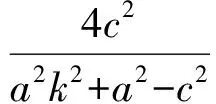
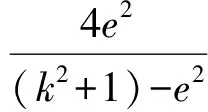
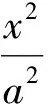
(2010年全國數學高考試題)

解由推論1得

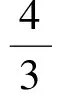
即

k2=4e2-1=2，

解得

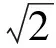
故選B．

( )

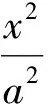
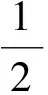
(2010年第21屆“希望杯”全國數學邀請賽試題)

解由推論1得

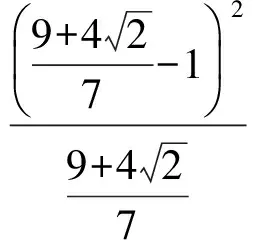
即

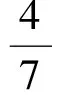
解得

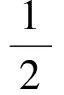
故選A．

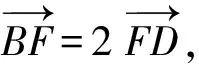
(2010年全國數學高考試題)

解由推論1得

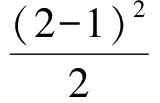
即

9e2=k2+1.

又

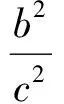
得

從而

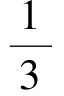
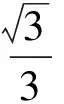
在命題1中,以-b2代換b2,便可得到雙曲線中相應的結論．

( )

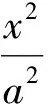
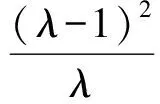
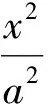
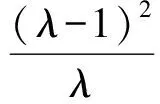
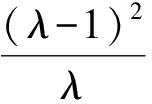
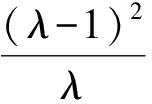
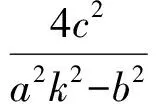
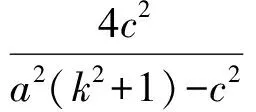
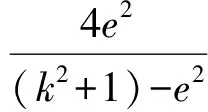
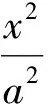
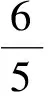
(2009年全國數學高考試題)

解由推論2得

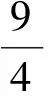
解得

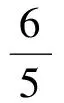
故選A．

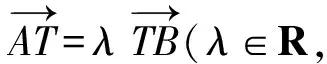
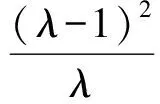
證明設A(x1,y1)，B(x2,y2)，直線方程可設為

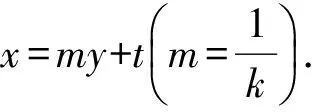
將直線方程與拋物線方程組成方程組

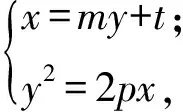
消去x得

y2-2pmy-2pt=0.

由韋達定理得

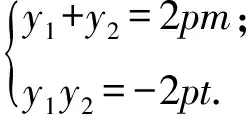
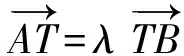
(t-x1,-y1)=λ(x2-t,y2)，

所以

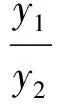
又

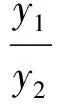
得

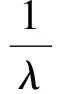
即

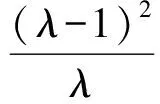
例5已知直線y=k(x+2)(k>0)與拋物線C:y2=8x相交于點A,B，F為C的焦點.若|FA|=2|FB|，則k=

( )

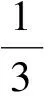
(2009年全國數學高考試題)

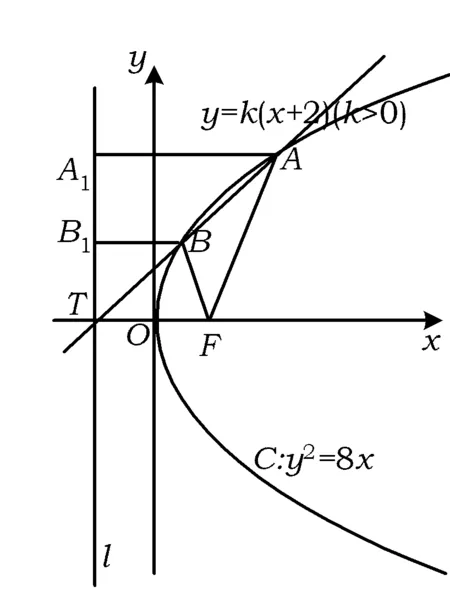
圖1

解如圖1，拋物線C:y2=8x的準線為直線l:x=-2.分別過點A,B作AA1⊥l于點A1,作BB1⊥l于點B1，直線y=k(x+2)(k>0)恒過定點T(-2,0).由拋物線的定義知

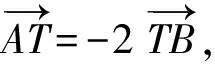
即

λ=-2.

由命題3得

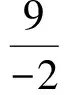
解得

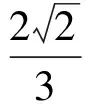
故選D．

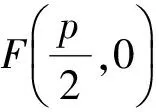
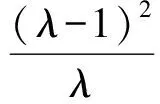
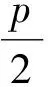
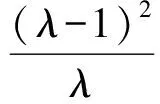
即

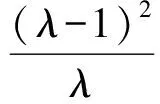
例6已知F是拋物線C:y2=4x的焦點，過點F且斜率為1的直線交C于點A,B．設|FA|>|FB|，則|FA|與|FB|的比值等于________．

(2008年全國數學高考試題)

解由推論3得

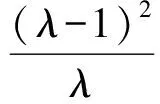
即

λ2-6λ+1=0，

解得

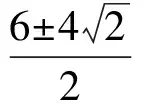
又由|FA|>|FB|，得

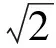
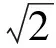
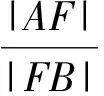
(2008年全國數學高考試題)

解推論3是對焦點在x軸上的拋物線得出的結論，為了能夠使用推論3，將原題等價轉化為：

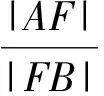
由推論3得

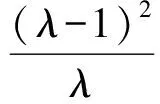
即

3λ2-10λ+3=0,

解得

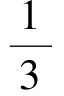
因為點A在x軸下方，所以

|FA|<|FB|，

從而

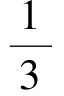
即

推論1，2，3中的結論可以統一為:

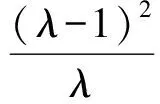
這是數學和諧美的體現．用以上的3個命題可以編制出許多新的數學問題，大家可進行嘗試．