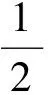解一道數列題的心路歷程

●

(應城市第一高級中學 湖北應城 432400)

解一道數列題的心路歷程

●陶治國高坤

(應城市第一高級中學 湖北應城 432400)

( )

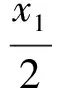
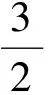
說明這是2011屆湖北省武漢市的二月調研測試題選擇題的第10題.本題主要考查了遞推型的數列問題以及數列的極限，考查學生的邏輯推理能力.

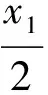
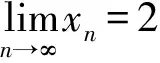
評注排除法是一種不錯的選擇，關鍵在于要理解xn-1與xn-2取中點為xn.

解法2由題意可知

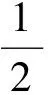
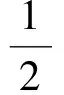
因此

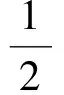
兩邊同時取極限得

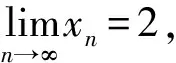
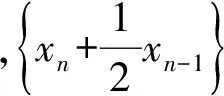
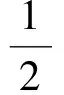
然后利用極限的思想求得.

解法3由題意可知

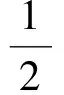
令

xn+1+αxn=β(xn+αxn-1),

由待定系數法可得

解得

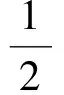
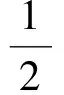
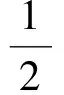
即

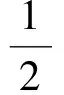
(1)

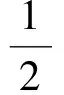
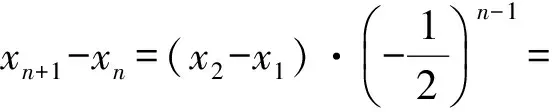
(2)

式(1)-式(2)得

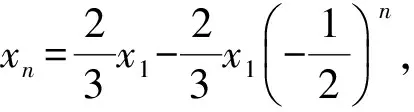
因此

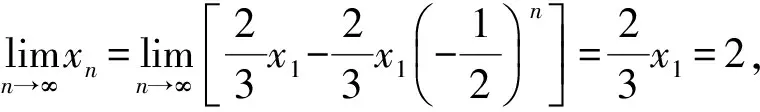
解得

x1=3.

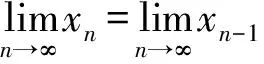
通過解法3可以得到數列關于相鄰3項之間更一般的結論.例如：已知an+1=pan+qan-1,設an+1-tan=s(an-tan-1),則

an+1=(s+t)an-stan-1,

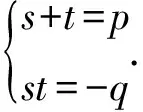
(1)若方程組有2組不同的解(s1,t1),(s2,t2)，則

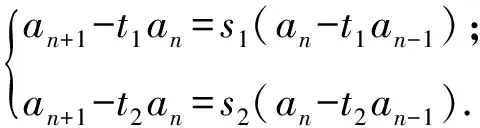
由等比數列性質得

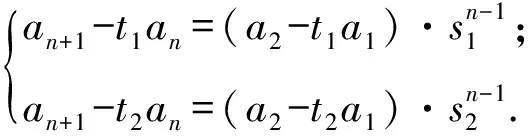
因為t1≠t2，由上兩式消去an+1可得

(2)若方程組有2組相同的解,則

s1=s2,t1=t2,

易證此時s1=t1，從而

an+1-t1an=s1(an-t1an-1)=

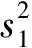
得

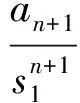
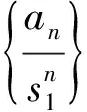
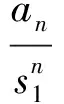
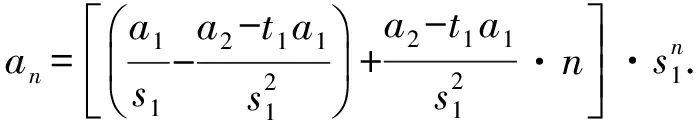
(3)若方程組有一對共軛虛根r(cosθ±isinθ),則不難求得

an=(c1·cosnθ+c2sinnθ)·rn,

證明過程留給讀者.

例1已知a1=a2=1,an+1=an+an-1(n=2,3,…)，求通項公式an.

解由特征根方程x2-x-1=0,得

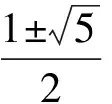
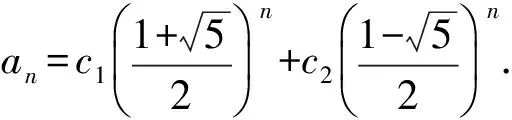
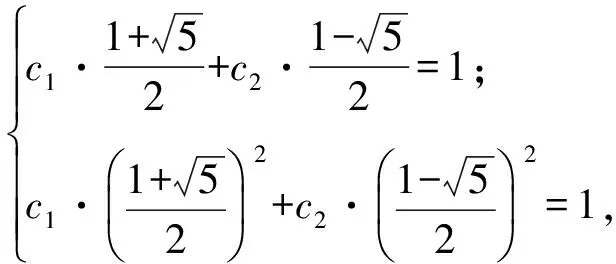
解得

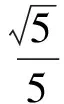
因此

例2已知數列a1=1,a2=5,且an+1=4an-4an-1(n≥2),求an.

解由特征根方程x2-4x+4=0,得

x1=x2=2.

設通項為an=(c1+nc2)·22,由條件知

解得

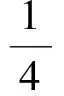
于是

an=(3n-1)·2n-2.

例3已知數列a1=0,a2=1，且an+1=2an-2an-1(n≥2),求通項an.

解特征根方程為

x2-2x+2=0,

得

從而

由初始條件得

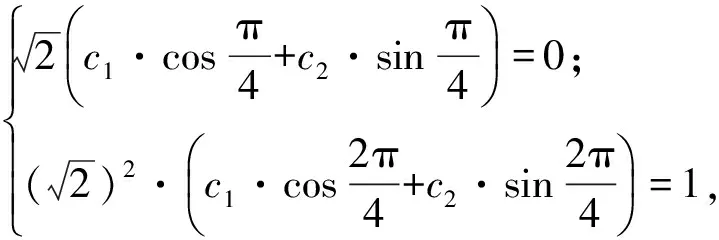
解得