排序學習算法的一般模型研究

陳洪

華中農業大學理學院, 湖北武漢430070

排序學習算法的一般模型研究

陳洪

華中農業大學理學院, 湖北武漢430070

排序學習問題是機器學習與數據挖掘領域近來的研究熱點之一。 本文通過分析和比較幾種排序學習模型，提出基于這些模型的一般框架，從而為進一步的算法設計和理論分析奠定基礎。

排序; 機器學習; 模型選擇

隨著排序機器學習算法在信息抽取，信用評價，產品推薦以及病理分析等領域的廣泛應用，排序學習算法的設計和理論分析成為機器學習研究的熱點課題之一。本文著重研究排序算法設計中的優化目標函數的選擇問題。

一、排序學習的一般前提[3]

給定訓練數據集合A，我們采用有向關系圖G=(V,E)來表示數據間的序關系。同時用表示假設函數集合。詳細來說，關系如下：

1.訓練數據

這里描述的排序背景適合于分析和處理許多不同類型的經典排序模型。

二、幾種排序模型

本節介紹幾種常見的排序學習的目標函數，基于這些目標函數設計的排序學習算法在經驗數據實驗中顯示了良好的性能。

1.二劃分排序[1]

二劃分排序問題是一種經典的排序問題，這里類別數只有兩類。學習的目的就是使兩類數據能順利的區分開來。其對應的優化目標函數為

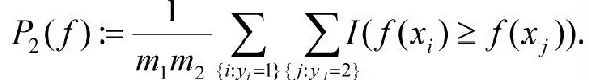
2.K-劃分排序（詳見[2]）

在K-劃分排序排序問題中，給定的樣本往往具有K個序標。因此，對應的優化目標函數為二排序優化目標函數的推廣，其表達式如下

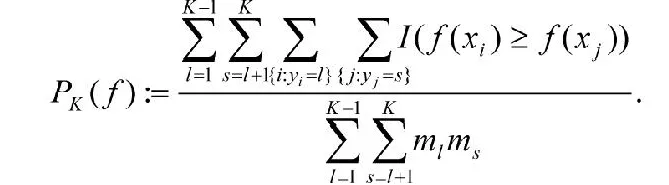
雖然基于此目標的推廣誤差的界已經在[2]中建立，但是該目標僅適合處理全相關的排序情形，在實際應用中受到很多限制。

3.推廣的Wilcoxon-Mann-Whitney（WMW）統計

WMW統計原用于獲得分類學習問題大偏差的界，近來被引入排序學習問題中。推廣的WMW定義如下

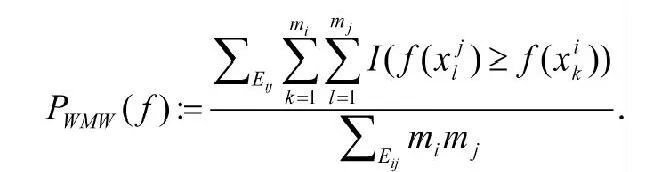
基于此目標，一類快速的梯度下降算法在[3]中被提出，并且在數據實驗中顯示了良好的性能。然而，在實際排序問題中，往往更關注頂端的排序準確性，因而推廣該目標到關注頂端排序問題是很有意義的一個課題。

4.p模排序

在文獻[4]中，作者提出了一種新的優化目標函數，其優點在于能有效的強調排序問題頂端的排序性能。對應的目標函數定義為：

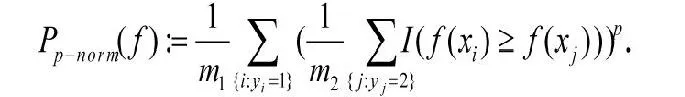
顯然p模排序是基于二排序問題，其應用范圍因此也受到較大限制。

三、排序學習的一般模型

基于以上幾種排序優化函數，提出如下排序學習算法的一般模型：

該目標函數不僅能通過調整 p值的大小來強調頂端排序的準確性，也適合于處理各種排序關系問題，從而有更廣泛的前景。

同時，從算法的理論分析來看，通過該模型的研究，有助于建立排序學習算法推廣性能分析的統一理論基礎，為進一步模型選擇，算法設計以及參數選擇提供理論指導。

該目標函數與前面幾種目標函數的關系總結如下表：

?

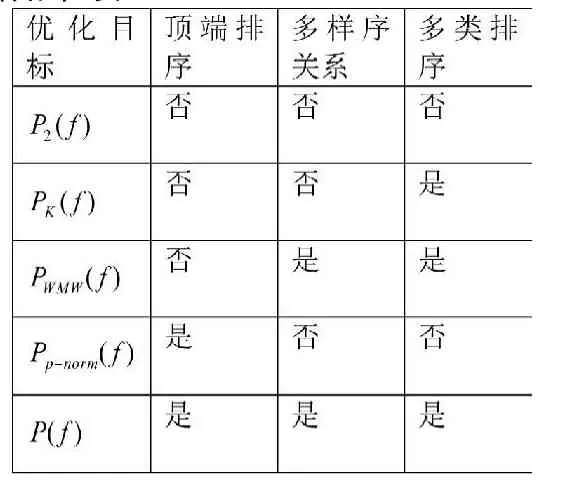
四、小結

排序學習的理論和應用研究是近來機器學習和數據挖掘研究的熱點問題之一。如何設計合理的算法模型是排序問題的關鍵。本文結合已有的模型，給出了一般條件下的優化目標模型。該模型適用更廣泛的應用領域，且有助于建立排序學習算法統一的理論基礎。

[1]S.Agarwal, et.al.Generalization bounds for the area under the ROC curve[J].JMLR,2005,6:393-425

[2]S.Rajaram,S.Agarwal．Generalization bounds for k-partite ranking[J].In NIPS, 2005

[3]V.C.Raykar, et.al.A fast algorithm for learning a ranking function from large-scale data sets[J].TPAMI, 2009, 30：1158--1170

[4]C.Rudin.The p-norm push: a simple convex ranking algorithm that concentates at the top of the list[J].JMLR, 2009,10：2233--2271

TP181

A

10.3969/j.issn.1001-8972.2011.13.081