精確行波解的構造及其應用＊

馮濱魯

（濰坊學院，山東 濰坊 261061）

精確行波解的構造及其應用＊

馮濱魯

（濰坊學院，山東 濰坊 261061）

通過利用修正里卡蒂方程得到一個構造精確行波解的方法，并且舉出例子來展現這一方法在處理非線性波方程上的應用。

構造；行波解；Kdv方程

1 引言

非線性物理現象同非線性偏微分方程（NLPDEs）緊密相聯，并且涉及到許多其他領域，如生物、化學、力學等等。作為這些現象的數學模型，NLPDEs的精確解的研究將幫助我們更好地理解這些現象，所以許多學者研究找到了多種方法來求精確解，如反散射方法［5－6］、hirota雙線性方法［7－9］、tanh方法［10－12］、齊次平衡法等。本文通過利用修正里卡蒂方程獲得一個構造精確行波解的新方法，并且舉出例子來展現這一方法在處理非線性波方程上的有效應用。

2 主要結果

對于非線性方程

其中，P是一個關于u和u的各階偏導數的一個多項式，為得到方程（1）的行波解，作如下變換

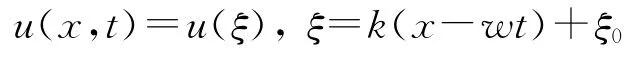
這里，k，w為待定常數，ξ0為任意常數。

那么方程（1）就變成一個常微分方程

假設方程有如下形式的解

由文獻［1］知Y滿足下面的方程

其中，m和r是整數，ci（i＝1，2，…，r）是待定常數，m和r的關系可通過平衡最高階導數項和非線性項得到。如果m不是一個整數，則可通過相應的變換公式［1］來解決。然后將方程（3）代入常微分方程（2）并使用方程（4）得到一個關于Y的各次冪的一個代數方程，因為Y的各次冪系數都為零，從而得到一個關于k，c，a0，…，an，b1…bn的方程組。利用Mathematica或者Maple就可將它們解出來，最后只需將上面的結果代入到方程（3）便得到方程（1）的解。……