廣義非線性互補問題的非光滑牛頓算法＊

李梅霞，田治平

（濰坊學院，山東 濰坊 261061；山東科技職業學院，山東 濰坊 261053）

廣義非線性互補問題的非光滑牛頓算法＊

李梅霞，田治平

（濰坊學院，山東 濰坊 261061；山東科技職業學院，山東 濰坊 261053）

研究了一類在多項式錐上的廣義非線性互補問題。借助罰FB互補函數建立了該類問題的非光滑方程，提出了求解該方程的非光滑牛頓算法，證明了與互補函數有關的穩定點即為廣義非線性互補問題的解。在較弱的條件下給出了牛頓算法的全局和超線性收斂性。

廣義非線性互補問題；罰FB互補函數；穩定點；超線性收斂

1 引言

考慮廣義非線性互補問題（簡記為GNCP（F，G，κ））：尋求向量x＊∈Rn使得

其中F，G：Rn→Rm，κ?Rm為非空閉凸錐，κ0為κ的極錐。

廣義非線性互補問題在工程和經濟中具有廣泛的應用。近幾年來，其理論和算法都得到了較快發展〔1〕。特別地，當κ＝且G（x）＝x時，廣義非線性互補問題即為傳統的非線性互補問題［2］。

在本文中，我們將考慮一類特殊的廣義非線性互補問題，即m＝n，F和G均為Rn上的連續可微函數，κ為Rn上的多項式錐，即存在A∈Rs×n使得

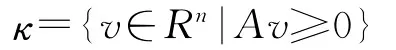
易證κ的極錐為

對于A＝I的情況，文獻［3］中應用一類互補函數研究了該類問題的解與無約束極小化問題的最優解之間的關系。而對于κ＝｛v∈Rn｜Av≥0，Bv＝0｝的情況，文獻［4］中應用FB互補函數進行了研究，證明了與互補函數有關的穩定點即為廣義互補問題的解。同時給出了求解對應非光滑方程的非光滑L－M方法，證明了算法的全局收斂性和超線性收斂速度。在本文中，我們將應用罰FB函數［5］研究GNCP（F，G，κ）。眾所周知，罰FB函數具有許多優良性質，借助該類函數我們建立了GNCP（F，G，κ）的非光滑方程，給出了求解該類方程的非光滑牛頓算法，在算法中我們應用了非單調線搜索，這些都使得算法具有較好的收斂性和較快的收斂速度。……