一類超線性離散薛定諤系統的基態解*
周陽鋒, 沈自飛
(浙江師范大學數理與信息工程學院,浙江金華 321004)
0 引言
本文研究離散薛定諤系統

基態解的存在性,即使得系統(1)相應的能量泛函取得最小值的解.式(1)中:-Δun=un+1+un-1-2un是一維空間的離散拉普拉斯算子;給定的序列{εn}關于n是k-周期的.研究系統(1)的動機來自于下面的向量值非線性薛定諤方程:

從而對向量值非線性薛定諤方程的研究轉換成對方程

的研究,這是一個哈密爾頓型的離散薛定諤系統.考慮

的情形,其中
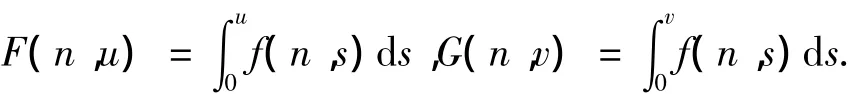
對離散薛定諤系統的研究引起了不少數學家的興趣,因為它為很多物理問題提供了一個很好的數學模型[1-2].文獻[3]得到了系統(1)在Ambrosetti-Rabinowitz條件下有無窮多解的結論.
本文主要考慮不含Ambrosetti-Rabinowitz條件時離散系統(1)基態解的存在性問題.假設εn,f,g滿足如下條件:
(V0)εn關于n是k-周期的,且0在-Δ+εn的譜間隙中;
(H1)f(n,s),g(n,s)關于 s∈R 連續,關于 n 是 k-周期的;
(H2)存在 C >0,p,q∈(2,+∞),使得|f(n,s)|≤C(1+|s|p-1),|g(n,s)|≤C(1+|s|q-1);
(H3)當|s|趨于 0 時,關于 n 一致有 f(n,s)=o(|s|),g(n,s)=o(|s|);

本文的主要結果是:
定理1 在(V0)和(H1)~(H5)條件下,系統(1)至少有1個基態解.
1 變分框架
在希爾伯特空間E=l2×l2上考慮泛函

式(3)中:(·,·)是普通的 l2內積;A=-Δ + εn;z={zn}={un,vn}∈l2×l2.
為了方便,記l2:=l2×l2,相應地記ls:=ls×ls,s∈(2,+∞).E 中范數記作‖·‖,顯然 Φ(z)是一個在E中定義良好的C1-泛函,系統(1)可以看成泛函Φ相應的Euler-Lagrange方程.
引理 1[3]若{εn}關于 n 是 k-周期的,即 εn+k= εn,則
1)A是有界自伴算子;
2)σ(A)=σe(A)?R(-a,a);
3)σ(A)關于0對稱,即σ(A)∩(-∞,0)=-σ(A)∩(0,+∞).
由引理1可知E有如下的正交分解:

其中,E+(E-)是A在E中正(負)譜空間.從而(Az,z)=‖z+‖2-‖z-‖2,泛函(3)可寫成
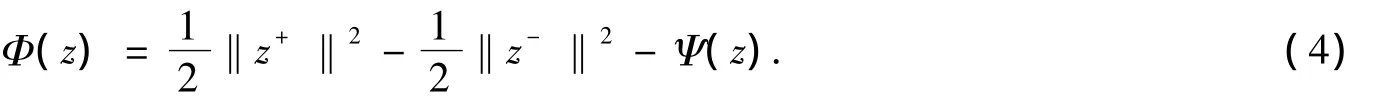
式(4)中
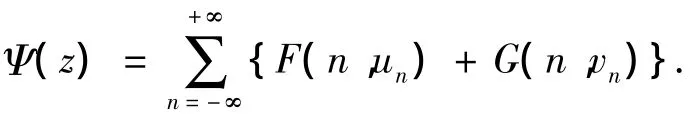
設希爾伯特空間E有正交分解E=N+⊕N-,其中N?E是E的一個閉的可分子空間.設z=v+w∈E=N⊕N⊥,滿足 v∈N,w∈N⊥.定義|z|2w=|v|2w+‖w‖2.特別地,若 zn=vn+wn有界,zn在|·|w中弱收斂到z,則vn在N中弱收斂到v,wn在E中強收斂到w.記Br(E)={z∈E|‖z‖≤r},Sr(E)={z∈E|‖z‖ =r};令 E=E+⊕E-,z0∈E+滿足‖z0‖ =1,N=Br(E+)⊕E-;設 M:={z=sz0+z-| ‖z‖≤r,s>0}滿足 s0z0∈M,s0>0;令 Q:={z=sz0+z+|z+∈N⊥,‖z0‖ =s0,s >0};Γ:={h|h:[0,1]×M→E}是|·|w-連續的,h(0,z)=z,Φ(h(s,z))≤Φ(z),?z∈M.任意(s0,z0)∈[0,1]×M,存在|·|w-鄰域U(s0,z0),使得{z-h(t,z)|(t,z)∈U(s0,z0)∩([0,1]× M)?Efin}.其中,Efin是指 E 的有限維子空間.文獻[4]給出的定理在本文的證明中起著重要作用.
引理2[4]記 Φλ(z):=I(z)-λJ(z)∈C1,z∈E,?λ∈[1,2],假設:
1)J(z)≥0;
2)若‖z‖→∞,則I(z)→∞或J(z)→∞;
3)Φλ是|·|w-上半連續的,Φ'λ在E上是弱序列連續的,且Φλ將有界集映為有界集;

則對幾乎所有 λ∈[1,2],存在{zn},使得

其中

2 定理1的證明
考慮

理2 中的條件1)和2)成立.若關于|·|w范數 zm→z,Φλ(zm)≥a,則 z+m→z+,z-m?z-,從而 zm,n→zn對幾乎所有n∈Z成立.由Fatou引理得Φλ(z)≥a,這意味著Φλ是|·|w-上半連續的.由文獻[4]得Φ'λ在E上弱序列連續且Φλ將有界集映為有界集.為了應用引理2,只需驗證引理2中的條件4)成立即可.
引理3 在條件(V0)和(H1)~(H5)下,有如下結論成立:
1)存在 ρ>0,使得 κ:=inf Φλ(S■(E+))>0;
2)對任意給定的 z0∈B1(E+),存在 R > ρ> 0,使得 sup Φλ(?M)≤0.
證明 1)不失一般性,不妨假設p<q.由(H2)知,對任意ε>0,存在Cε>0,使得

從而對任意z∈E+,有

這就導出了矛盾,從而1)成立.

由F(n,s)>0,G(n,s)>0和 Fatou引理得
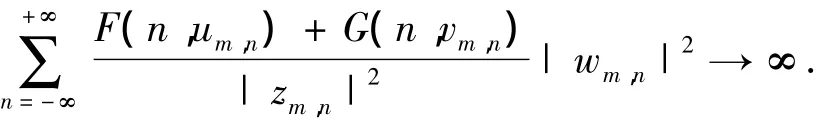
這與式(6)矛盾.從而假設不成立.引理3證畢.
應用引理2,可得到如下引理:
引理4 在條件(V0)和(H1)~(H5)下,對幾乎所有λ∈[1,2],存在序列{zm}?E,使得

引理5 設條件(V0)和(H1)~(H5)成立,{zm}是(PS)-序列,則下列2個結論中必有1個成立:
1)‖zm‖→0;
2)存在 δ>0,am∈Z,使得|zm,am|≥δ對 m∈Z 都成立.
證明 由引理4知{zm}在E上有界.假設2)不成立,則對任意 η >0,n∈Z,|zm,n|<η.由H?lder不等式得

由ε的任意性得
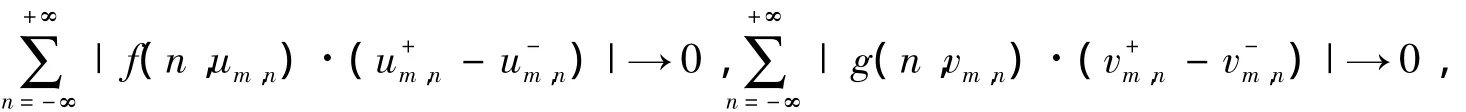
從而

因此1)成立.引理5證畢.
引理6 在條件(V0)和(H1)~(H5)下,對幾乎所有 λ∈[1,2],存在 zλ,使得

證明 因為{zm}有界,所以{z+m}有界.由引理5知如下兩者必有1個成立:

2)存在δ>0和am∈Z,使得|z+m,am|≥δ對任意m ∈Z成立.
如果‖z+m‖→0,那么對任意 s∈(2,+∞),在 ls中有 z+m→0.因為對任意 ε >0,存在 Cε>0,使得|f(n,s)|≤ε|s|+Cε|s|p-1,|g(n,s)|≤ε|s|+Cε|s|p-1,所以由 H?lder不等式得

從而

這意味著zλ是個弱解.由(H5)得

應用Fatou引理,得到

引理6證畢.
引理7 設 u,v,s∈R,s≥ -1 且 w:=su+v≠0,則對 n∈Z,有
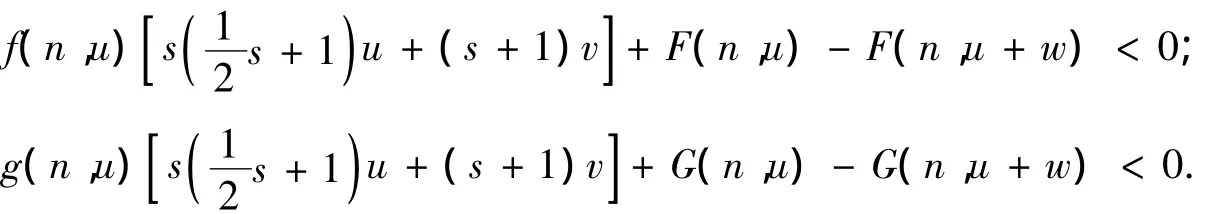
證明 類似于文獻[5],故略.
引理8 設zλ是由引理6得到的臨界點,則對任意w∈Σ:={szλ+ζ|s≥ -1,ζ=(u,v)∈E-},w≠0,有 Φλ(zλ+w)< Φλ(zλ).
證明 把Φλ寫成如下形式:

因為(Φ'
λ(zλ),ζ)=0,所以

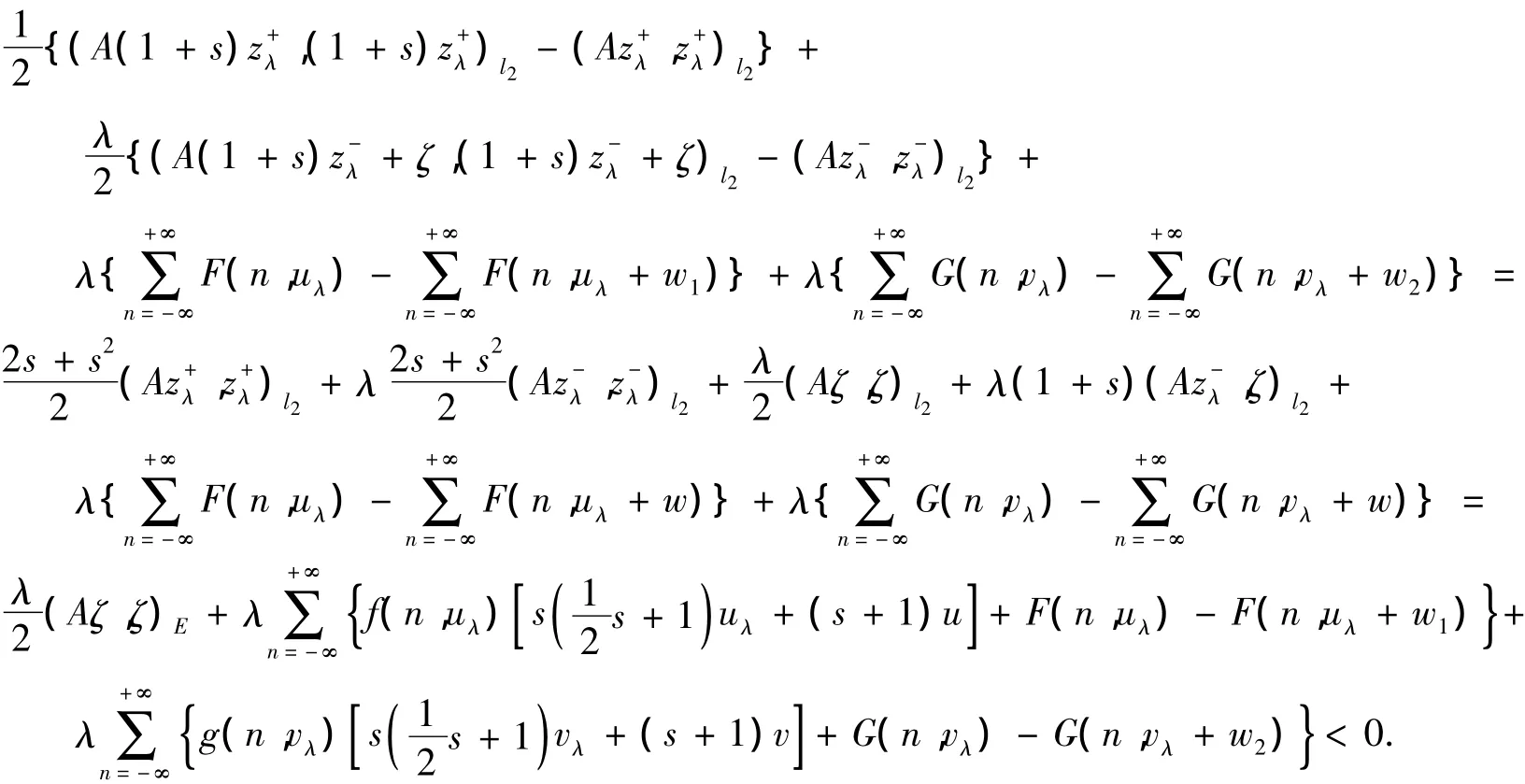
引理8證畢.
引理9 在條件(V0)和(H1)~(H5)下,存在λm→1和序列{zλm},使得

當r足夠大時,可由此式導出矛盾,從而{am}可以選取為有界序列.由Fatou引理得到

從而當m→+∞時,
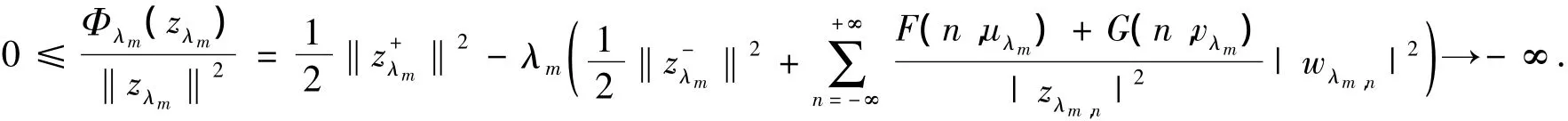
這就導出了矛盾,從而可得引理9成立.
引理10 在條件(V0)和(H1)~(H5)下,對 λm→1和序列{zλm},有

證明 對于 ζ滿足‖ζ‖≤1,因為{zλm}有界,所以

從而可得引理10成立.
定理1的證明 因為{zλm}有界,所以下面兩者必有1個成立:
1)‖zλm‖→0;

類似可得

所以Φ(z)=C>0,即z是系統(1)的基態解.定理1證畢.
[1]Ablowitz M,Prinari B,Trubatch A.Discrete and continuous nonlinear Schr?dinger system[M].Cambridge:Cambridge University Press,2004:1-5.
[2]Bruno G,Pankov A,Tverdokhleb Y.On almost-periodic operators in the spaces of sequences[J].Acta Appl Math,2001,65(3):153-167.
[3]Yang Minbo,Zhao Fukun,Ding Yanheng.Infinitely many stationary solutions of discrete vector nonlinear Schr?dinger equation with symmetry[J].Nonl Anal,2010,215(12):4230-4238.
[4]Schechter M,Zou W.Weak linking theorems and Schr?dinger equations with critical Sobolev exponent[J].ESAIM Control Optim Calc Var,2003,37(9):601-619.
[5]Szulkin A,Weth T.Ground state solutions for some indefinite problems[J].J Funct Anal,2009,257(12):3802-3822.

