范德瓦爾斯氣體的卡諾循環(huán)效率

藍風華

(武警工程學院物理教研室,陜西西安 710086)

范德瓦爾斯氣體的卡諾循環(huán)效率

藍風華

(武警工程學院物理教研室,陜西西安 710086)

以范德瓦爾斯氣體為工作物質推導出的卡諾循環(huán)效率,只與熱源的溫度有關,與工作物質是否是理想氣體無關.

范德瓦爾斯氣體;卡諾循環(huán)效率

在大學物理教科書中,我們知道理想氣體卡諾循環(huán)效率為

η與理想氣體的工作物質無關,只與高溫熱源的溫度 T1及低溫熱源的溫度 T2有關.對于卡諾循環(huán)的研究不僅為提高熱機效率指明了方向和限度,而且對熱力學第二定律的建立起了重要的作用.

實際上,熱機的工作物質一般都不是理想氣體,那么實際氣體的卡諾循環(huán)效率應滿足什么關系,對于非理想氣體是否仍遵守式 (1).范德瓦爾斯在研究實際氣體時,考慮到氣體分子的體積和分子間的引力,對理想氣體狀態(tài)方程進行了修正,從而得到實際氣體的范德瓦爾斯方程,即νmol氣體的狀態(tài)方程為

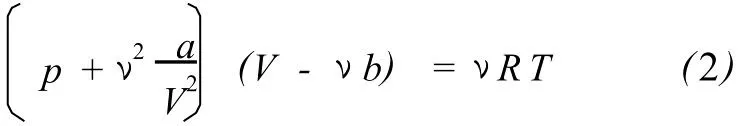
其中,a,b為范德瓦爾斯常量,可由實驗測得.把完全遵守式 (2)的氣體稱為范德瓦爾斯氣體,它比理想氣體更接近實際氣體.下面就以范德瓦爾斯氣體為工作物質來研究卡諾循環(huán)效率.

1 絕熱過程方程

當范德瓦爾斯氣體經歷一個準靜態(tài)絕熱過程時,系統與外界無熱交換,即 dQ=0,系統的內能變化為[1]

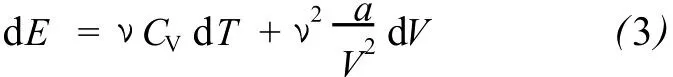
其中,CV為氣體定體摩爾熱容.

系統對外做功

根據熱力學第一定律

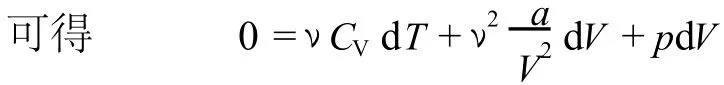
再結合式 (2),就有

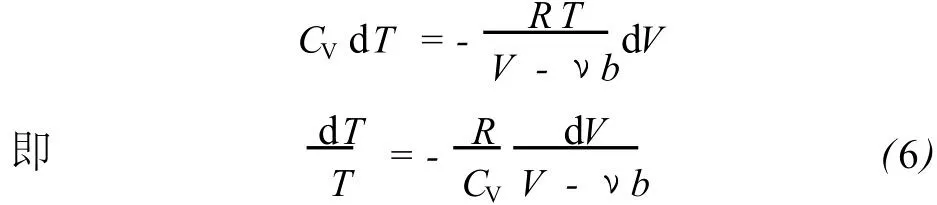
對式 (6)積分,并整理可得

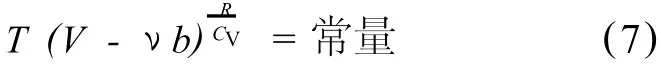
這就是范德瓦爾斯氣體絕熱過程的過程方程.

由式 (7)和式 (2)還可以得到用 p、V表示的絕熱過程方程,即

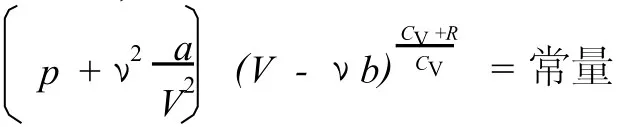
2 等溫過程吸收的熱量

當范德瓦爾斯氣體作準靜態(tài)的等溫變化時,系統吸收的熱量,由式 (3)、(4)、(5)聯立可得

考慮到等溫過程 dT=0,再結合式 (2)就有

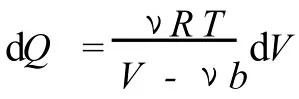
對于有限過程,體積由 V1變化到 V2,系統吸收的熱量為

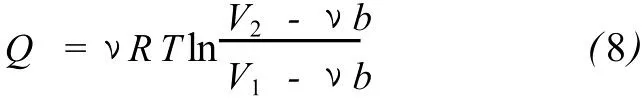
3 卡諾循環(huán)效率

卡諾熱機的循環(huán)過程為卡諾循環(huán),它是由兩個等溫過程和兩個絕熱過程構成的循環(huán).

下面討論以范德瓦爾斯氣體為工作物質的卡諾循環(huán).如圖1所示,在 1→2等溫膨脹過程中,體積由 V1增大到 V2,氣體從高溫熱源 (溫度為 T1)吸收的熱量由式 (8)可得

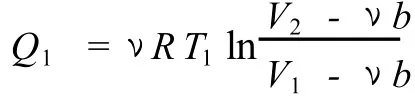
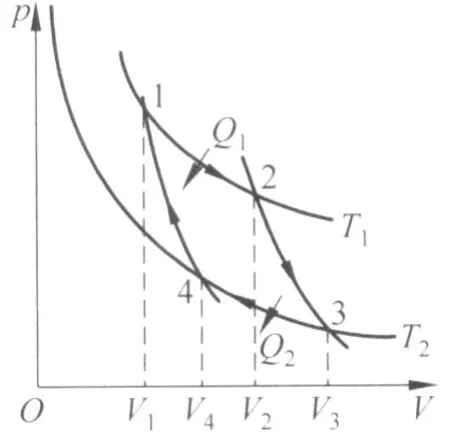
圖1 卡諾循環(huán)

同理,在 3→4等溫壓縮過程中,體積由 V3壓縮到 V4,氣體向低溫熱源(溫度為 T2)放出的熱量為

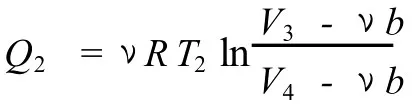
由循環(huán)效率的定義,可得卡諾循環(huán)效率為

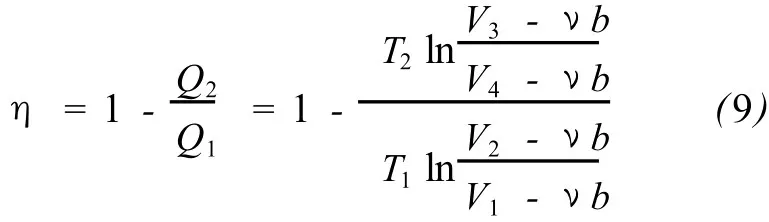
對于 2→3和 4→1兩絕熱過程,根據式 (7)有如下關系

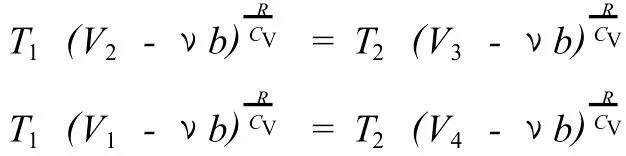
兩式相比可得

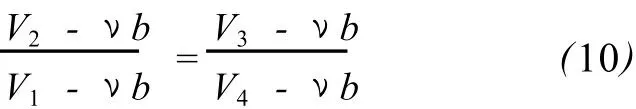
將式 (10)代入式 (9),于是范德瓦爾斯氣體的卡諾循環(huán)效率可表示為

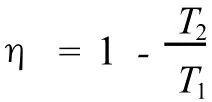
它與理想氣體卡諾循環(huán)效率表達式完全一致.這就是說,卡諾循環(huán)的效率,只與熱源的溫度有關,與工作物質是否是理想氣體無關.

[1] 張三慧.大學物理學:熱學 [M].北京:清華大學出版社,1999.141～142

CARNOT CYCLE EFFI CIENCY OF VAN DERWAALS GAS

Lan Fenghua
(Engineering College of Armed Police and Engineering,Xi’an,Shanxi 710086)

Taking the Van der Waals gas as the working material,we deduced the Carnot cycle efficiency,which is only related to temperature of the heat source and independent of whether the working material is ideal gas.

Van derWaals gas;Carnot cycle efficiency

2010-10-02)