可限制李三系
董艷芹,佟守愚,華宏圖
(1.空軍航空大學基礎部,吉林長春 130022;2.東北師范大學數(shù)學與統(tǒng)計學院,吉林長春 130024)
可限制李三系
董艷芹1,2,佟守愚1,華宏圖1
(1.空軍航空大學基礎部,吉林長春 130022;2.東北師范大學數(shù)學與統(tǒng)計學院,吉林長春 130024)
給出了可限制李三系的定義,討論了限制李三系和可限制李三系的等價關系,并通過可限制李三系,討論了限制李三系的存在性問題.
李三系;限制李三系;可限制李三系
1 預備知識
李三系源于微分幾何中黎曼對稱空間、全測地流形、Jordan代數(shù)和李代數(shù)的研究.限制李三系(特征p域上的李三系)作為一個新興的研究領域,它的發(fā)展還處在起步階段.2001年,T.L.Hodge給出限制李三系的定義,并討論了限制李三系和它的包絡代數(shù)之間的關系[1].2002年,T.L.Hodge又討論了限制李三系的表示論[2].本文主要運用李三系和模李代數(shù)的知識和手法來研究可限制李三系[3-7].在本文中,除了另外表明,k都是特征p域,其中p是大于2的素數(shù).
定義1.1若T是一個關于三元積封閉的向量空間,并且對任意a,b,c,d,e∈T,滿足下面等式:
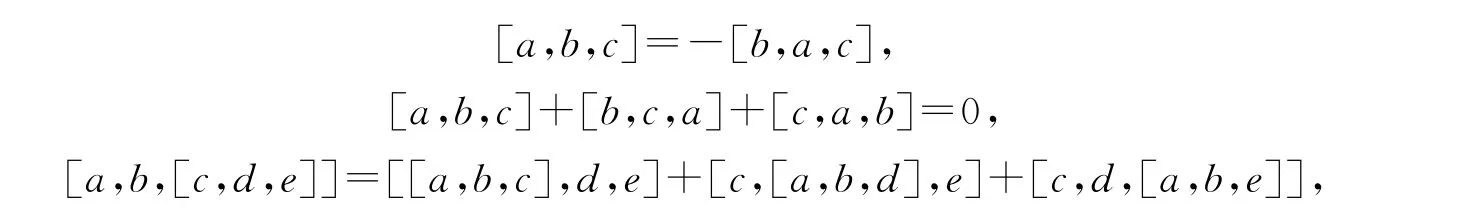
則稱T為李三系.
定義1.2T是一個李三系,任意x,y,z∈T,我們定義L(x,y)∈EndT,使得L(x,y)z=[x,y,z],并且L(T,T)表示由{L(x,y)|x,y∈T}線性張成的空間.定義T的標準嵌入李代數(shù)Ls(T)=L(T,T)⊕T,它的運算為
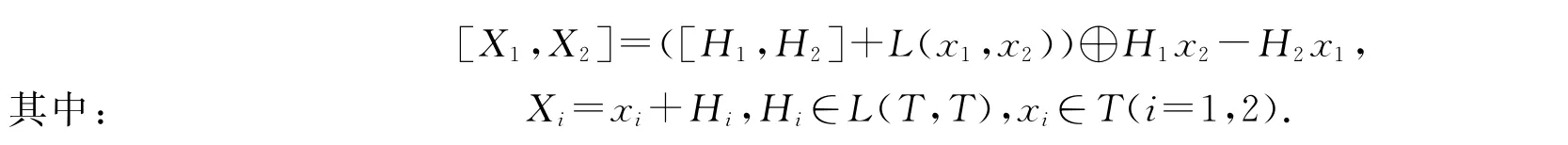
定義1.3李三系T的中心Z(T)定義為Z(T)={x∈T|[x,a,b]=0,?a,b∈T}.
定義1.4若李三系T滿足[x,y,z]=0,?x,y,z∈T,則稱T為交換李三系.
定義1.5李三系T到的一個線性映射Φ:T→,若滿足
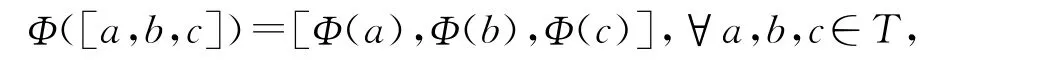
則稱Φ為李三系T到的同態(tài).
定義1.6李三系T的子空間φ,如果滿足[φ,φ,φ]?φ,則稱φ為李三系T的子系.
定義1.7李三系T的子空間φ,如果滿足[φ,T,T]?φ,則稱φ為李三系T的理想,表示為φ?T.定義1.8設φ是李三系T的理想,定義φ0∶=φ.當n≥0,定義φn+1∶=[φn,T,φ]+[φ,T,φn].
定義1.9[2]設T是任意一個李三系,T的標準嵌入李代數(shù)是Ls(T)=L(T,T)⊕T,對于任意N≥3的正奇數(shù),任意x1,x2,…,x N∈T,我們定義:

定義1.10[2]設T是域k上的一個李三系.如果存在一個映射[p]:T→T,并且對任意a,b,c∈T,α∈k,滿足下面等式:
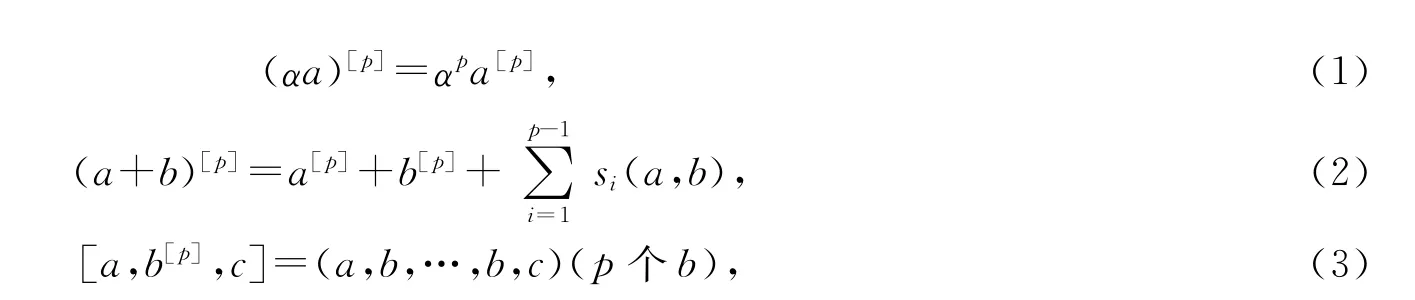
其中isi(a,b)是λi-1在(ad(λa+b))p-1(a)中的系數(shù)(由文獻[1]的命題3.9知si(a,b)∈T),則稱T為限制李三系.
引理1.1[2]T是k上的李三系,如果存在T的基{ui}i∈I,使得對每個i∈I與任意a,c∈T,都存在vi∈T,滿足
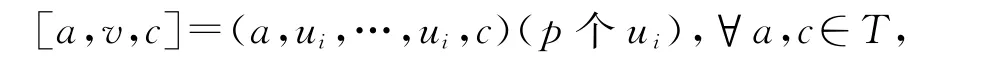
那么T上存在唯一的限制結構a|→a[p],?a∈T,滿足u[p]i=vi,?i∈I.
2 可限制李三系
定義2.1T是k上的李三系,若任意a,b,x∈T,都存在一個y∈T,使得
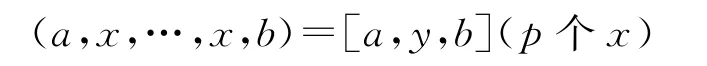
成立,則稱T是可限制李三系.
下面是可限制李三系的兩個例子.
例1每個域k上的交換李三系是可限制李三系.
例2T是k上李三系,若Ls(t)是可限制李代數(shù),那么T是可限制李三系.
事實上,因為Ls(T)是可限制李代數(shù),任意x∈T,都存在y∈Ls(T),使得(adx)p=ady.若y∈L(T,T),上面等式兩邊同時作用T中元素a,有
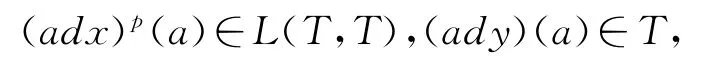
這就導致矛盾,因此y∈T,并且有
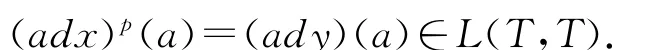
兩邊再同時作用T中元素b,則有
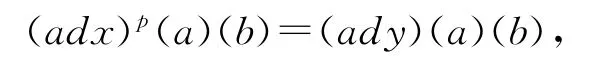
即
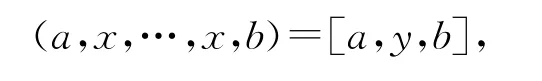
因此T是可限制李三系.
定理2.1T是可限制李三系當且僅當T是限制李三系.
證明充分性.若T是可限制李三系,那么根據(jù)定義2.1,對任意x∈T,都存在y∈T,使得
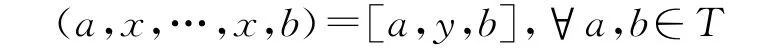
成立.特別的,對T中的一組基{ui}i∈I,一定存在vi∈T,滿足
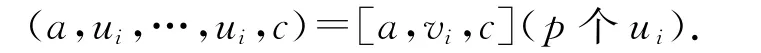
因此根據(jù)引理1.1,T是限制李三系.
必要性.若T是限制李三系,根據(jù)定義1.10中的等式(3),對任意x∈T,都存在x[p]∈T,使得下式成立:
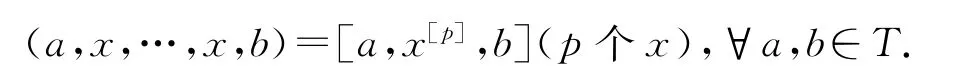
因此根據(jù)定義2.1,T是可限制李三系.
注意在很多時候用可限制李三系比限制李三系更為方便.
定理2.2設f是李三系T1到李三系T2的滿同態(tài).若T1是可限制李三系,則T2也是可限制李三系.
證明由于f是T1到T2的滿同態(tài),對任意a2,x2,b2∈T2,都存在a1,x1,b1∈T1,使得a2=f(a1),x2=f(x1),b2=f(b1).因而
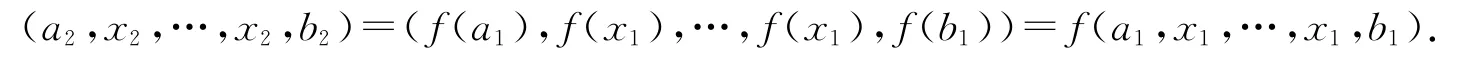
又由于T1是可限制李三系,所以對任意x1∈T1,都存在y1∈T1,使得
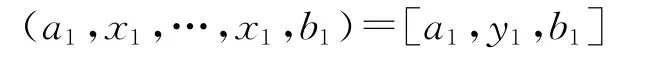
成立.因此,我們有
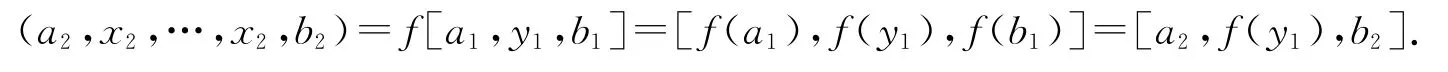
即T2是可限制李三系.
引理2.1T1,T2是李三系,在T=T1⊕T2這個向量空間上,我們定義:
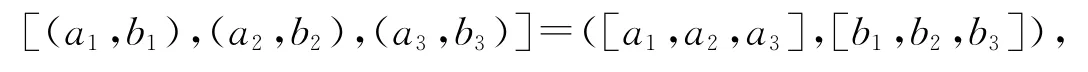
那么T=T1⊕T2是一個李三系,并且T1,T2是T=T1⊕T2的理想.
根據(jù)李三系的定義容易驗證此結論.
定義2.2T是k上的李三系,I是T的理想,若任意x∈I,都存在y∈I,使得(a,x,…,x,b)=[a,y,b](p個x),?a,b∈I成立,則稱I為可限制理想.
定理2.3T1,T2是k上李三系T的理想,并且滿足T=T1⊕T2,那么T是可限制的李三系當且僅當T1,T2是可限制的理想.
證明充分性.因為T1,T2是T的理想,那么一定存在兩個滿同態(tài)
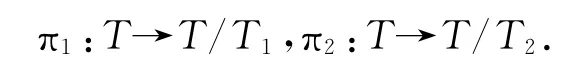
由定理2.2,T/T1,T/T2是可限制李三系,又由于T=T1⊕T2,可知
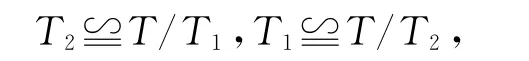
因此T1,T2都是可限制的理想.
必要性.由于T1,T2是可限制的理想,所以對任意x1∈T1,x2∈T2,都存在y1∈T1,y2∈T2,滿足
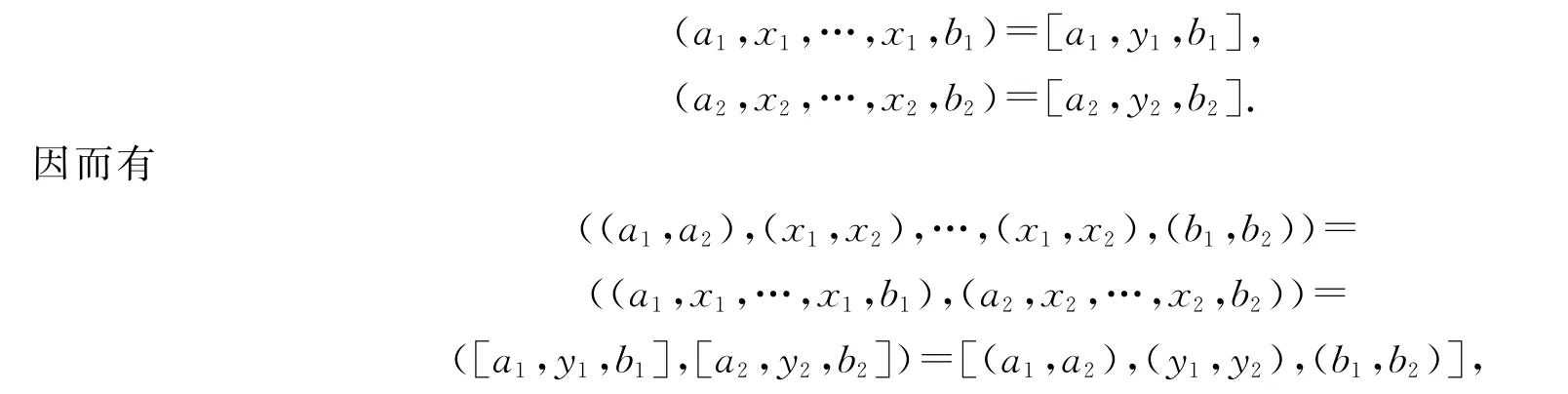
因此T是可限制的李三系.
定理2.4T1,T2是李三系T的可限制理想,且有
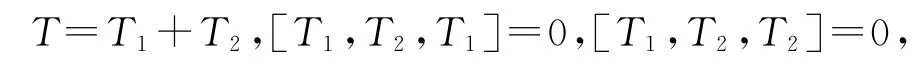
那么T是可限制李三系.
證明類似定理2.3,略.
推論2.1若T=T n⊕Z(T)且I?Z(T)是T的理想,則T是可限制的李三系?T/I是可限制的李三系.
證明充分性.根據(jù)定理2.2,結論顯然成立.
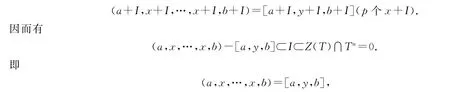
必要性.若T/I是可限制的李三系,則對任意x∈T n,?y∈Tn,滿足從而Tn是T的可限制的理想.而Z(T)是交換的,因而Z(T)是T的可限制的理想.又由于[Tn,Z(T),Z(T)]=0,[Tn,Z(T),T n]=0,因此根據(jù)定理2.4,T是可限制李三系.
定理2.5T是限制李三系(G,[p])的有限維子系,若λ:G×G→F是對稱雙線性的結合型,且λ在T×T上非退化,則T是可限制的李三系.
證明由黎茲表示定理知,對任意z∈T,都存在y∈T,使得f(z)=λ(y,z).對任意x∈T,z∈T,都存在y∈T,使得λ(x[p],z)=λ(y,z),即λ(x[p]-y,z)=0.又由于λ在T×T上非退化,因而x[p]-y=0.因此有
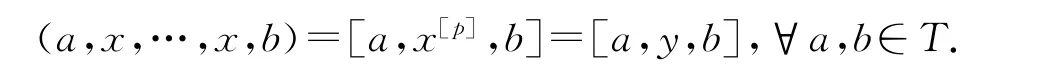
即T是可限制李三系.
[1]HODGE T L.Lie triple systems,restricted Lie triple systems and algebraic groups[J].Journal of Algebra,2001,244:533-588.
[2]HODGE T L.On the representation theory of Lie triple systems[J].Trans Amer Math Soc,2002,354:4359-4391.
[3]STRADE H,F(xiàn)ARNSTEINER R.Modular Lie algebras and their representations[M].New York:Monographs and Textbooks in Pure and Applied Mathematics,1988:80-100.
[4]董艷芹,張永正,孟凡洪.一類廣義模李超代數(shù)W-型模李超代數(shù)的導子[J].東北師大學報:自然科學版,2009,41(2):1-6.
[5]夏利猛,沈彩霞.具有非退化Killing型的余分裂李超代數(shù)[J].東北師大學報:自然科學版,2009,41(4):9-12.
[6]馬麗麗,張永正.M-階化廣義李超代數(shù)H(n)的導子超代數(shù)[J].東北師大學報:自然科學版,2010,42(4):6-11.
[7]溫啟軍,錢玲,陳良云.Jordan李代數(shù)的分解與Frattini理論[J].東北師大學報:自然科學版,2010,42(4):12-16.
Restrictable Lie triple systems
DONG Yan-qin1,2,TONG Shou-yu1,HUA Hong-tu1
(1.Department of Aviation,University of Air Force,Changchun 130022,China;2.School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China)
In the paper,restrictable Lie triple systems are defined.Second,the equivalence relation between restricted Lie triple systems and restrictable Lie triple systems is elaborated.Finally,it discusses the existence of restricted Lie triple systems by restrictable Lie triple systems.
Lie triple systems;restricted Lie triple systems;restrictable Lie triple systems
O 152.5
110·21
A
1000-1832(2011)03-0001-04
2010-05-04
國家自然科學基金資助項目(10871057,10701019).
董艷芹(1976—),女,講師,博士研究生,主要從事李代數(shù)研究.
陶 理)

