基于T-S模糊模型的新型非線性系統控制器設計
李麗芳,董秀娟,王 紅,張 友
基于T-S模糊模型的新型非線性系統控制器設計
李麗芳1,董秀娟2,王 紅3,張 友4
(1.吉林警察學院信息工程系,吉林長春 130117;2.東北大學信息科學與工程學院,遼寧沈陽 110006;3.齊齊哈爾大學數學系,黑龍江齊齊哈爾 161006;4.東北師范大學計算機科學與信息學院,吉林長春 130117)
針對非線性系統的鎮定控制問題,設計了一種新型的基于T-S模糊模型的非-并聯分布補償(PDC)控制器.在控制器設計的過程中,采用了一種新穎的模糊李亞普諾夫函數和一種松弛變量技術.這些措施的應用可以為控制器的設計引入更多的自由度,因而可以獲得比以往結果保守性更小的鎮定條件.由于控制條件是以線性矩陣不等式形式給出的,因此可以很方便地利用Matlab工具箱來進行求解.最后用一個仿真算例驗證了所提方法的有效性.
非-PDC控制律;T-S模糊模型;松弛變量技術;線性矩陣不等式
0 引言
現實世界中的絕大多數控制系統具有非線性特征,因而針對各種非線性系統所進行的穩定性分析和鎮定控制的研究具有非常大的研究意義和應用價值.自從上世紀80年代中期以來,T-S模糊模型[1]已經成為研究非線性系統的穩定性分析和控制設計問題的一種有力工具.由于T-S模糊模型被證明能夠以任意精度逼近定義在緊集上的一個連續非線性函數[2],因此從理論層面上保證了應用T-S模糊模型進行非線性系統問題研究的合理性.在基于T-S模糊模型的非線性系統鎮定控制研究中,文獻[3]提出了一種被稱為并聯分布補償(PDC)技術的模糊狀態反饋控制器設計方法,由此掀起了該研究方向的研究熱潮[4-8].通常情況下,應用這種PDC技術所得到的鎮定控制條件的保守性都非常大,這也大大限制了T-S模糊模型在該領域的應用.正是由于這個原因,文獻[4-8]在如何減少基于PDC技術的模糊控制系統鎮定控制條件保守性方面做了大量行之有效的研究工作.其中,文獻[4]首次通過引入附加變量技術把各個子系統之間的相互關系集中到一個增廣矩陣,得到了保守性較小的鎮定條件;文獻[7]應用Polya's定理得到了該問題的一種漸近充要條件,但是,該方法本身固有的缺點使得這種漸近充要條件在本質上仍然具有很大的保守性:其所采用的是普通的二次型李亞普諾夫函數,所得到的結果屬于常規的二次型鎮定控制條件.另一方面,模糊隸屬函數是T-S模糊系統的重要組成部分,在系統的鎮定控制設計過程中,如何將隸屬函數的信息考慮進去成為減少結果保守性的一條有效途徑[9-11].文獻[12]在利用模糊李亞普諾夫的基礎上,設計了一種非-PDC狀態反饋控制律,在設計過程中考慮模糊隸屬函數時間導數界這一有效信息,大大減少了已有結果的保守性.
本文設計了一種新型的非-PDC模糊系統狀態反饋控制器.特別是已有文獻中的非-PDC控制律可以被看做本文提出非-PDC控制律的一種特例.為了進一步減少結果的保守性,同時提出了一種新型的模糊李亞普諾夫函數和一種松弛變量技術.這些措施的實施使得在控制系統設計時能夠更有效的考慮隸屬函數的有用信息,得到比已有文獻保守性更小的鎮定控制條件.
1 預備知識
1.1 連續時間T-S模糊系統
首先考慮由如下模糊規則所描述的連續時間T-S模糊系統[1]:
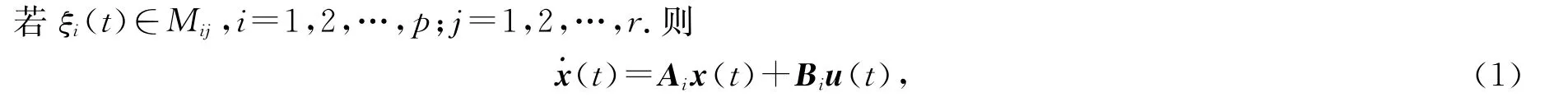
其中:x(t)∈Rn表示系統狀態變量;u(t)∈Rm為系統控制輸入信號;A i∈Rn×n,B i∈Rn×m;ξ1(t),…,ξp(t)為模糊系統前件變量;r表示模糊規則數,Mij(i=1,2,…,p;j=1,2,…,r)為模糊集.
該模糊控制系統的總體模型可以表示成:

在已有的模糊控制設計的文獻中,研究者們通過在設計中考慮模糊隸屬函數隨時間的導數信息來減少控制條件的保守性.通常給出如下假設條件:
假設1對于連續時間T-S模糊控制系統(1),設定其模糊隸屬函數的導數變換界滿足如下條件[12]:

這里λi為模糊建模時具體確定的實數.
文獻[12]給出了假設條件(4)在實際應用中的合理性與通用性,并且給出具體問題時λi的獲得方法.
1.2 放松性T-S模糊控制系統鎮定條件
文獻[12]給出了基于非-PDC控制律(3)的放松性T-S模糊控制系統鎮定控制條件,該條件具有比其先前文獻更小的保守性.

那么連續時間T-S模糊系統(1)在非-PDC控制律(3)控制下是漸近穩定的.
注釋1文獻[12]在系統設計中考慮了模糊隸屬函數信息(4),其所得鎮定控制的保守性比其先前文獻的要小;另一方面,非-PDC控制律(3)和模糊李亞普諾夫函數的使用也為保守性的減少做了很大貢獻.這也啟迪我們:如果從控制器的結構、模糊李亞普諾夫函數的選取、松弛變量的引入等方面進行進一步的優化設計,那么就有可能獲得保守性更小的T-S模糊系統鎮定控制條件.
2 主要結果
值得指出的是,已有文獻所得到的模糊控制系統鎮定控制條件的保守性還比較大,這也大大地限制了模糊控制的應用范圍.為了進一步減少控制條件的保守性,我們通過設計一種新型的非-PDC控制律和一個新穎的模糊李亞普諾夫函數,并且提出一種新的松弛變量技術,在系統設計中更加有效的考慮隸屬函數的有用信息,可以很大程度地減少了所得結果的保守性,進而擴大T-S模型的應用范圍.
設計如下形式的一種新型非-PDC控制律:
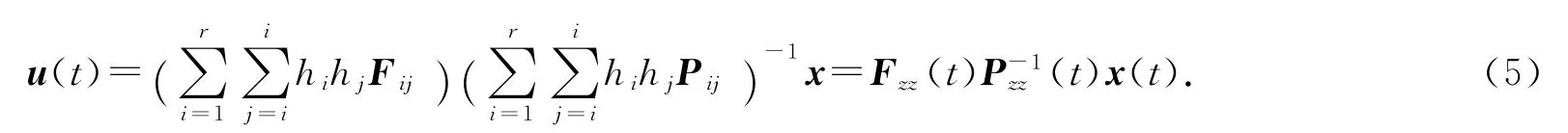
其中矩陣F ij和P ij表示待求的控制增益矩陣.把控制律代入T-S模糊控制系統(2),可以得到T-S模糊控制系統的閉環表示形式:


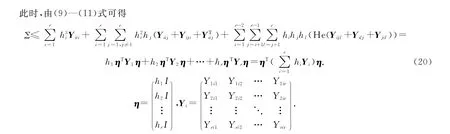
于是,若(12)式成立,那么Σ<0亦成立,也就是說閉環系統(6)是漸近穩定的.于是定理得證.
注釋2定理1通過設計新型的非-PDC模糊狀態反饋控制律(5)、模糊李亞普諾夫函數(13)和一種松弛變量技術的措施(引入了X和Y ijk等自由矩陣變量)得到了新的T-S模型系統鎮定控制條件(7)—(12).通過這些措施可以進一步減少結果的保守性.這一結論也會在下一節的仿真研究中得到驗證.
3 仿真例子
考慮由如下形式的連續時間T-S模糊系統:
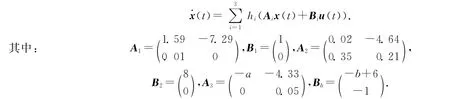
設置可調參數a,b以用來比較定理1與引理1[12]之間的保守性大小關系.
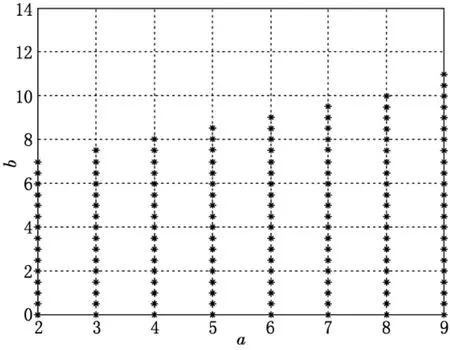
圖1 引理1的可行域
不失一般性,我們可以在同一假設條件(4)的情形下分別用定理1和引理1來求解可變參數a,b的可行范圍.用圖1和圖2分別給出它們所對應的鎮定控制可行域(星號表示可行點,其中假設條件(4)的λi選取為λi=1.0×10-2).從圖1和圖2的對比中很容易看出定理1的可行域大于引理1的可行域,也就是說,本文所提出的鎮定控制條件具有更小的保守性.
然后,選擇a=2,b=8.0,該點在圖1中是不可行點,但在圖2中是可行的,也就是說只有應用定理1才能使得該系統漸近穩定.求解線性矩陣不等式(7)—(12),可以獲取新型非-PDC模糊控制律(5)的系統控制增益矩陣.
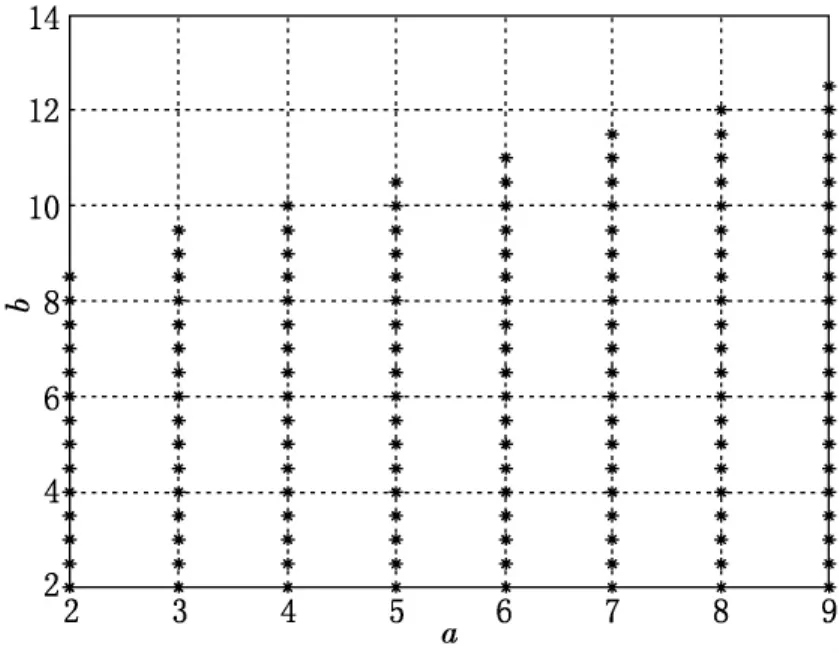
圖2 定理1的可行域

圖3 閉環系統狀態軌跡圖
給定系統初始值為x(0)=[1.2,-0.6]T,圖3給出了在所求得的控制器作用下系統的狀態軌跡圖象.可以看出在新型非-PDC控制器作用下閉環系統是漸近穩定的.
4 結語
本文給出了一種基于連續時間T-S模糊模型的非線性系統非二次鎮定控制設計的方法.通過提出新型的非-PDC控制律、新穎的模糊李亞普諾夫函數和松弛變量技術,大大減少了所得結果的保守性.從仿真結果可以看出本文所提的方法是有效的.
[1]TAKAGI T,SUGENO M.Fuzzy identification of systems and its application to modeling and control[J].IEEE Transactions on Syst Man Cybern,1985,15:116-132.
[2]FENG G,GAO S,REES W.An approach toH∞control of a class of nonlinear systems[J].Automatica,1996,32(10):1469-1474.
[3]WANG H,TANAKA K,GRIFFIN M.An approach to fuzzy control of nonlinear systems:stability and design issues[J].IEEE Transactions on Fuzzy Systems,1996,4(1):14-23.
[4]TANAKA K,IKEDA T,WANG H.Fuzzy regulators and fuzzy observers:relaxed conditions and LMI-based designs[J].IEEE Transactions on Fuzzy Systems,1998,6(2):250-265.
[5]KIM E,LEE H.New approaches to relaxed quadratic stability conditions of fuzzy systems[J].IEEE Transactions on Fuzzy Systems,2000,8(5):523-534.
[6]LIU X,ZHANG Q.New approaches toH∞controller designs based on fuzzy observers for T-S fuzzy systems via LMI[J].Automatica,2003,39(9):1571-1582.
[7]TEIXEIRA M,ASSUNCAO E,AVELLAR R.On relaxed LMI-based designs for fuzzy regulators and fuzzy observers[J].IEEE Transactions on Fuzzy Systems,2003,11(5):613-622.
[8]SALA A,ARINO C.Asymptotically necessary and sufficient conditions for stability and performance in fuzzy control[J].Fuzzy sets and Syetms,2007,158(24):2671-2696.
[9]SALA A,ARINO C.Relaxed stability and performance conditions fot T-S fuzzy systems with knowledge on membership function overlap[J].IEEE Transactions on Syst Man Cybern Part B,2007,37(3):727-732.
[10]MOZELI L A,PALHARES R M,SOUZA F O,et al.Reducing conservativeness in recent stability conditions of T-S fuzzy systems[J].Automatica,2009,45(6):1580-1583.
[11]LAM H K.Stability analysis of T-S fuzzy control systems using parameter-dependent Lyapunov functions[J].IET Control Theory and Applications,2009,3(6):750-762.
[12]TANAKA K,OHTAKE H,WANG H O.A descriptor system approach to fuzzy control system design via fuzzy Lyapunov functions[J].IEEE Transactions on Fuzzy Systems,2007,15(3):333-341.
Novel control synthesis of nonlinear systems based on the T-S fuzzy model
LI Li-fang1,DONG Xiu-juan2,WANG Hong3,ZHANG You4
(1.Department of Information Engineering,Jilin Police College,Changchun 130117,China;2.School of Information and Engineering,Northeast University,Shenyang 110006,China;3.Department of Mathematics,Qiqihar University,Qiqihar 161006,China;4.College of Computer Science and Information Technology,Northeast Normal University,Changchun 130117,China)
A new kind of non-PDC control scheme has been proposed for dealing with the problem of stabilizing nonlinear systems based on the Takagi-Sugeno fuzzy model.Both a novel fuzzy Lyapunov function and a slack variable technique have been applied in the process of control synthesis.Because more freedom could be introduced in virtue of the above measures,the obtained stabilization condition is less conservative than before.Indeed,all the results proposed in this paper are in terms of linear matrix inequality which is easy to be solved by using the Matlab tools.Finally,a numerical example is also provided to illustrate the effectiveness of the proposed approaches.
Non-PDC control scheme;T-S fuzzy model;slack variable technique;linear matrix inequality
TP 273
120·3040
A
1000-1832(2011)03-0054-06
2011-03-16
國家自然科學基金資助項目(10971021).
李麗芳(1970—),女,副教授,主要從事控制論與數學教法研究;通訊作者:張友(1971—),男,博士,副教授,主要從事控制論與模式識別研究.
陶 理)

