海岸線長度量算方法的研究

劉春杉，王華接，沈亮

（ 廣東省海洋與漁業環境監測中心，廣東 廣州 510222 ）

海岸線長度量算方法的研究

劉春杉，王華接，沈亮

（ 廣東省海洋與漁業環境監測中心，廣東 廣州 510222 ）

海岸線是重要而寶貴的自然資源，準確量算海岸線長度是摸清海洋家底和實施有效管理的前提。但目前海洋界沒有統一的海岸線長度量算方法。提出基于高斯平均引數的橢球面長度算法，并采用MapBasic語言的實現海岸線長度的自動化計算，通過驗證和比對，比目前海洋界普遍采用的平面長度算法更準確，可在實際工作中推廣。

海岸線；橢球面長度算法；高斯平均引數

1 背 景

海岸線是重要而寶貴的戰略資源，既是港口、旅游、養殖等海洋產業發展重要載體，也是海洋生態多樣性重要的來源，具有一定的稀缺性和不可再生性質。通過對海岸線的有效管理，合理利用海岸線，并使其發揮最大的社會經濟效益，對于當前面臨經濟結構調整和產業結構升級的廣東省來說，具有重要的現實意義。

海岸線位置和長度是海洋綜合管理的重要基礎數據，準確計算海岸線長度，是摸清海洋資源家底和實現對海岸有效管理的前提。近年來，受自然和人為因素的影響，海岸線變化較大，20世紀 80年代進行的“全國海岸帶和海涂資源綜合調查”中的海岸線數據資料已不能反映當前我國海岸線的現狀，不宜再作為現實管理和規劃制訂的依據，有必要重新測量海岸線位置并計算其長度。2003年起，國家海洋局啟動了“我國近海海洋綜合調查與評價專項”（簡稱“908”專項），專項要求對海岸線重新做了修測，測量最新的海岸線位置并計算其長度。

與以往大規模調查不同，本次海岸線修測基于WGS84坐標系，采用GPS實測與遙感影像提取相結合的先進技術手段，對于可以到達的海岸，順直海岸每隔50 m定一個點，曲折海岸適當加密，采用 RTK-GPS實測海岸線；對于難以到達的海岸，則采用 1︰10000比例尺地形圖矢量化后的數據與2005年的SPOT遙感影像數據疊加擬合、修正、提取海岸線。最終兩者通過GIS系統拼接合并成為完整而連續的海岸線矢量數據。

應該說明的是，海岸線的長度沒有一個公認的準確測量方法。按照分形理論，采用不同的測量精度，設置不同的步長，所得出的海岸線長度值都不相同，理論上海岸線可以無限長。本文所討論的內容是選擇更準確的算法，對已經測量好，并采用計算機存貯的海岸線矢量數據進行長度計算。

2 問題的提出

傳統的地圖上曲線長度的量算包括兩腳規法、曲線計法、貼銅絲法等，都是在圖紙上借用相應的設備進行手工量算，受圖紙的保存程度、比例尺、投影以及手工操作誤差影響較大。目前，地圖、測繪等領域都進入了數字時代，地圖上的曲線如海岸線等都是按照節點順序，以節點坐標的形式貯存在計算機中，通常稱之為矢量數據，而地圖上曲線長度量算已轉化為對曲線矢量數據的長度量算。

海岸線矢量數據能夠準確的描述海岸線的位置，但其長度值卻有多種量算方法，不同的方法可以得出不同的長度值。在此次海岸線修測中，國家制訂了《海岸線修測技術規程》，規程中提出：“在1︰50 000專題圖上進行海岸線長度量算”、“圖件的坐標系采用 WGS-84，高斯-克呂格投影”，但規程并未提出具體的長度量算方法。

目前，我國海洋管理部門和海洋研究部門多采用高斯-克里格投影下的平面長度算法來計算海岸線長度。這種算法存在缺陷，在短距離、小范圍情況下使用時誤差不大，但對于“成千上萬”公里的海岸線來說，累積誤差過大。今后應采用更接近實際長度的橢球面長度算法，來計算海岸線長度。

3 量算方法的比選

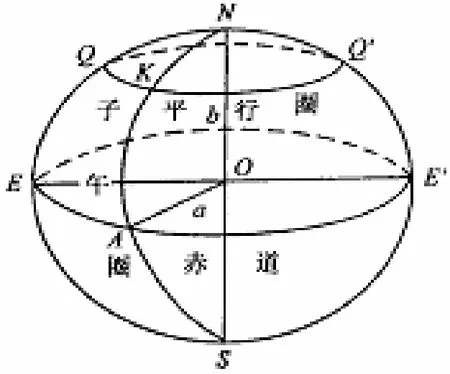
圖 1 地球橢球體Fig. 1 Earth ellipsoid

為了測量成果的計算和制圖工作的需要，通常選用一個同大地體相近的，可以用數學方法來表達的旋轉橢球體來代替地球。這個旋轉橢球是一個橢球繞其短軸旋轉而成，其表面成為旋轉橢球面。

如圖 1所示，地心距赤道的距離為長半軸（a=OA），地心距南北極點（S、N）的距離為短半軸（b=ON），每一個緯圈都為圓，每一個經圈都為橢圓（a為長半軸，b為短半軸）。

海岸線可以看作是附著在地球表面的曲線，對于這種曲線的長度，可以兩種類型的量算方式，一種是橢球面按一定算法投影到平面上，然后計算節點間的平面距離并累積而求得曲線長度，簡稱為平面長度算法，另一種是不經投影，直接從地球表面計算節點間的距離并累積求得曲線長度，簡稱為橢球面長度算法。

3.1 高斯-克里格投影下的平面長度算法

高斯投影是普遍應用于大、中比例尺的地形圖制圖的一種投影，也是海岸線修測規程所要求的成圖投影。高斯投影下的平面長度算法為先計算相鄰節點間的平面距離，再對曲線中所有相鄰節點距離進行累加，得出曲線長度。計算公式為：

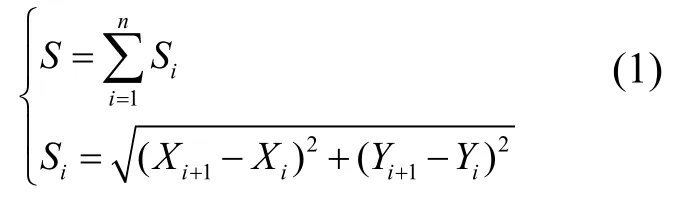
S：曲線線段長度

Si：相鄰節點間連線長度

Xi，Yi：節點橫軸和縱軸平面坐標值

作為等角投影的一種，高斯投影存在長度變形的情況，變形公式為：

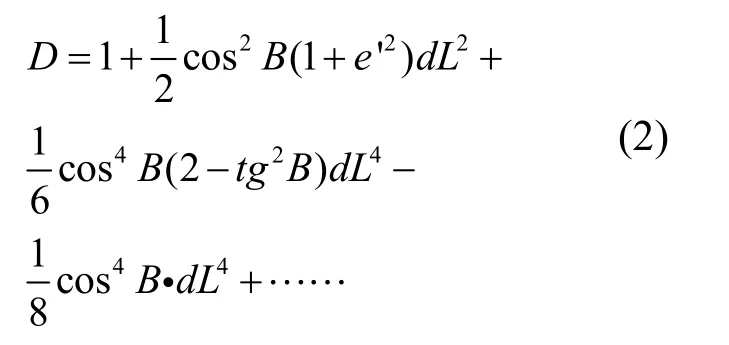
D為變形比，e’為地球的第二偏心率，B為緯度，dL為距中央經線的經度差。

從公式可知，即在東西方向上，距中央經線越遠，長度變形越大，中央經線上無變形；在南北方向上，離赤道越近，變形越大，南北兩極無變形。

廣東省位于低緯度地區，東西跨度超過 8°。按照高斯投影6°分帶，全省沿海分屬兩個投影帶，按照3°分帶，則全省沿海分屬3個投影帶。故若按照高斯投影下的平面長度量算方法，則廣東省的海岸線長度的累計誤差較大。

3.2 橢球面長度算法

與平面長度算法相同，橢球面長度算法也分為2步，即先計算相鄰節點間距離，再對所有相鄰節點間的距離進行累加。

橢球面上2點間的距離可以有不同的算法，可以計算過2點的大圓劣弧長度，可以計算2點間的法截弧長度，也可以計算2點間的大地線長度。

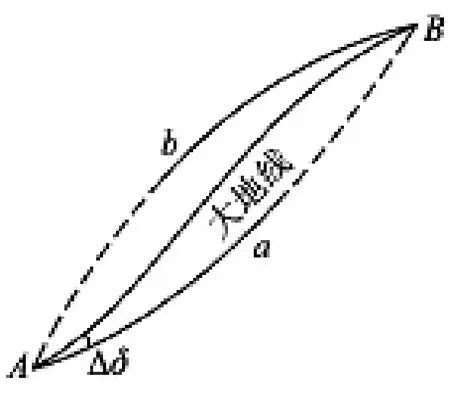
圖 2 大地線Fig. 2 Geodesic

按照大地測量學，橢球面上兩點間的最短程曲線叫做大地線（又稱測地線，如圖 2所示）。本文所述的橢球面長度算法，即通過計算海岸線上所有相鄰節點間的大地線長度，再累加得出曲線長度。采用橢球面長度算法有3大好處：

第一，由于大地線是兩點間惟一最短線，因此由相鄰節點間大地線累計的曲線長度更為準確；

第二，由于大地線的長度值取決于兩點的經緯度和橢球體的長、短半軸，與投影無關，可以保證曲線在不同投影下長度值的一致性；

第三，對于經度跨度大的曲線來說，采用橢球面長度算法，算法更為簡單，可以避免平面長度算法中因跨帶而需要將完整的曲線分解成不同投影帶的線段，并變換中央經線等參數才能較為準確計算的麻煩。

通過已知2點，計算兩點間的大地線長度稱為大地主題反算（與大地主題正算合起來統稱大地主題解算）。據不完全統計，大地主題解算方法有 70多種，其中適用于短距離的量算的有高斯平均引數法，適用于中長距離量算的有貝塞爾公式以及由它派生的公式，考慮到本次海岸線相鄰節點間距離一般不超過1 km，而高斯平均引數法解算公式結構雖然復雜，但精度比較高，反算無需迭代，方便計算機編程，因此本文采用高斯平均引數法進行大地主題反算。

4 橢球面長度算法的實現

4.1 相鄰節點距離量算

假設地球表面有兩點P1，P2（如圖3所示），設 S 為 P1，P2兩點間大地線長度，（L1，B1），（L2，B2）分別為2點的經緯度坐標。

圖 3 橢球面長度Fig. 3 Ellipsoid-Length

按照高斯平均引數正算公式，可推導出高斯平均引數反算公式3：

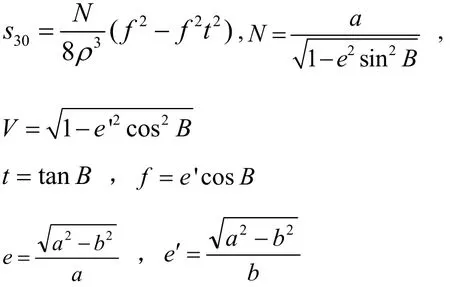
其中 a，b分別為橢球體的長半軸和短半軸。其值采用WGS84橢球體的參數。

最后，由三角函數可得公式5:

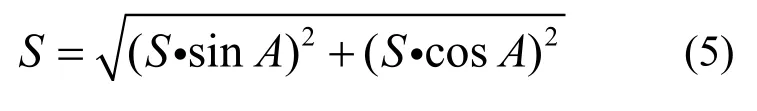
將公式4代入到公式5即可計算兩點間的大地線長。

為方便海岸線長度的量算，作者采用了可直接讀取海岸線各節點坐標值的MapBasic7.0（MapInfo的附屬開發包）編程實現曲線長度的自動化計算。代碼主要包括兩點間的距離量算和曲線中各節點間距離的累計。

兩點間的距離量算核心代碼為：

4.2 曲線長度計算

在曲線中按順序將節點歷遍，計算相鄰兩節點間的距離（大地線長），并且累加。

核心代碼為：

5 驗 證

在地球橢球面上，赤道圈為大圓，半徑為地球長半軸，子午圈為橢圓，長、短半軸與地球的長、短半軸一致。按照大地測量理論，赤道線上任意 2點間的球面距離為這兩點間的赤道劣弧長，同樣子午線上任意2點間的球面距離為2點間的子午劣弧長。由于子午圈弧長和赤道弧長都有現成的精確計算公式，可求取準確長度，因此在子午圈和赤道上各截取2段曲線作為橢球面長度算法和平面長度算法的驗證。

由對照表1可知，采用公式4、5所得出的地球表面曲線長度是準確的，算法是可信的。

表 1 子午弧長和赤道弧長驗證結果對照表（單位：m）Tab. 1 Results table of latitude and equatorial arc length (unit: m)

6 算 例

如圖4所示，曲線AE為廣東、香港、澳門的大陸海岸線，西至109.685°E，東至117.191°E。用 112.5°E、114°E、115.5°E 3條經線與曲線AE相交，分別得到B、C、D 3個交點。

按照高斯投影6°分帶，廣東沿海位于19、20兩個投影帶，其中曲線AC位于19投影帶，中央經線為111°E；曲線CE位于20投影帶，中央經線為117°E。

按照高斯投影3°分帶，廣東沿海位于37、38、39三個投影帶，其中曲線AB位于37投影帶，中央經線為111°E；曲線BD位于38投影帶，中央經線為114°E；曲線DE位于39投影帶，中央經線為117°E。

按照平面長度算法和橢球面長度算法，分別對曲線AE、AC、CE、AB、BD、DE進行長度測量，對照結果見表2。

表 2 橢球面長度與平面長度計算結果對照表（單位：m）Tab. 2 Result comparison of ellipsoid-length and plane-length (unit: m)

圖 4 廣東省海岸線示意圖Fig. 4 Guangdong coastline

對照結果表明：采用平面長度算法與橢球面長度算法差別并不大，當海岸線長度較短時，兩者算法所得結果相近；但當量算對象長度足夠長時（如廣東省海岸線超過4 000 km），平面長度算法與橢球面長度算法所得出的結果誤差絕對值較大。

7 結 論

從驗證和算例的結果來看，本文推薦采用的基于高斯平均引數算法的橢球面長度計算方法理論是合理的，算法是可信的，比平面長度算法結果更準確，可在今后海岸線長度量算工作中推廣應用。

[1] 孔詳元. 大地測量學基礎 [M]. 武漢: 武漢大學出版社, 1996:30-45.

[2] 張力果. 地圖學（第二版）[M]. 北京: 高等教育出版社, 1991:56-73.

[3] Beno?t Mandelbrot. How Long Is the Coast of Britain? [J]. Science,1967, 156(3775): 636-638.

[4] 李炳亞. 灘涂面積及海岸線長度計算方法 [J]. 遙感信息, 1987, 2:34-36.

[5] 周振宇, 郭廣禮, 賈新果. 大地主題解算方法綜述 [J]. 測繪科學, 2007, 32(4): 190-191.

[6] 趙長勝. 高斯平均引數計算大地坐標主題反解的迭代算法 [J].測繪通報, 2004, 10: 11-12.

[7] 丁佳波. 海圖上計算海岸線長度和海區面積的投影計算方法 [J].地圖, 1996, 02: 67-68.

[8] 林桂蘭, 鄭勇玲. 海岸線修測的若干技術問題探討 [J]. 海洋開發與管理, 2008, 7: 61-67.

[9] 劉仁釗, 伍吉倉. 任意精度的子午線弧長遞歸計算 [J]. 大地測量與地球動力學, 2007, 27(5): 59-62.

[10] 嚴伯鐸. 橢球子午線弧長的一種計算方法 [J]. 地礦測繪, 2003,19(3): 7-10.

Study on the coastline length calculation methods

LIU Chun-shan, WANG Hua-jie, SHEN Liang

(Guangdong Ocean and Fishery Environment Monitoring Center, Guangzhou 510222, China)

Coastline is the important and valuable natural resource, and accurate calculation of the coastline length is the premise of understanding the status of marine resources, and effective management of coast. But there is no uniform method of calculating the length of the coastline. This paper proposes using Ellipsoid-Length algorithm based on Gauss mid-latitude formula to calculate the length of the Earth's surface curves, and running MapBasic programming to automatically get the length. Through the verification and comparison, the results show that Ellipsoid-length algorithm is more accurate than Plane-Length algorithm, and worth the promotion in future work.

coastline; Ellipsoid-Length algorithm; Gauss mid-latitude formula

P229.2

A

1001-6932(2011)05-0481-06

2010-07-15；

2010-08-25

我國近海海洋綜合調查與評價專項（908專項）。

劉春杉 ( 1976－)，男，工程師，主要從事海洋測量和信息化建設。電子郵箱：lcs158@gmail.com。