關于不定方程x2+4n=y5

崔保軍

(甘肅民族師范學院數學系，甘肅合作 747000）

關于不定方程x2+4n=y5

崔保軍

(甘肅民族師范學院數學系，甘肅合作 747000）

用代數數的方法證明了不定方程 x2+4n=y5僅有解(n，x，y)=(5m，0，4m)，(5m+2，±25m+2，2·4m).

不定方程;整數解;整環

設A，B∈N，A無平方因子，關于不定方程:

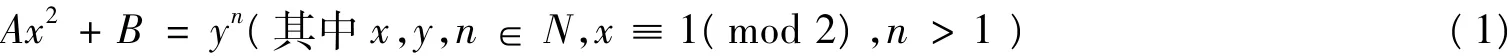
的解的討論是數論中的一類重要課題.當 A=1，B=1時，Lebesgue［1］證明了(1)無整數解.Nagell［2］證明了當A=2，B=1，n=5時，方程(1)僅有整數解(x，y)=( ±11，3).文獻［3］給出了 x2+4n=y3在 2|n 時的整數解.本文利用代數數論的方法證明了不定方程 x2+4n=y5僅有解(n，x，y)=(5m，0，4m)，(n，x，y)=(5m+2，±25m+2，2·4m).為此，先引入引理

引理1 不定方程2m－1=5z2僅有解m=0，z=0;不定方程2m+1=5z2僅有解m=2，z=1.

證明:對于不定方程2m－1=5z2，若m≥2，兩邊取mod 4，得－1≡1(mod 4)，可知此時方程無解;m=1時也無解.故該方程僅有解m=0，z=0.

同理可證不定方程2m+1=5z2僅有解m=2，z=1.

引理2［4］設 M 是唯一分解整環，正整數 k≥2，以及 α，β∈M，(α，β)=1，那么若 αβ = γk，γ∈M，則有 α=ε1μk，β =ε2νk，μ，ν∈M，其中 ε1，ε2是 M 中的單位元素，并且 ε1ε2=εk，ε 為單位元素.

定理1 不定方程:

僅有解(n，x，y)=(5m，0，4m)，(5m+2，±25m+2，2·4m)(m∈N).

證明 首先考慮x≡1(mod 2)的情況.在Z［i］中式(2)可以寫為(x+2ni)(x－2ni)=y5，x，y∈N.設 δ=(x+2ni，x －2ni)，由 δ|(2x，2·2ni)=2，知 δ只可能是1，1+i，2.因 x≡1(mod 2)知 x+2ni≡1(mod 2)，所以δ≠2:如果 δ≠1+i，則 N(1+i)|N(x+2ni)，即2|x2+4n，但 x≡1(mod 2)，產生矛盾.因此 δ=1，由此及引理2知:

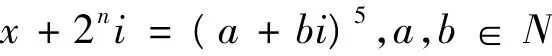
因而有:

由式(4)有 b= ±1，±2t，±2n，其中 t∈N，1≤t≤n －1.以下就 b的取值情況分別討論方程(2)得解.

若 b= ±1，則 ±2n=5a4－10a2+1，即5(a2－1)2=4±2n.因2|4 ±2n，此時有 a=0 或 a≡1(mod 2)，由式(4)推得x≡0(mod 2)，這與x≡1(mod 2)矛盾.

若 b= ±2t，則有 ±2n－t=5a4－10a24t+42t，即4·42t±2n－t=5(a2－4t)2，此時必有 a≡0(mod 2)，得到 x≡0(mod 2)，這也與x≡1(mod 2)矛盾.

若b= ±2n，則有±1=5a4－10a24n+42n，即4·42n±1=5(a2－4n)2，由引理1可知此時方程也無解.

再考慮x≡0(mod 2)的情況，此時y也是偶數.由對x≡1(mod 2)的情況的討論知，只需考慮(x，4n)=2n.

1)若 n=5m，令 x=25mx1，y=4my1，則方程(2)變為 x21+1=y51.由對 x≡1(mod 2)，n=0 的討論知必有 x1=0.推知此時方程(2)僅有解 x=0，n=5m，y=4m.

2)若 n=5m+1，令 x=25m+1x1，y=2·4my1，則方程(2)變為 x21+1=8y52，由于 x1為奇數，取 mod 8，知此時方程(2)無解.

3)若 n=5m+2，令 x=25m+2x1，y=2·4my1，則方程(2)變為:

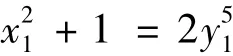
根據文獻［4］上面的結果可寫成 x1+i=(1+i)(a+bi)5，x1，a，b∈Z.

即1=a5+5a4b－10a3b2－10a2b3+5ab4+b5=(a+b)［(a+b)4－20a2b2］.

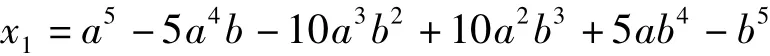
有第一式知 a+b= ±1，(a+b)4－20a2b2= ±1，因而必有 ab=0，由此解出 a=0，b=1;a=1，b=0，在由第二式知x1= ±1，進而得到方程(2)的解為n=5m+2，x= ±25m+2，y=2·4m.

4)若 n=5m+3，令 x=25m+3x1，y=4m+1y1，則方程(2)變為 x21+1=16y51.由……