基于粒子群算法的關鍵鏈多項目調(diào)度管理

林晶晶，周國華

（西南交通大學a.公共管理學院，b.經(jīng)濟管理學院，成都 610031）

0 引言

關鍵鏈項目管理方法是將約束理論成功應用于項目管理領域而產(chǎn)生的一種全新的項目計劃調(diào)度方法[1]。約束理論是Goldratt于20世紀70年代末期基于OPT系統(tǒng)發(fā)展起來的。該理論認為系統(tǒng)的制約因素決定系統(tǒng)的有效產(chǎn)出。因此，將管理重點放在系統(tǒng)的制約因素上，通過改進制約因素達到最大的有效產(chǎn)出。以TOC為理論基礎所提出的關鍵鏈方法自產(chǎn)生之初便引發(fā)了企業(yè)界和學術界的廣泛關注，被認為是21世紀項目管理領域的一個重大突破，并成為項目管理領域的研究熱點問題[2,3]。

目前關于關鍵鏈項目管理的研究大都基于單項目環(huán)境，對關鍵鏈方法進行理論基礎的分析和探討[1-3]，在此基礎上對關鍵鏈的識別和緩沖區(qū)的設置展開研究[4,5]。相關文獻的研究表明，采用CCPM能有效地降低項目受不確定性因素影響的程度和改善項目計劃，并已在進度、成本、范圍和績效管理等方面獲得了成功應用[4]。

近年來，關鍵鏈方法運用于多項目管理的研究較少，大都從定性的角度開展了研究[5～9]。在定量方面，目前的研究主要集中于瓶頸資源約束下多項目工序的排序[10,11]。本文基于現(xiàn)有研究成果，探討單瓶頸資源約束下關鍵鏈在多項目中應用的理論基礎，考慮不同項目的重要性及項目完工提前或滯后的獎懲，研究滿足系統(tǒng)總收益最大化目標的瓶頸資源分配計劃；并將粒子群算法引入到關鍵鏈多項目管理的優(yōu)化問題中，以期提供一個新的解決思路。

1 關鍵鏈方法

1.1 關鍵鏈方法在單項目環(huán)境中的應用

關鍵鏈方法是將約束理論成功應用于項目管理領域而產(chǎn)生的一種全新的項目計劃調(diào)度方法。約束理論（Theory of Constraints，TOC）是Goldratt于20世紀70年代末期基于OPT系統(tǒng)發(fā)展起來的，認為系統(tǒng)的制約因素決定系統(tǒng)的有效產(chǎn)出。因此，將管理重點放在系統(tǒng)的制約因素上，通過改進制約因素達到最大的有效產(chǎn)出。

作為TOC在項目管理中直接應用產(chǎn)生的關鍵鏈方法與關鍵路徑方法不同的是，強調(diào)制約項目周期的是關鍵鏈而非關鍵路徑，關鍵鏈是既考慮工作間的依賴關系又考慮資源間依賴關系的最長的工作序列。Goldratt認為由于項目存在的不確定性和墨菲定律，在估計項目持續(xù)時間時，通常會在每個工序上都加入安全時間。但實際上，由于學生綜合癥及帕金森定律、多任務以及工作間的依存關系等多種因素的存在，工序上加入的安全時間常常被浪費，導致項目工期拖延。因此，基于工序工期呈正態(tài)分布的假設，Goldratt提出以50%可能完成的時間作為工序工期的估計，并以此建立工作網(wǎng)絡圖；同時考慮工序間緊前關系約束和工序間的資源約束來確定關鍵鏈，如果存在多條關鍵鏈就任意選擇一條。然后通過項目緩沖、輸送緩沖和資源緩沖機制來消除項目中不確定因素對項目計劃執(zhí)行的影響，保證在確定環(huán)境下編制的項目計劃在動態(tài)環(huán)境下的順利執(zhí)行和關鍵鏈所需資源能夠及時獲取。

1.2 關鍵鏈方法在多項目管理中的應用

關鍵鏈多項目進度管理方法不僅能夠很好減弱項目間的關聯(lián)效應和不確定因素的影響，消除項目成員的不良工作行為，縮短項目的工期，而且能夠較有效地解決項目間的資源沖突，改善多項目的執(zhí)行環(huán)境[9]。由于TOC方法在單項目與多項目環(huán)境下的應用各有側(cè)重點[7]，因此也決定了關鍵鏈在單項目與多項目中應用的不同。（見表1）

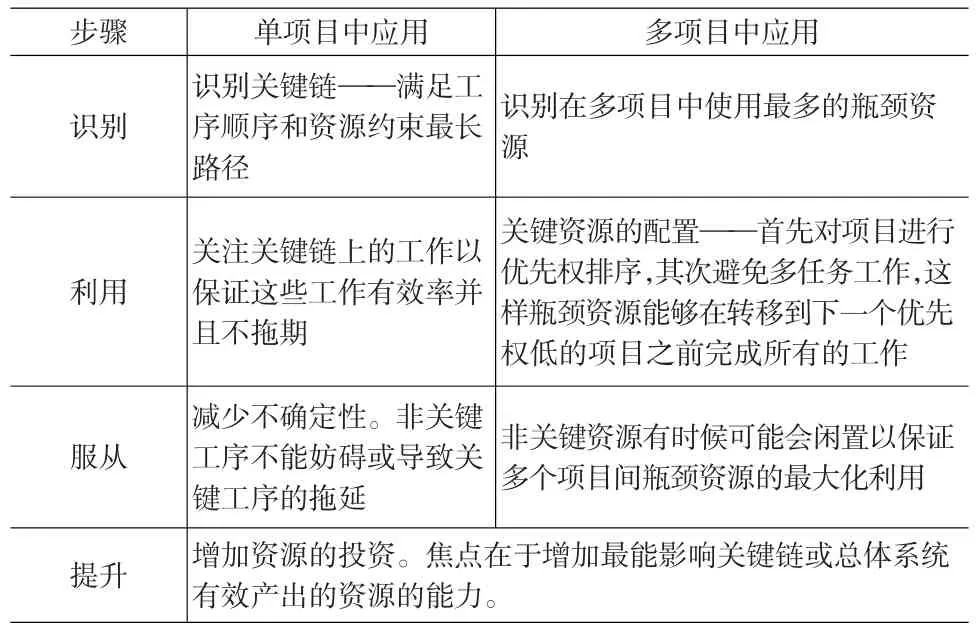
表1 TOC在單項目與多項目應用時的不同[7]

從表1可以看出，關鍵鏈方法在單項目和多項目領域的應用有側(cè)重點。Goldratt認為，在多項目環(huán)境中，關鍵的是要關鍵鏈用TOC的角度來解決這個問題[1]，核心方法是采用系統(tǒng)的思考，識別系統(tǒng)發(fā)展的瓶頸，在各個項目之間協(xié)調(diào)好資源，盡量減小資源的瓶頸。Goldratt博士提出的關鍵鏈多項目管理的步驟如下。

步驟1：設定各個項目的優(yōu)先權；

步驟2：按關鍵鏈方法計劃和調(diào)度每個項目；

步驟3：交錯各個項目，避免資源沖突；

步驟4：設定各項目緩沖及每個項目的輸送緩沖；

步驟5：對緩沖區(qū)進行有效管理。

雖然提出了以上5個步驟，但是Goldratt對這些驟如何具體實施并沒有涉及。現(xiàn)有關于關鍵鏈多項目管理的文獻也大都基于以上5個步驟進行討論。

關鍵鏈方法在多項目中應用的文獻還相對較少，對于瓶頸資源的識別與分配，對于瓶頸緩沖的性質(zhì)與設置方法還未有統(tǒng)一的、成熟的方法。本論文主要通過對以上問題進行分析，著重對存在較大爭議的步驟3——交錯各個項目，避免資源沖突進行研究，建立單瓶頸資源約束下的關鍵鏈多項目調(diào)度模型。

2 瓶頸資源約束下的多項目總收益最大化模型

2.1 問題描述與前提假設

在一個多項目環(huán)境中，存在N個相互獨立的并行項目，每個項目用Qi表示(i=1,2,3…N）。由于有一種瓶頸資源出現(xiàn)多任務情況，每個項目中僅有一個任務使用，且這些任務發(fā)生在關鍵鏈上，排除林晶晶（2008）考慮的特殊情況。由于發(fā)生瓶頸資源的爭奪，因此瓶頸資源在多任務中使用的先后順序直接影響著不同項目的完工時間。考慮合同交付期的法定效力，瓶頸資源先分配的任務所在項目能夠盡快完工，若有提前，將按合同條款給予相應的獎勵，后分配到瓶頸資源的任務所在項目可能發(fā)生延誤，也將按合同條款進行處罰。筆者認為，系統(tǒng)中的重要項目，在發(fā)生拖延時，除了造成直接的經(jīng)濟成本上的損失，還會對組織的聲譽、戰(zhàn)略等造成其他無形的損失。同理，重要項目若能提前完工，除了按照合同規(guī)定獲取一定的獎勵，還會帶來額外的收益。所以在建模時考慮利用重要性級數(shù)k對成本損失與獎勵進行加權，將隱性的損失和獎勵量化。

為確定本文分析的背景，需要進行如下假設：

（1）基于約束理論的關鍵鏈方法在應用到多項目系統(tǒng)時，要求制約系統(tǒng)績效的瓶頸資源在使用過程中不間斷，以保證資源利用率的最大化。

（2）不考慮項目對其他非瓶頸資源的共享，并假設其他非瓶頸資源的供應量是充分的。

（3）瓶頸資源為可更新的有限離散資源。

（4）不考慮瓶頸資源從一個項目到另一個項目的準備時間；所有資源在工序中的使用一旦開始就不能中斷，必須等到工序結(jié)束后才能轉(zhuǎn)入其他工序。

（5）瓶頸資源不能通過外部租借或購買等方式獲取。

此外，模型中出現(xiàn)各符號的具體指代如下：

Δi為項目i因為瓶頸資源約束造成的延誤時間；

index為瓶頸資源在不同項目中的使用順序的序列；

Pi為前一個使用瓶頸資源的項目編號，其中，Pi=index(j-1),j=2,3,…N；

R為瓶頸資源在每個階段的可用量；

r為每個瓶頸資源；

Δci為項目Qi每拖延一天的成本損失；

Δei為項目Qi每提前一天完工，所能得到的獎勵；

ki為項目Qi的重要性級數(shù)，ki越大項目越重要；

Tsi為項目Qi的合同交付期；

Tai為項目Qi的實際完工期；

ti為項目Qi中使用瓶頸資源工序的作業(yè)時間。

2.2 瓶頸資源約束下的多項目系統(tǒng)總收益最大化目標模型的建立

基于以上假設和本研究的中心思想，可以建立如下瓶頸資源分配模型

本文所探討的目標函數(shù)是多項目系統(tǒng)總收益的最大化，見式（1），不僅考慮項目實際完成時間與合同交付期的差異造成的獎懲，還考慮不同項目的重要性。為了保證關鍵鏈多項目管理思想所提出的瓶頸資源使用的連續(xù)性，要求后一個使用瓶頸資源的工序的開始時間等于前一個使用瓶頸資源工序的完成時間，見約束條件（2）。index(j)表示資源分配順序方案中，第j個分配到瓶頸資源的項目編號，第1個分配到瓶頸資源的項目可以按時完工，不會因資源短缺造成工期延誤，因此有約束條件（3）。約束條件（4）說明了瓶頸資源的總量限制。

3 多項目總收益最大化模型的粒子群算法設計

3.1 粒子群算法

粒子群優(yōu)化（PSO）算法由于其簡單性與有效性，在它被提出后不久，就引起了許多研究者的廣泛關注，并得到了迅速發(fā)展。該算法源于對鳥群覓食等社會行為的模擬研究。作者最初的設想是通過仿真簡單的社會系統(tǒng)，研究并解釋復雜的社會行為，后來卻發(fā)現(xiàn)從中可以提煉出一種解決復雜問題的有效優(yōu)化算法。

PSO算法利用Np個粒子（個體）組成的粒子群在N維問題空間中以迭代的方式搜索最優(yōu)解。粒子在問題空間中飛行，具有位置與速度兩個特征，其中粒子位置對應問題的潛在解。粒子i具有記憶功能，可以記錄下自己在飛行過程中曾經(jīng)歷過的最優(yōu)位置（稱為個體最優(yōu)位置pi）及所有粒子曾經(jīng)歷過的最好位置（稱為全體最優(yōu)位置pg）。每次迭代中，粒子i第j維的速度vij與位置xij按下面的表達式更新

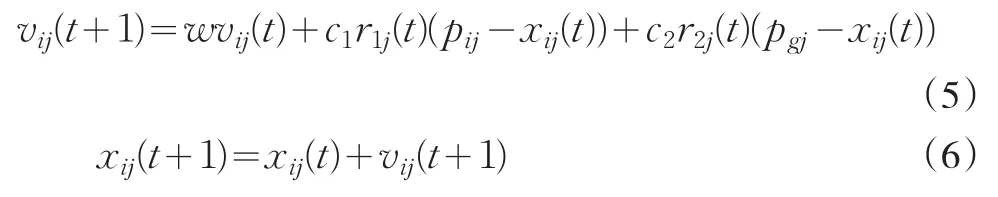
其中，t為迭代次數(shù)；i=1,……,Np；j=1,…… N；w為慣性權，c1和c2為加速系數(shù)，r1j和r2j為在[0,1]內(nèi)均勻分布的隨機數(shù)。式（5）等號右邊由3部分組成，第1部分為“慣性”部分，表示粒子保持先前的速度；第2部分是粒子跟蹤自己歷史最優(yōu)值的權重系數(shù)，表示粒子自身的認識，所以c1又稱為認知系數(shù)；第3部分是粒子跟蹤群體最優(yōu)值的權重系數(shù)，表示粒子對整個群體知識的認識，體現(xiàn)粒子間的信息共享與相互合作。所以c2又稱為社會系數(shù)。

在PSO算法，粒子速度vi的最大值一般被限制為Vmax。如果粒子第j維的速度絕對值|vij|＞Vmax,j，則該維速度值被限制為Vmax,j，同時保持速度方向不變。粒子位置的第j維xij也被限制在相應的搜索范圍[Xmin,j,Xmax,j]。如果粒子在運動過程中，其位置超出了邊界，則要進行相應的邊界處理[16]。

標準PSO算法步驟如下：

（1）令t=0，初始化種群中粒子的位置xi(0)與速度vi(0)，設定最大速度Vmax與位置邊界Xmax，Xmin。初始的粒子個體最優(yōu)位置pi=xi(0)。

（2）計算每個粒子的適應值f(xi(t))。

（3）更新每個粒子的個體最優(yōu)位置pi：如果f(xi(t))＜f(pi)，則pi=xi(t)。

（4）更新全體最優(yōu)位置pg：對于所有的i=1,…,Np，如果f(pi)＜ f(pg)，則pg=pi，g=i。

（5）根據(jù)式（1）更新每個粒子的速度。若粒子速度越界，進行越界處理。

（6）根據(jù)式（2）更新每個粒子的位置。若粒子位置越界，進行越界處理。

（7）t=t+1，如滿足結(jié)束條件，算法結(jié)束；否則，轉(zhuǎn)（2）。

判斷終止條件是設置適應值到達一定的數(shù)值或者循環(huán)一定的次數(shù)。

3.2 利用粒子群算法求解多項目系統(tǒng)總收益最大化目標模型

3.2.1 確定模型的變量

在上述多項目系統(tǒng)總收益最大化目標模型中，要優(yōu)化的變量為瓶頸資源在各項目中的分配順序。例如有4個項目，瓶頸資源在這4個項目中分配順序有24種組合。這些組合稱為變量。每種組合x→稱為一個個體/粒子。

3.2.2 確定目標函數(shù)

調(diào)度模型的目標值是最大化項目收益的權重和，它是衡量瓶頸資源調(diào)度方案優(yōu)良情況的標準。在粒子群算法中，粒子的一個位置表示問題的一個解，即資源的一個可行調(diào)度方案，每個粒子性能的優(yōu)劣程度取決于待優(yōu)化問題目標函數(shù)確定的適應值，本文的適應度函數(shù)即目標函數(shù)為

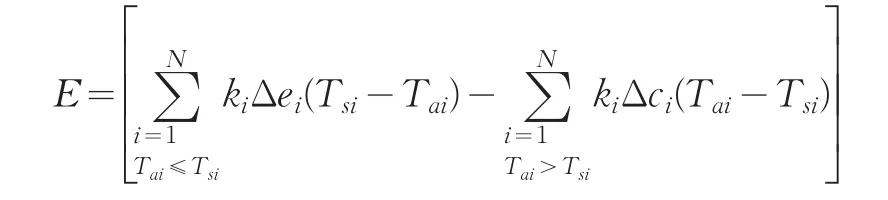
3.2.3 進化方程設計

PSO中并沒有許多需要調(diào)節(jié)的參數(shù)，從現(xiàn)有研究來看，這些參數(shù)的經(jīng)驗設置為

粒子群：一般取20～40；

學習因子：c1和c2通常等于2，不過也有其他的取值，但是一般c1=c2，并且范圍為[0,4]；

中止條件：設定一定的迭代次數(shù)。

3.2.4 收斂條件

收斂性是粒子群算法的一個重要問題，它可以說明這種算法找到的可行解是否最優(yōu)或者當前找到的解是否滿足精度要求。

3.2.5 把實數(shù)解轉(zhuǎn)化為整數(shù)解

粒子群算法所求出的解是實數(shù)形式的，由于本文所討論問題的特殊性，所要優(yōu)化的變量是整數(shù)，而且是一種排序方式，因此在迭代過程中產(chǎn)生的解可能不合法，就要將不合法的實數(shù)解轉(zhuǎn)化為整數(shù)解，并把整數(shù)列轉(zhuǎn)化為排序的形式，每個值必須而且只能出現(xiàn)一次，步驟如下：

（1）將算法得到組合中的每個數(shù)向上取整，比如組合[1,3.4,3.5,2]向上取整后變?yōu)閇1,4,4,2]；

（2）找出重復的數(shù)字。從向上取整后的組合可以看出，組合中有兩個4，為重復的數(shù)字；

（3）保留不重復的數(shù)字，對于重復的數(shù)字保留一個，其他的進行替換，將組合中應該出現(xiàn)而未出現(xiàn)的數(shù)字替換重復的數(shù)字。如向上取整后的組合中，保留1和2，有兩個4而未出現(xiàn)3，應該用數(shù)字3來替換其中的一個4，替換后的結(jié)果為[1,3,4,2]或[1,4,3,2]。

4 算例驗證

假設有8個并行項目共享一個單位的瓶頸資源，項目的參數(shù)見表2

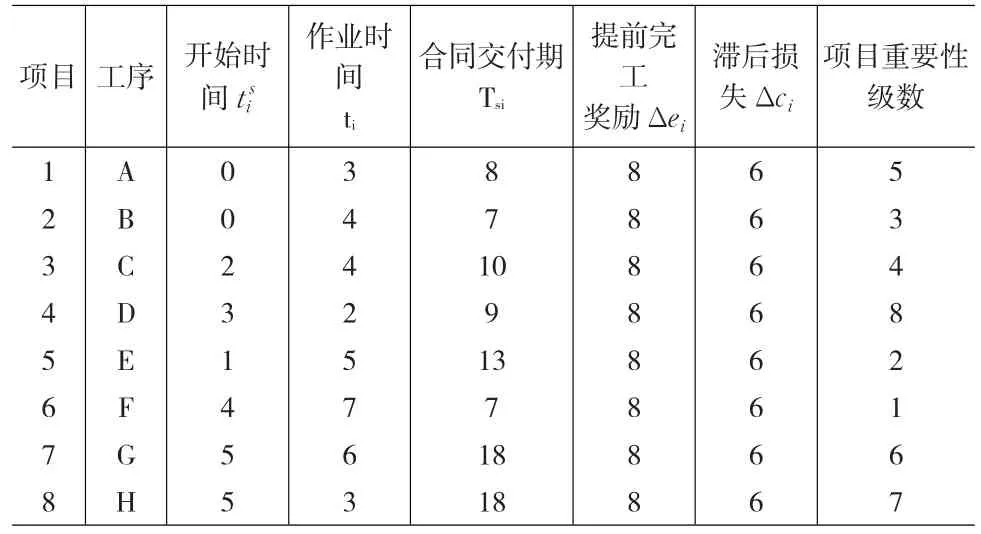
表2 項目參數(shù)

我們采用粒子群算法來解決總收益最大化問題，所采用的粒子群算法參數(shù)如下：最大迭代代數(shù)為100，初始粒子群規(guī)模為30，慣性權w=0.55，加速系數(shù)c1=c2=2，用Matlab編程語言實現(xiàn)，在硬件環(huán)境：CPU：N270 160GHz、內(nèi)存：1.99GB等和軟件環(huán)境WindowsXP系統(tǒng)下運行程序。得到的瓶頸資源分配順序滿意解為[2，4，8，1，3，7，5，6]，對應的總收益E=153。

由于粒子群算法的隨機性（r1j和r2j為在[0,1]內(nèi)均勻分布的隨機數(shù)），每次運行程序所得到的解可能不同，為了檢驗粒子群算法的收斂性，我們運行程序20次，得到一條平均結(jié)果的收斂曲線，見圖1。

從圖1可以看出，在迭代將近40次的時候已經(jīng)接近滿意解，之后的迭代則為精細搜索，得到的解越來越靠近滿意解，這也說明了粒子群算法在解決多項目瓶頸資源分配問題時的有效性。

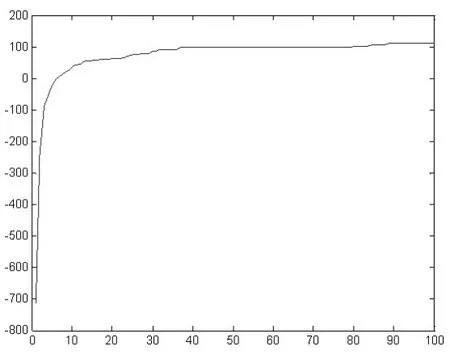
圖1 粒子群算法運行20次得到的收斂圖

5 結(jié)論

本文詳細分析了Goldratt提出的關鍵鏈多項目管理5步驟應用法，從定量的角度，在多項目環(huán)境中對關鍵鏈瓶頸資源約束下考慮多項目總收益最大化目標建立了數(shù)學模型，引入粒子群算法解決瓶頸資源在多項目中的分配順序問題。粒子群算法作為新近出現(xiàn)的一種仿生優(yōu)化算法，具有隨機搜索的優(yōu)點，且不容易落入局部最優(yōu)解，并保證了算法的快速性。本文簡要地描述粒子群算法的基本概念并給出粒子群算法在關鍵鏈多項目進度優(yōu)化模型中的應用流程，通過算例證明了粒子群算法在解決該問題的可行性、實用性和有效性，為關鍵鏈多項目進度優(yōu)化問題提供了一種新的思路和方法。

需要指出的是，本文解決了單模式下關鍵鏈多項目管理中瓶頸資源的分配問題，對于多模式的情況需要進行進一步的討論研究。

[1]Coldratt E M.Critical Chain[M].New York:the North River Press,1997.

[2]Steyn H.Project Management Applications of the Theory of the Con?straints Beyond Critical Chain Scheduling[J].International Journal of Project Management,2002,20(1).

[3]Rabbani M.a,S.M.T.Fatemi Ghomi b,*,F.Jolai a,N.S.Lahiji a.A New Heuristic for Resource-constrained Project Scheduling in Sto?chastic Networks Using Critical Chain Concept[J].European Journal of Operational Research,2007,176.

[4]Herroelen WS,Leus R,Demeulemeester EL.Critical Chain Project Scheduling:do not Over Simplify[J].Project Manage Journal,2002,33(4).

[5]Cohen I.,A Mandelbaum,Et al.Multi-Project Scheduling and Con?trol:A Process-based Comparative Study of the Critical Chain Meth?odology and Some Alternatives[J].Project Management Journal,2004,35(2).

[6]Leach,L.P.Critical Chain Project Management Improves Project Per?formance[J].Project Management Journal,1999,30(2).

[7]Lechler,Thomas G.Boaz Ronen,Edward A.Stohr.Critical Chain:A New Project Management Paradigm or Old wine in New Bottles?[J].Engineering Management Journal,2005,17(4).

[8]楊雪松，胡昊.基于關鍵鏈方法的多項目管理[J].工業(yè)工程與管理，2005,（2）.

[9]郭慶軍，賽云秀.關鍵鏈多項目進度管理分析[J].西安工業(yè)大學學報，2007，27（6）.

[10]馬國豐，屠梅曾，史占中.基于TOC的項目管理技術模型[J].系統(tǒng)工程理論方法應用，2005，14（1）.

[11]馬國豐，尤建新.關鍵鏈項目群進度管理的定量分析[J].系統(tǒng)工程理論與實踐，2007，27（9）.