大型可展收支撐臂模態試驗研究

檀傈錳 白化同 程剛 丁鋒

（北京空間飛行器總體設計部，北京 100094）

1 引言

大型可展收支撐臂具有較高的收藏比，可實現由折疊狀態到展開狀態的轉換，在航天領域得到越來越多的應用。為了防止支撐臂與星上其他系統發生共振，需要掌握其在工程設計要求頻帶范圍內的主要動態特性，包括固有頻率、模態阻尼和模態振型。采用有限元模型（Finite Element Model，FEM）進行模態分析，力學模型簡化不當、邊界處理與實際結構狀態存在差異等因素都對分析結果的準確性造成影響［1］。

2 模態試驗試件介紹

2.1 支撐臂構造

處于展開狀態的支撐臂試件為一格柱式桁架，如圖1所示［3］，由若干數量的構架單元組成。每個單元由球鉸接頭、縱梁、橫向框架、導向輪和斜拉索組件組成，結構桿件材料為碳纖維／環氧樹脂復合材料，拉索材料為鋼，球鉸接頭、導向輪等其余部件材料為不銹鋼。用于試驗的支撐臂試件長約25m，前端配置負載安裝接口。由于縱梁兩端為鉸接、拉索具有一定彈性，使得支撐臂在振動上具有一定的非線性。

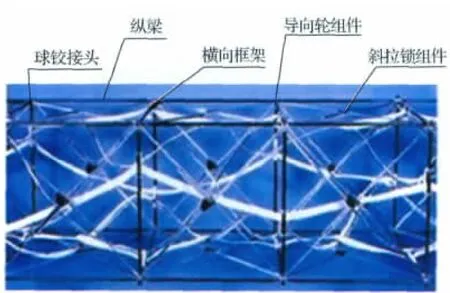
圖1 大型可展收支撐臂示意圖Fig.1 Sketch of large deployable support beam

2.2 支撐臂安裝

支撐臂構架展開時，斜拉索與根部鎖止裝置均鎖定到位。如圖2所示，各構架通過彈簧吊掛裝置與零重力展開試驗架相連，模擬其在軌運行狀態。

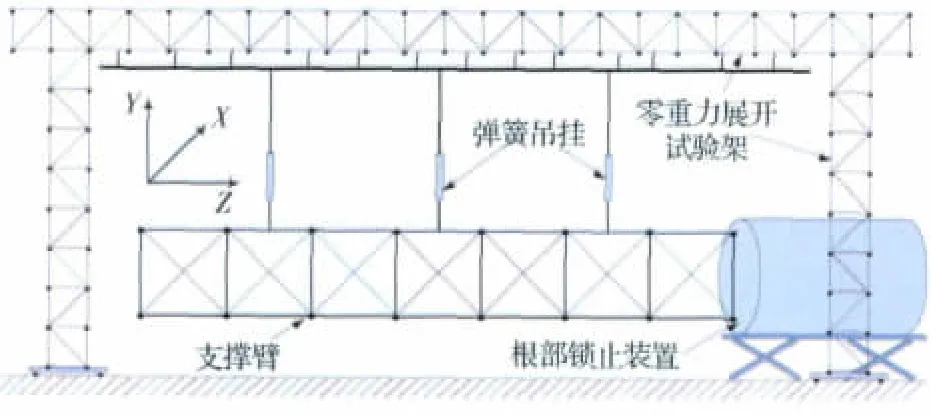
圖2 支撐臂吊掛示意圖Fig.2 Sketch of support beam installation

支撐臂坐標系如圖2所示，沿中心軸的收攏方向定義為Z 向。彈簧吊掛對試件造成了附加剛度、附加質量和附加阻尼效應，它們與支撐臂主體構架還構成了扭擺和單擺效應。因此，模態試驗得到的是支撐臂與彈簧吊掛整個系統在特定邊界條件下的模態參數。

3 模態試驗方案

支撐臂每一框架單元為中心對稱結構。橫向框架為固接，相比于伸展方向，橫向框架面內剛度較高，在振動過程中形狀保持不變。因此，可將伸展臂簡化為Y、Z 面內的一個平面，研究其在X 方向上的移動及繞Z 軸的轉動。對各鉸接位置進行編號，用于傳感器和激振器布置。負載安裝接口為1點，其余位置沿Z 向依次編號。

3.1 響應點數目和位置選取

響應點的數目和位置應以全面表征的各階模態振型為目的，同時避免對結構局部質量和剛度影響過大。根據文獻［4］中的方法和經驗初步選取傳感器安裝位置，在此基礎上，根據有限元模型模態分析結果，采用模態置信準則（Modal Assurance Criterion，MAC）對響應點評價。MAC矩陣表示如下：

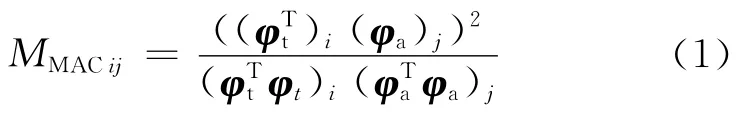
式中：（φt）i、（φa）j分別為第i階、第j階的全模型和試驗模型的模態向量矩陣。以MAC 矩陣非對角元素最小化為目標對響應點數量和位置進行優化，要求MAC 矩陣對角線元素＞0.9，非對角線元素＜0.1。將具有1464個自由度的全模型FEM 簡化為具有21個自由度的試驗模型。圖3（a）為響應點位置優化前后的MAC 矩陣，左側矩陣中的黃色區域表示優化前支撐臂的第一階和第二階振型具有一定的相似性，優化后各階振型區分明顯。圖3（b）為優化完成后的響應點布局（圖中黃色圓點），部分響應點編號如圖3（b）所示。

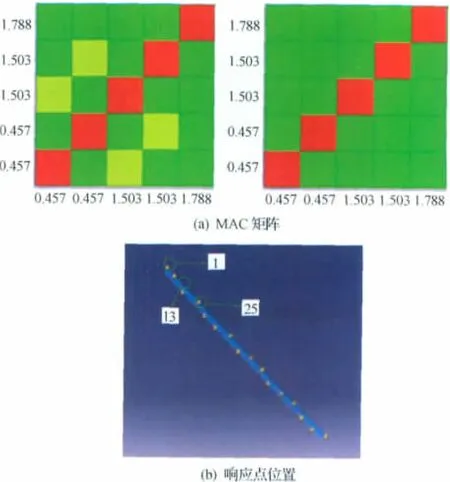
圖3 MAC矩陣及響應點分布Fig.3 MAC matrix and sensor locations

3.2 激勵點位置選取

激勵點的選取首先考慮剛度和平均模態位移較大的點，并保證激振器對結構的耦合影響和激振器間的相互影響盡量小［5］。采用激勵點留數（DrivingPoint Residue，DPR）方法找到最適于試件激勵的位置。如圖4所示，對激勵點留數計算結果排序有最大、最小、平均和加權平均4種方式，以加權平均最小作為選擇依據。

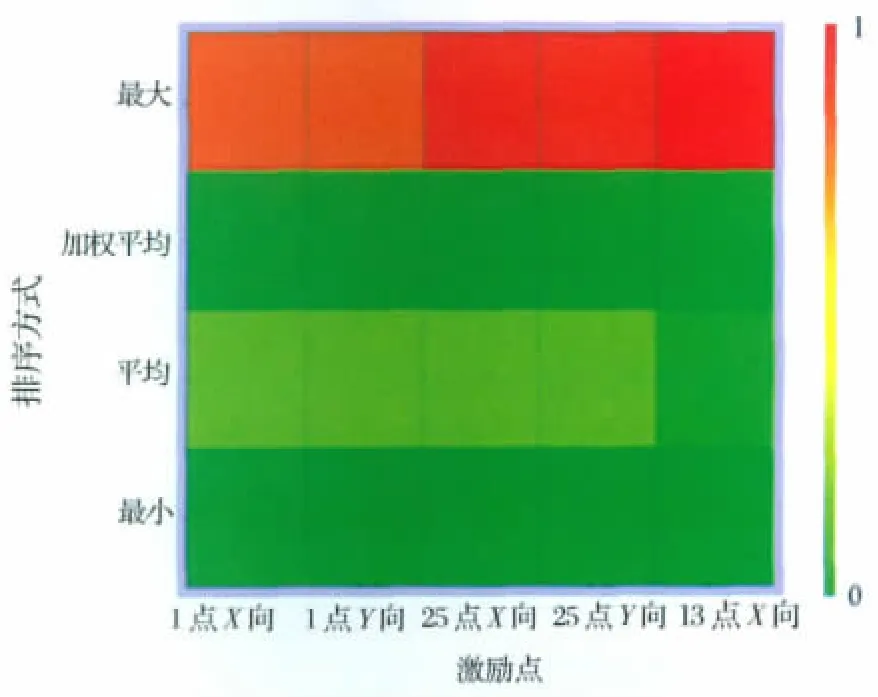
圖4 激勵點留數Fig.4 Exciting point residues

通過計算激勵點留數［6］，得到前5個優選自由度，如圖4所示，最終選擇1點和25點的X 向進行激勵。

煙臺市通過大力實施生態建設工程，不斷加大環境保護力度，加強重點流域濕地建設，推動森林和濕地資源實現穩步增長。今年以來，煙臺市完成造林11.68萬畝，森林撫育20萬畝，濕地保護與修復7.6萬畝，生態環境持續改善。

3.3 激勵方法選擇

多點隨機激勵方式適用于模態辨識，且此種激勵與航天器在軌實際工況比較接近。正弦激勵方法可直接觀測處于共振中的結構特性參數，但該方法耗時較長，適用于頻率范圍已知的情形。在本試驗中，采用多點隨機和單點步進正弦兩種激勵方法，激振力的量級根據不同的試驗方法和實際情況在試驗過程中調整確定。

3.4 模態試驗系統

模態試驗系統組成如圖5所示，系統由激勵子系統、數據采集子系統和模態分析子系統組成，設備主要技術參數見表1。

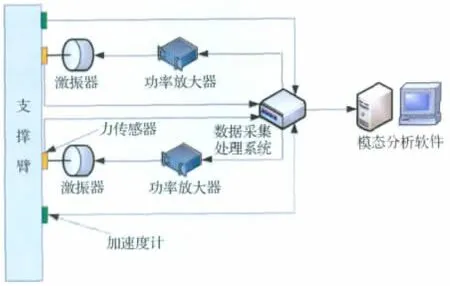
圖5 模態試驗系統示意圖Fig.5 Sketch of test system

激勵子系統包括激振器、功率放大器、力傳感器和數據采集系統的激勵信號發生器組成。2臺激振器用于多入多出（Multiple Input Multiple Output，MIMO）的隨機激勵試驗，1臺激振器用于單點步進正弦試驗，2個力傳感器用于激振力的測量。

數據采集子系統包括加速度計和數據采集處理前端。6個電容式加速度計用于響應測量。數據采集處理前端包含有3塊24位低頻電壓輸入模塊和1塊24位的信號源輸出模塊。

模態試驗的激勵控制、響應測量、數據處理和模態分析，都在LMS Test Lab 11B軟件下完成。

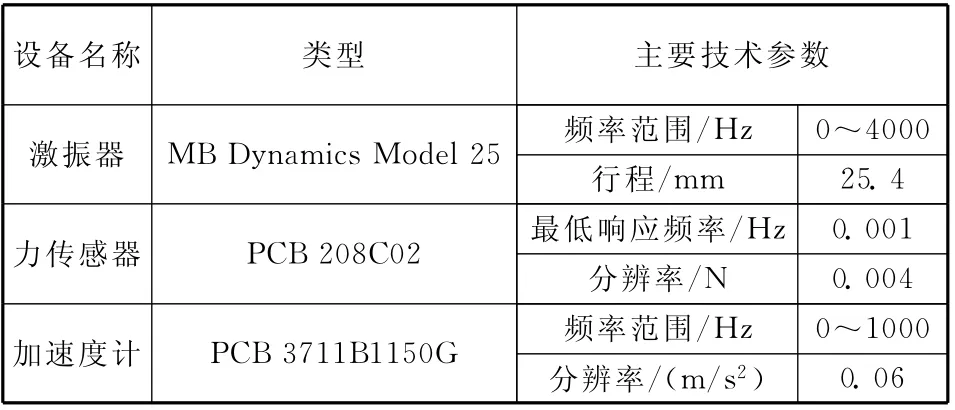
表1 設備技術參數表Table 1 Equipment parameters list

4 試驗實施

在試驗過程中，采用多點隨機激勵和單點步進正弦激勵2種試驗方法。對猝發隨機和平穩隨機2種激勵信號進行了對比，以測試數據具有較好相干性作為評判依據［7-8］。在步進正弦激勵試驗中，為節省試驗時間，在不同頻率范圍內采用不同的掃描速率。由于傳感器數量有限，每次模態試驗分為3部分測試完成。

4.1 隨機激勵方式試驗條件的確定

圖6為采用不同量級激振力量級（0.5V、1V、2V，通過控制輸出電壓實現控制激振力的量級）獲得的頻率響應函數（Frequency Response Function，FRF）曲線和相干函數［6］曲線，激振力較小的情形（圖6中紅色曲線）在1 Hz以下具有一個較高的峰值，而當激振力較大時測量結果的相干性較好。

圖7為采用平穩隨機信號和猝發隨機信號分別進行激勵的相干函數曲線，可見，針對支撐臂這種低頻、振動響應具有非線性的結構，平穩隨機信號比猝發隨機信號更具有適用性。

綜合以上分析，在多點隨機激勵試驗過程中，所選擇的試驗條件參數是：平穩隨機激勵，激振力量級0.5V，頻率帶寬為0～16Hz，分辨率f＝0.015 6Hz。

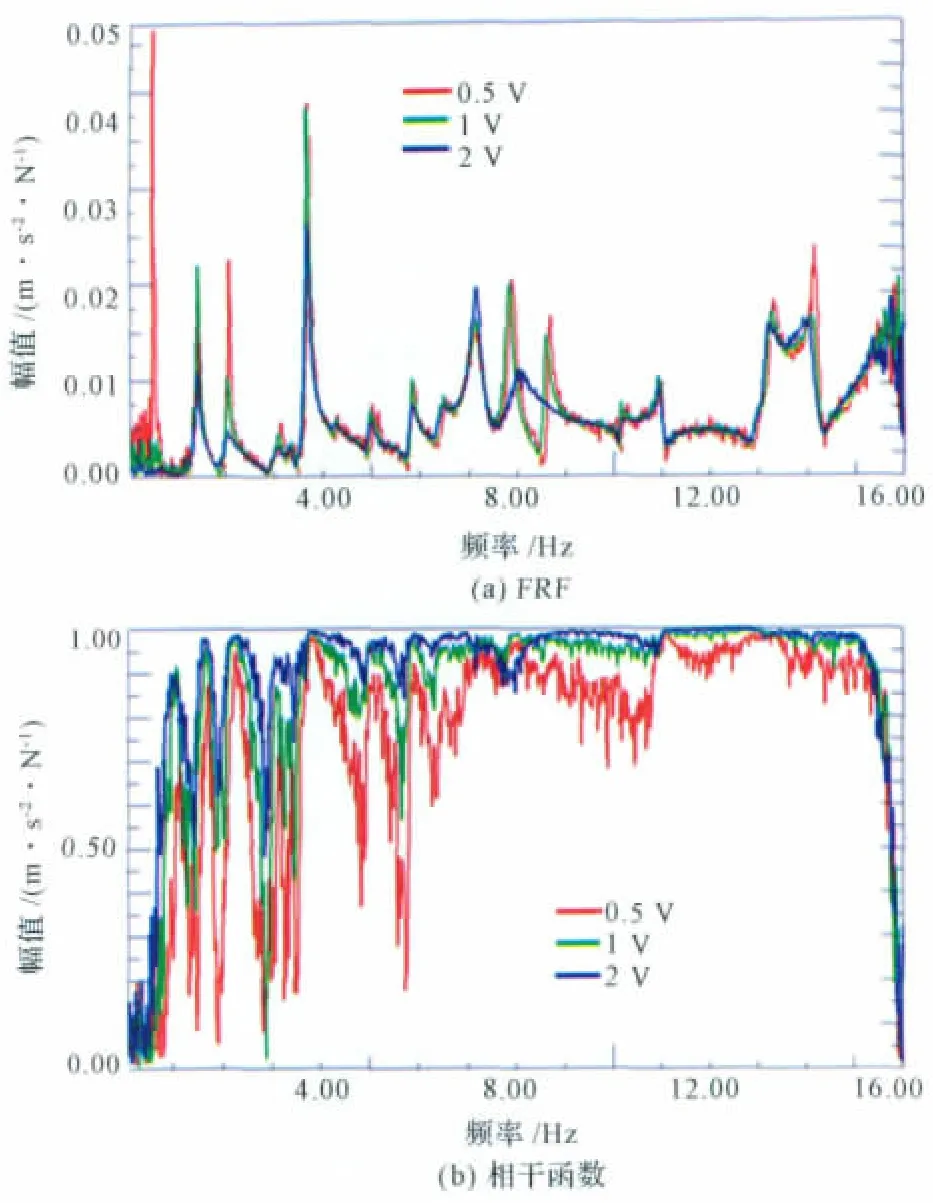
圖6 不同量級激振力的FRF和相干函數對比Fig.6 FRFs and coherence for different excitation level

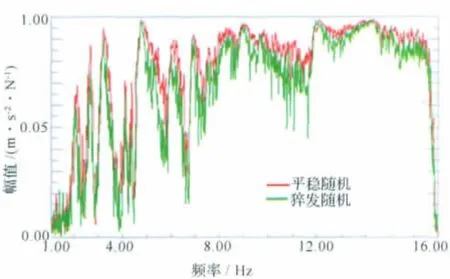
圖7 平穩隨機信號與猝發隨機信號相干函數對比Fig.7 Coherence for stationary random signal and burst random signal

4.2 步進正弦激勵方式試驗條件確定

在步進正弦激勵試驗中，一個重要參數是掃描速率。分別進行了0.001Hz／s和0.005Hz／s兩種不同掃描速率的激勵響應對比，如圖8所示，可見當掃描速率較大時，FRF 曲線（圖8 中藍色曲線）在1.4Hz時的峰值較小，且兩種掃描速率下FRF 曲線峰值頻率有一定的偏差。隨著掃描速率的下降，結構有更多的時間對輸入作出響應，所以，峰值頻率更接近所關心模態的實際穩態峰值頻率。

圖9為激振力信號的自功率譜密度，在低于0.5Hz時信號的能量級非常小，對準確獲得該頻段內的模態頻率造成較大影響。

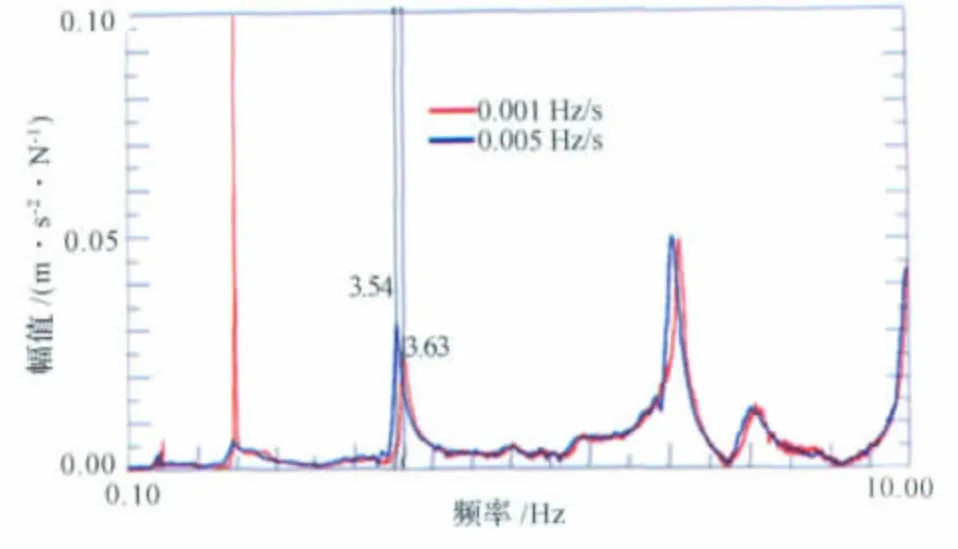
圖8 不同步進速率下的FRF曲線Fig.8 FRF at various step rates

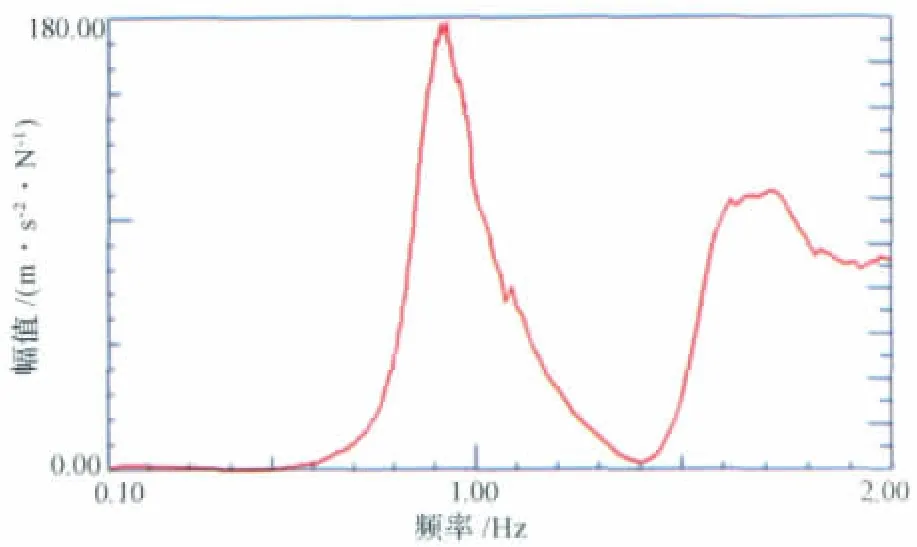
圖9 激勵信號的功率譜Fig.9 Power spectrum of exciting signal

本文主要獲取支撐臂的低頻響應特性，為節省試驗時間，所選試驗條件為：掃描頻率帶寬為0.1～10Hz，在0.1～1 Hz范圍內掃描速率0.001 Hz／s，1～10Hz范圍內掃描速率0.01Hz／s。

5 試驗結果分析及驗證

5.1 試驗結果分析

圖10為支撐臂模態試驗的穩態圖，由于結構振動響應非線性較大，在圖10（a）上有多個虛假模態，需要根據工程經驗和模態振型將虛假模態剔除掉。通過圖10（b）可以看出，由于力傳感器、加速度計在0.5Hz左右的低頻響應相對較差，穩態圖內低頻段峰值相對不明顯。

圖11為支撐臂模態試驗得到的前6階模態振型，可看出各階模態振型較為清晰，獲得了較為準確的試驗結果。

表2為采用單點步進正弦和多點隨機2種激勵方法分別獲得的支撐臂系統模態參數，在高頻部分（2Hz以上）2種激勵方法得到的固有頻率相差在5%以內，而低頻部分2種激勵方法得到的固有頻率相差7.20%，并且采用平穩隨機激勵方法沒有得到支撐臂的第一階彎曲振型。由圖7可以看出，平穩隨機激勵方法獲得的響應信號相干性較差，此方法在研究支撐臂此類低頻、振動響應具有非線性結構的模態特性上適用性較差。

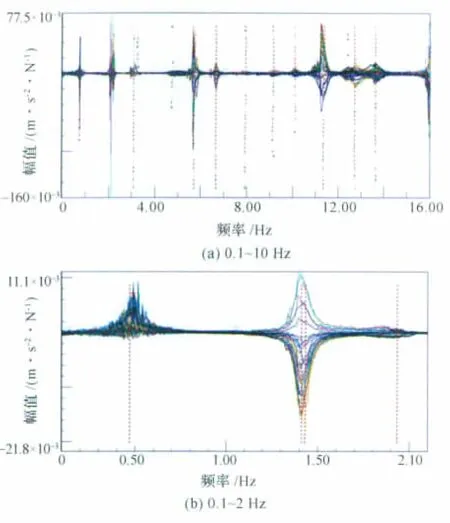
圖10 模態試驗穩態圖Fig.10 Stabilization diagram of modal test

圖11 支撐臂模態振型示意圖Fig.11 Mode shapes of support beam

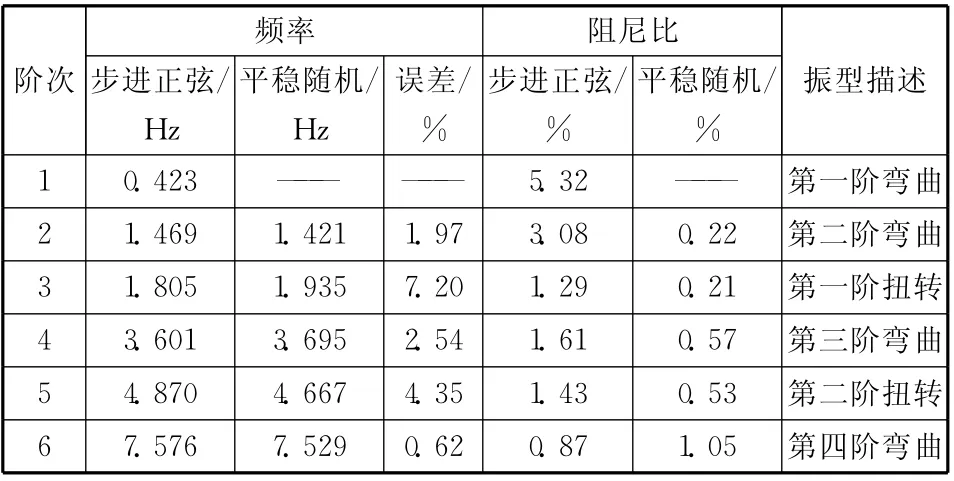
表2 不同激勵方法下支撐臂模態參數對比Table 2 Comparison of modal parameter for different excitation method

表3中將支撐臂模態試驗結果與FEM 分析結果進行了對比，FEM 分析沒有得到第二階扭轉模態，具體原因需要進一步分析研究。試驗結果與FEM 分析結果在第二階以后相差較小，但第一階固有頻率相差7.44%，相對較大，同時根據試驗結果發現，支撐臂系統第一階彎曲模態的阻尼比較大，達到了5.32%（見表2），針對此種情況需做進一步分析。

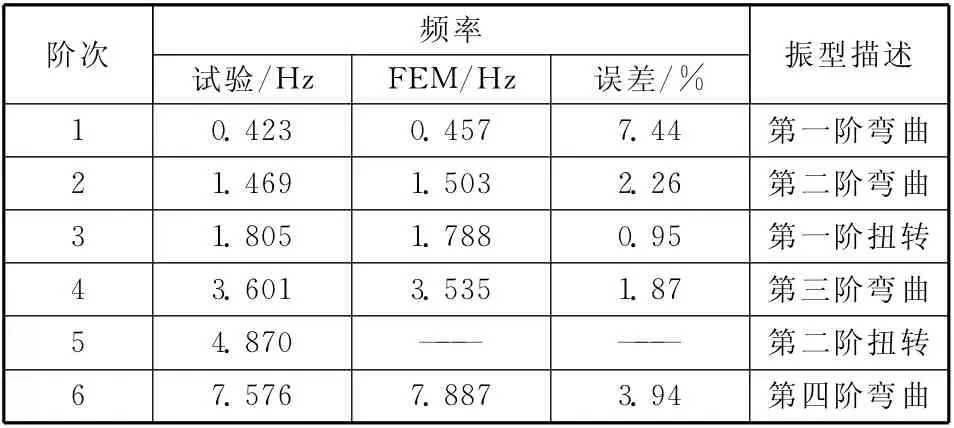
表3 試驗結果與FEM 分析結果比較Table 3 Comparison of test result and FEM analysis result

5.2 模態驗證

表4為根據試驗模態數據建立的MAC 值矩陣，非對角線元素值相對較小，模態辨識理想，試驗結果可靠。

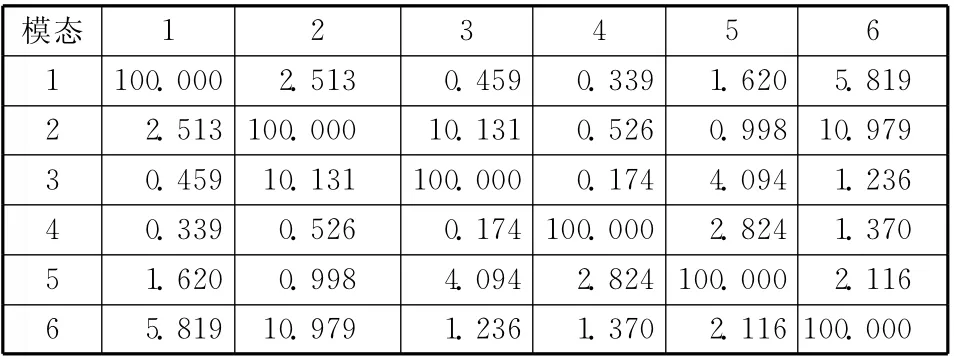
表4 支撐臂模態MAC矩陣Table 4 MAC matrix for support beam modal test

6 結束語

本文針對大型可展收支撐臂開展了模態試驗研究，結合有限元方法對試驗結果進行了分析，試驗結果較好地反映了支撐臂的動力學特性。對于低頻、振動響應非線性的伸展機構的模態試驗，多點隨機激勵法在辨識低頻部分模態時適用性較差。為獲取系統的低頻模態參數，可采用步進正弦激勵方法。采用有限元方法確定激勵點位置和響應點數量及位置，可實現采用盡量少的傳感器充分捕獲系統各階模態參數的效果。本文的研究內容對于開展太陽翼、展開天線等具有低頻、大撓度、振動響應非線性特點的大型部件的模態試驗具有一定的借鑒意義。

（References）

［1］周志成，曲廣吉.星載大型網狀天線非線性結構系統有限元分析［J］.航天器工程，2008，17（6）：33-38 Zhou Zhicheng，Qu Guangji.Nonlinear finite element analysis of large mesh deployable antenna on satellite［J］.Spacecraft Engineering，2008，17（6）：33-38（in Chinese）

［2］吳素春，賈文成，邱吉寶.載人運載火箭全箭模態試驗［J］.宇航學報，2005，26（5）：531-534 Wu Suchun，Jia Wencheng，Qiu Jibao.Integrated modal test for the manned launch vehicle［J］.Journal of Astornautics，2005，26（5）：531-534（in Chinese）

［3］程剛，丁鋒，柴洪友，等.基于空間干涉遙測的大型可展收支撐結構研究［J］.機械設計與制造，2009，5：145-146 Cheng Gang，Ding Feng，Chai Hongyou，et al.Re-search on the large deployable support beam based on space remote interferometry［J］.Machinery Design ＆Manufacture，2009，5：145-146（in Chinese）

［4］Kammer D C.Sensorplacement for on-orbit modal identification and correlation of large space structures［J］.Journal of Guidance，1991，14（2）：2984-2990

［5］Larson C B，Zimmerman D C，Marke E L.A comparison of modal test planning techniques：excitation and sensor placement using the NASA 8-bay truss［C］／／Proceedings of 12th International Modal Analysis Conference.Washington：NASA，1994

［6］沃德·海倫，斯蒂芬·拉門茲.模態分析理論與試驗［M］.白化同，郭繼忠，譯 .北京：北京理工大學出版社，2001 Ward Heylen，Stefan Lammens.Modal analysis theory and testing［M］.Bai Huatong，Guo Jizhong，translated.Beijing：Beijing Institute of Technology Press，2001（in Chinese）

［7］Gaspar J L .Development of modal test techniques for validation of a solar sail design［C］／／45th AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics ＆ Materials Conference.Washington：AIAA，2004

［8］Buehrle R D，Templeton J D，Reaves M C，et al.Ares I-X flight test vehicle：stack 5modal test，NASA／TM-2010-216183［R］.Washington：NASA，2010