子帶OFDMA中EM雙選信道估計的收斂性能分析

陳東華

（華僑大學信息科學與工程學院，福建廈門361021）

子帶OFDMA中EM雙選信道估計的收斂性能分析

陳東華

（華僑大學信息科學與工程學院，福建廈門361021）

算法實時性是通信系統可實用化的關鍵，為了揭示子帶正交頻分多址(OFDMA)系統中期望最大化(EM)雙選信道估計的實時性，研究了子帶OFDMA系統中EM算法的收斂性能.通過系統仿真方法分別給出了單天線系統和多天線系統EM迭代信道估計的收斂曲線，研究結果表明，兩種迭代信道估計都有較快的收斂速度，而且多天線系統比單天線系統收斂更快，前者僅需3次迭代即可收斂，而后者在10次迭代內也可保證收斂.理論分析顯示，迭代過程中參數更新數目的不同是導致兩種算法收斂性能不同的原因所在.

正交頻分多址；收斂速度；信道估計

0 引言

正交頻分復用（OFDM）利用子載波間正交性提高了頻譜利用效率，是一種頻譜有效的傳輸技術[1]，經過多年的研究，學術界和產業界已經把OFDM作為多種移動通信標準的物理層傳輸方案[2]，如無線局域網標準IEEE802.11a和下一代移動通信（4G）都采用了該技術[3].同時，OFDM特有的頻分復用方式使得該技術很容易實現多址接入，子帶正交頻分多址(OFDMA)即是一種常用的多址接入方式.

通信系統中為了相干解調，接收機通常采用導頻進行信道估計.子帶OFDMA系統的導頻信道估計方法中，通常把導頻信號分散在時間頻率的二維網格上，并通過時間和頻率方向的線性插值得到數據子載波上的信道頻域響應.然而在高速移動環境中，傳輸信號將同時遭受時間和頻率選擇性衰落（雙選擇性衰落）[4].隨著移動臺移動速度的加快，這種情況下的信道變化將不再滿足線性規律，導致線性插值的導頻信道估計性能的嚴重惡化，為了解決這一問題，文獻[5]提出了采用頻域線性模型和時域基擴展模型(BEM)混合插值(HLBI)的子帶OFDMA導頻信道估計方法，該方法在時間方向上利用基擴展模型插值代替常規線性插值，從而改善了信道時變導致的OFDMA系統性能惡化，但是該方法在頻率格上依然采用常規方法，即線性內插，當信道頻率選擇性較為嚴重時，文獻[5]方法的性能改進受到信道頻率選擇性的制約.

為了克服文獻[5]方法的缺點，文獻[6]對信道響應在頻率方向的變化不做任何假定，而對接收信號做形式變換并在此基礎上定義信道的頻域BEM模型，進而提出了兩種基于期望最大化（EM）算法的子帶OFDMA信道估計新方法，從而避免了文獻[5]信道估計方法的缺點.文獻[6]對信道估計的均方誤差和誤碼率性能進行了詳細分析，但并未考慮算法的收斂問題.EM迭代算法的收斂性能是系統可實時性的關鍵，文中在介紹文獻[6]兩種EM信道估計的基礎上仿真研究了算法的收斂性能，并結合理論分析探討了產生兩種算法收斂性能不同的內在機理.

1 信道估計模型

1.1 單發射天線EM信道估計

采用過采樣復指數BEM[7-8]對N個連續傳輸塊上的時變信道進行建模，第l條路徑的時變信道脈沖響應(CIR)的可寫為：

其中rq，l定義為第l個抽頭的第q個BEM基系數，L、2Q+1和P分別定義為最大路徑延時、基擴展個數及采樣倍數.定義M為OFDMA傳輸塊的長度（子載波數），進一步定義K為子帶中包含的子載波數，對式（1）進行M點快速傅里葉變換（FFT）得到所考慮子帶上的信道頻域響應(CFR)：

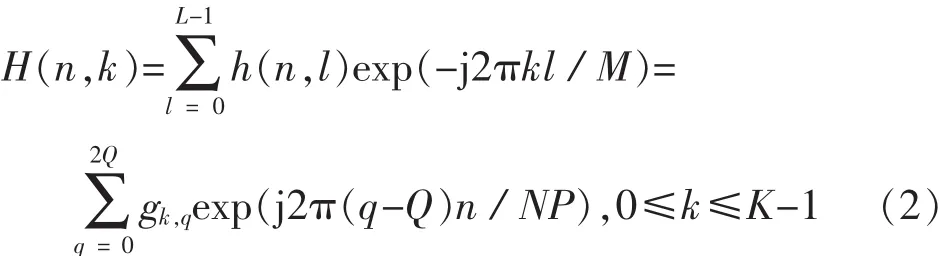
由于式（2）表達的是信道的頻域響應，對比式（1），我們將gk，q定義為頻域等效BEM系數：

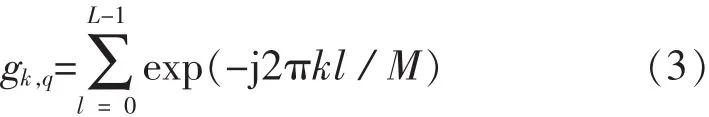
定義X（n，k）為第n個傳輸塊上第k個子載波數據，由文獻[6]，頻域接收信號可寫為Y（n，k）=H（n，k）X（n，k）+W（n，k），其中W（n，k）是對應子載波上的頻域疊加噪聲，W（n，k）服從高斯分布且均值為零、方差為σ2.定義接收矢量Yk=[Y（0，k），…，Y（N-1，k）]T，則接收矢量可表達為Yk=D（Xk）Hk+Wk，其中Xk，Hk的定義形式同Yk，D（·）為對角陣操作符.利用式（2），可將Hk表示成Hk=Qgk，其中gk=[gk，0，…，gk，2Q]T，Q是N×（2Q+1）的基矩陣，其第（m，n）個元素為exp（j2π（m-1）（-Q+n-1））/NP）.把Hk=Qgk代入Yk，可把接收矢量Yk進一步表達成如下形式：

其中Qq定義為Q矩陣的第q列列矢量.為了利用期望最大化算法估計信道參數，定義Yk為“缺損”數據矢量，定義Yk，q=D（Xk）Qqgk,q+Wk，q（q=0,1,…,2Q）為“完備”數據矢量，式中分量Wk，q（q=0,1,…,2Q）定義為矢量Wk的任意分解成分.由定義的缺損數據和完備數據，在式（4）的基礎上可以構造信道參數的EM估計算法.

1.2 多發射天線EM信道估計

KL-BEM是基于時變信道的二階統計量的基擴展模型，其不同基函數之間互相正交[9-10]，可以利用KL-BEM的正交性質來降低計算復雜度.假設多發射天線系統裝備NT個天線，接收系統裝備單個接收天線，則第t個發射天線與接收天線之間的第l條路徑時變信道脈沖響應可表示為：

式中G和rq，t，l分別表示基函數個數和第q個基系數，fq，t，l（n）是n時刻的相應基函數.對于獨立同分布的時頻雙選擇性信道，任意收發天線對之間的L條路徑都具有相同的基函數，因而為了簡化表示，基函數fq，t，l（n）的下標t和l均可以忽略.忽略基函數的下標并對式（5）進行M點離散傅里葉變換可得相應的信道頻域響應為：

同1.1節，gk，q，t定義為頻域基函數系數：

和1.1節的推導過程相同，可以得到N個傳輸塊的第k個子載波上的接收矢量為：

式中Xk，t定義為第t個發射天線的發射數據矢量，gk，t=[gk，0，t，…，gk，G-1，t]T定義為頻域等效基函數系數矢量，F是N×G的基函數矩陣，其第（m，n）個元素為fn-1（m-1）.定義Yk為“缺損”數據，對應的“完備”數據定義為Yk，t=D（Xk，t）Fgk，t＋Wk，t，其中Wk，t為噪聲矢量Wk的NT個任意分解分量之一.由定義的缺損數據和完備數據，根據式（8）不難構造多天線情況下的EM迭代信道估計算法.

2 收斂性能仿真分析

收斂速度是EM迭代算法可實時性的關鍵，借助于系統仿真方法對兩種EM迭代信道估計的收斂性能進行研究.單發射天線系統的仿真參數設定如下：符號長度M=128，子帶長度K=18，信道路徑數L=4；OFDMA傳輸塊數N=61，信道變化快慢用時變信道引起的多普勒頻率對塊長的歸一化[11]來表征，仿真中歸一化多普勒頻率fd取為0.025，此時基擴展的基函數個數取7，導頻等間隔插入且間隔為10，系統初始化方法采用判決輔助跟蹤方式.

為了直觀顯示系統的收斂情況，我們仿真了信道均方誤差(MSE)性能隨著迭代次數變化的關系曲線，見圖1.由圖1不難發現，在兩種信噪比(SNR)條件下，信道MSE均隨著迭代次數的增加而逐漸減小，而且隨著迭代次數的增加MSE的減小量也逐漸減小，例如當迭代次數從0次(相當于無迭代)變化到10次時，15 dB與25 dB兩種信噪比條件下的信道均方誤差分別從0.22和0.21遞減至1×10-2與2.85×10-3，而當迭代次數從10次變化至20次時，兩種條件下的信道均方誤差分別從1×10-2和2.85×10-3僅遞減至9×10-3和1.8×10-3，因而對實際系統應用而言，最大迭代次數只需取到10次.

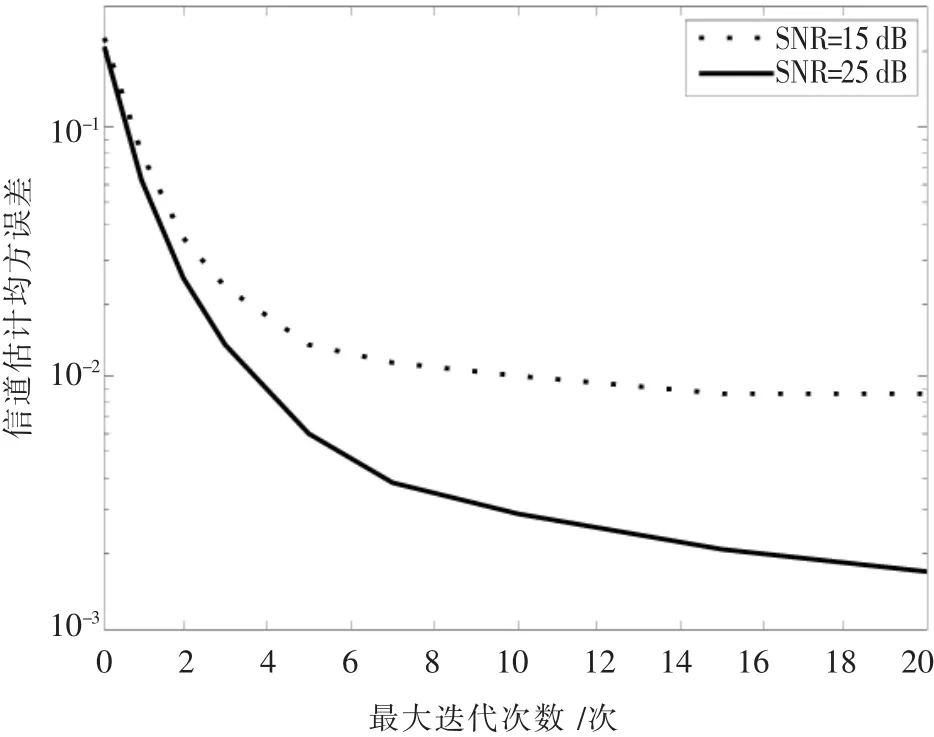
圖1 單天線情況下的收斂曲線

多發射天線系統的仿真參數設定為：系統采用Alamouti編碼來獲得發射分集增益[12]，BEM窗口長度N=102，歸一化多普勒頻率同單天線系統相同，BEM基函數個數取為8，相當于在子帶的兩側等間隔插入22個導頻子載波，并且均勻分散在11個空時碼字的位置上，算法初始化同樣采用判決輔助跟蹤方式.

采用與單天線系統相同的分析思路，我們給出了兩種信噪比條件下信道均方誤差性能隨著迭代次數變化的關系曲線，見圖2.同單發射天線系統相同，信道均方誤差隨著迭代次數的增加而逐漸遞減，例如，當迭代次數從0次增加到3次時，兩種信噪比情況下的信道均方誤差分別從0.20與0.19遞減至3.6×10-3與7.6×10-4，而當繼續提高迭代次數時，信道均方誤差基本不再變化.因而發射分集情況下的收斂速度更快，最大迭代次數只要取到3次便可收斂.

圖2 多天線情況下的收斂曲線

為了進一步證實上面的分析，我們重新給出理想信道和EM迭代信道估計下的系統誤碼率（BER）隨信噪比（SNR）變化的性能曲線，如圖3,4所示.由系統誤碼率曲線可見，無論是在單天線系統還是在多天線系統，EM信道估計條件下的誤碼率都十分接近理想信道下的誤碼率性能，例如，在所考慮的SNR范圍（0～20 dB）內，相對于理想信道條件下的誤碼率性能，單天線信道估計誤碼性能僅有大約3 dB的信噪比損失，而多天線信道估計的誤碼性能損失保持在2 dB信噪比范圍以內.

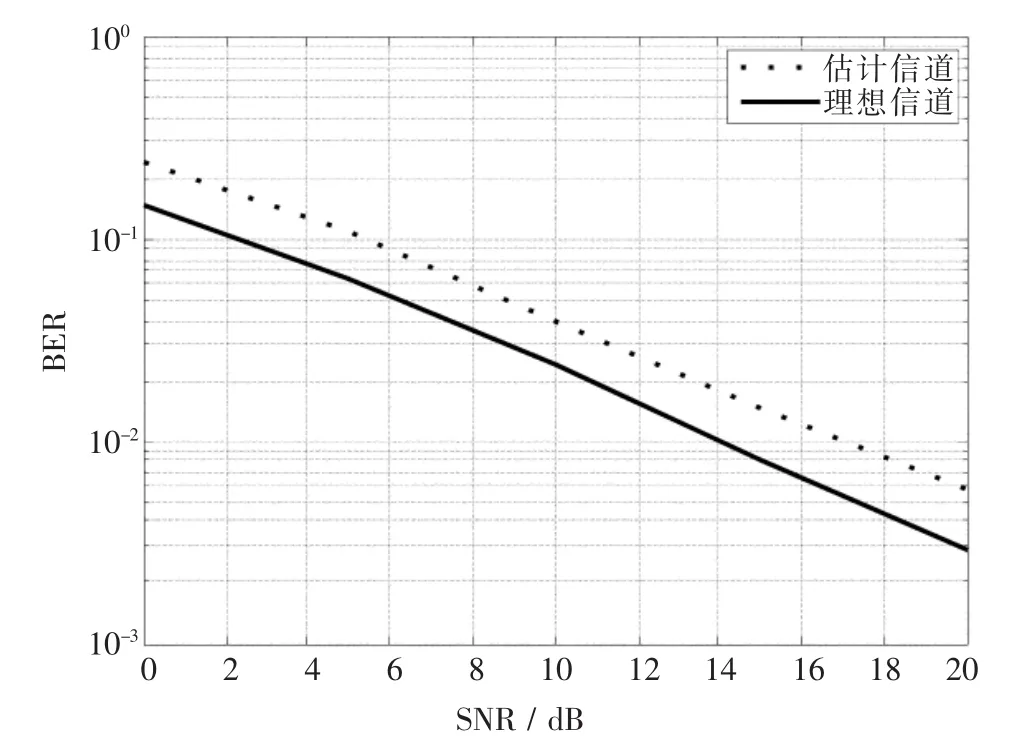
圖3 單天線情況下的誤比特率性能

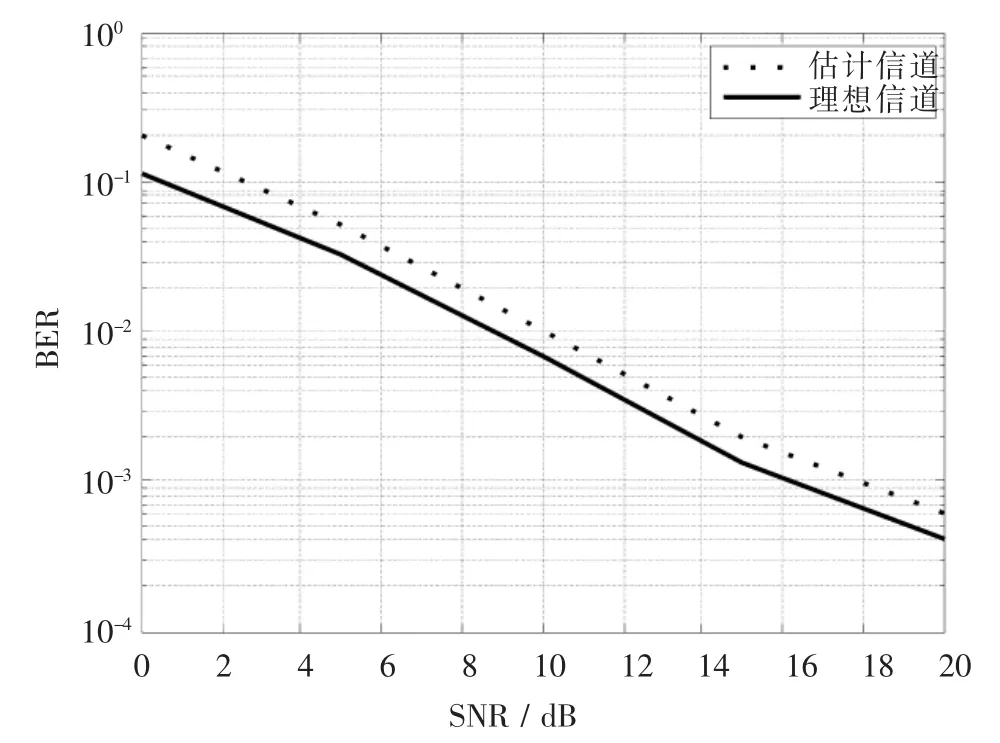
圖4 多天線情況下的誤比特率性能

3 收斂性能理論分析

影響EM算法收斂性能的因素較多，如初始值的精度以及迭代方式的不同都會影響算法收斂性能.如前所述，為了提高初始化精度，兩種EM信道估計均由時頻格兩側的導頻開始，采用判決輔助跟蹤方式初始化算法，因此初始值對兩種算法的影響是完全相同的.除了初值精度，迭代方式本身是影響算法的收斂快慢的重要因素.EM算法由期望（Expectation）和最大化（Maximization）兩步組成，其中最大化是對所有未知變量或矢量同時進行的[13]，這相當于在未知變量或矢量組成的多維空間中進行多維搜索，未知變量/矢量的個數越多，搜索速度越慢，因此EM算法的收斂速度與同時更新的變量或矢量的維數成反比關系.具體到所考慮的兩種EM迭代信道估計，其參數迭代更新過程分別為：

1）單天線系統

期望：

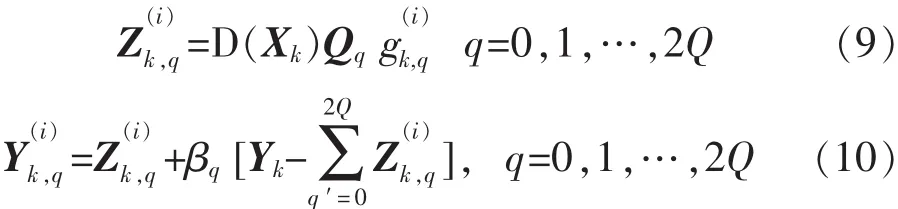
最大：

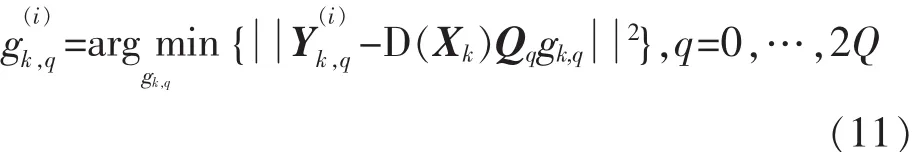
其中i表示迭代順序號，βq非負并且滿

2）多天線系統

期望：

同樣，βt非負并且滿足

最大：

由式（11）和式（14）可見，單天線系統中每次迭代的更新參數為gk，t（q=0，…，2Q），多天線系統中每次迭代的對象是矢量gk，t（t=1，…，NT），即單天線系統是對2Q+1個變量gk，t（q=0，…，2Q）同時進行最大化，而多天線系統中則對NT個矢量gk，t（t=1，…，NT）同時進行最大化.為了系統的物理可實現性，多天線系統的天線數通常為2～4；另一方面，為了信道建模的精度，BEM觀察窗時段對應的基個數應充分大，因此有2Q+1≥NT，具體到文中參數，2Q+1=7，而NT=2，所以單天線迭代算法的收斂速度要慢于多天線迭代算法.同時，仿真結果顯示了兩種迭代算法都具有較快的收斂速度，前者經過大約10次迭代即能收斂，而后者只需3次迭代便可收斂.

通過第二節仿真分析，我們證實了子帶OFDMA系統中采用EM信道估計的可實時性，從而證明了該算法的實用性；而本節對兩種算法參數迭代更新的理論分析顯示，多天線系統每次迭代更新的參數矢量少于單天線系統，這一現象解釋了產生兩種算法收斂速率不同的機理.

4 結束語

子帶OFDMA中的EM信道估計有效提高了時頻雙選擇性信道估計的性能，但在信道估計中每一次EM迭代都需要重新計算信道響應，這會增加系統的計算復雜度并進而影響系統的實時性，迭代次數越多則系統實時性越差，因此EM算法的收斂速度是系統可實時實現的關鍵.文中通過系統仿真手段和理論分析方法分別研究了單天線和多天線系統中EM信道估計的收斂性能，在介紹了這兩種EM迭代信道估計的基礎上給出了算法的收斂性能曲線.仿真結果顯示這兩種迭代信道估計都有較快的收斂速度，研究結果證實了子帶OFDMA中EM信道估計的可實時性，同時通過理論分析方法闡釋了影響EM迭代信道估計收斂快慢的內在因素.

[1]梁小朋，鄧茜，周勇鋒，等.基于訓練序列的定時同步算法研究[J].江西理工大學學報，2011，32(5):46-48.

[2]朱顏銳，田斌，安金坤，等.一種快速OFDM調制信號識別算法[J].西安電子科技大學學報，2012，39(1):17-22.

[3]吳軍，鐘東波.OFDM基帶系統接收器中高性能Viterbi譯碼器的FPGA實現[J].江西理工大學學報，2011，32(3):61-64.

[4]Gupta P，Mehra D K.A novel technique for channel estimation and equalization for high mobility OFDM systems[J].Wireless Pers Commun,2009,49(4):613-631.

[5]Ma Y,Tafazolli R.Channel estimation for OFDMA uplink:a hybrid of linear and BEM interpolation approach[J].IEEE Trans Signal Process,2007,55(4):1568-1573.

[6]Chen D H,Qiu H B.Doubly selective channel estimation for subband OFDMA using basis expansion models[J].Sci China Inf Sci,2011,54(10):2113-2123.

[7]劉英男，蔣偉，姚春光.基于分數倍基擴展模型的雙選信道估計方法[J].北京大學學報：自然科學版，2008，44(1):87-92.

[8]Hou W,Ye W,Feng S,et al.Iterative channel estimation and successiveICIcancellationforOFDMsystemsoverdoubly selective channels[J].Wireless Pers Commun,2009,55:289-303.

[9]Qin W,Peng Q C.Joint channel and phase noise estimation in OFDM using KL expansion[J].International Journal of Electronics and Communications,2008,62(10):777-781.

[10]TeoKAD,OhnoS.OptimalMMSEfiniteparametermodelfordoublyselective channels[C].Proc.of the IEEE Global Telecommunications Conference,2005:3503-3507.

[11]Fang K,Rugini L,Leus G.Low-complexity block turbo equalization for OFDM systems in time-varying channels[J].IEEE Transactions on Signal Processing,2008,56(11):5555-5556.

[12]王雷冬,仇洪冰.Alamouti空時碼在短波信道下的性能分析[J].桂林電子科技大學學報,2011，31(5):361-364.

[13]Pun M-O,Morelli M,Kuo C-C J.Iterative detection and frequency synchronization for OFDMA uplink transmissions[J].IEEE Trans Wireless Commun,2007,6(2):629-639.

Convergence analysis of EM-based doubly selective channel estimation methods for subband OFDMA

CHEN Dong-hua

(College of Information Science and Engineering,Huaqiao University,Xiamen 361021,China)

Real-time computation of an algorithm in communications system is the key for the system to be applicable.In order to reveal whether the channel estimations based on expectation maximization(EM)algorithm in subband OFDMA systems can be on line realized or not,the convergence performance of the EM-based doubly selective channel estimation methods for subband OFDMA is investigated in the article.First,the convergence curves of the two iterative estimators,respectively,for the single transmit antenna system and the multiple transmit antennas system are stated.Results obtained from the convergence curves show that both estimators converge fast,and moreover,the latter does faster with only 3 iterations than the former with a little bigger number of about 10 iterations.Theoretical analysis indicates that the differences in the updated parameter number in iterations account for the two estimators＇differences in convergence speed.

orthogonal frequency division multiple access;convergence speed;channel estimation

TN911.5

A

2012-07-09

中央高校基本科研業務費專項資金資助(11QZR02)；福建省自然科學基金項目資助(2012J05119)；廣西無線寬帶通信與信號處理重點實驗室2011年度主任基金項目(21104)

陳東華（1977-），男，講師，主要從事無線通信等方面的研究，E-mail：dhchen0@163.com.

2095-3046（2012）03-0069-05