異方差回歸模型的經驗似然擬合優度檢驗

唐明田，王允艷

(江西理工大學理學院，江西贛州341000)

異方差回歸模型的經驗似然擬合優度檢驗

唐明田，王允艷

(江西理工大學理學院，江西贛州341000)

由于條件方差函數常常被用來建模和解釋統計數據的多變性，文中考慮了異方差回歸模型中的條件方差函數，構造了一個非參數檢驗程序來檢驗條件方差函數是否為參數形式.因為經驗似然方法具有兩個非常吸引人的性質，一個是該方法的學生化能力使得其能夠自動考慮非參數擬合的變化，另一個是由該方法得到的檢驗統計量的漸近分布與未知參數無關，避免了二次嵌入估計，因此在檢驗過程中文中使用經驗似然檢驗技術來構造擬合優度檢驗的程序，得到了經驗似然檢驗統計量的漸近零分布.

條件異方差函數；經驗似然；擬合優度；Nadaraya-Watson估計量

1 條件異方差回歸模型及假設檢驗

設{（Yi，Xi）}為嚴平穩過程,令m（x）=E（Y=x）和σ2（x）=Var（Y=x）分別為條件均值函數和條件方差函數.文中考慮如下的非參數異方差回歸模型：

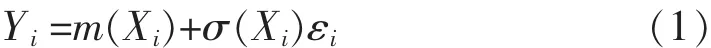
文中將利用經驗似然方法來建立檢驗程序,經驗似然方法是一種計算機密集型的非參數方法,與自助法(bootstrap)相比,經驗似然方法有類似于自助法的抽樣特性,但是相比之下也有其自身的優越性,如所構造的置信區間的形狀由數據自行決定、域保持性、變換不變性等.正因為擁有這些優點,經驗似然方法自提出后已被應用到統計的諸多領域.文獻[9]給出了該方法的詳細的全面的介紹.經驗似然已被證明和參數似然具有某些相同的性質,例如,Wilks＇定理和Bartlett的可修正性原則,詳細介紹讀者可參考文獻[10].正是因為經驗似然方法的諸多優點,使得其在很多領域都得到了廣泛的應用并且被不斷改進.

文中的目的是檢驗條件方差函數σ2（x）是否是參數形式,即考慮如下的原假設:

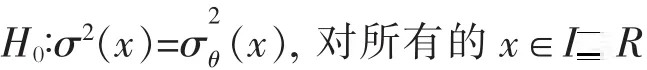
和備擇假設:

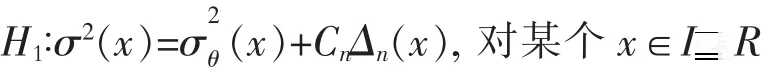
其中,θ∈Θ為未知參數,Cn為當n→∞時趨向于零的非負序列,Δn（x）為有界函數序列.令f（x）為X的密度函數,對某個β〉0，I={x∈R（x）≥β}為緊集.為了不失一般性,文中假設I=[0，1].

2 經驗似然檢驗統計量

文中的檢驗統計量建立在如下的條件方差函數σ2（x）的非參數估計量上:

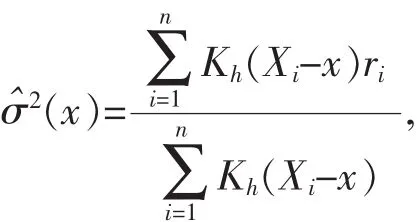
其中,Kh（·）=K（·/h）/h，K（·）為核函數,h 為帶寬,并且

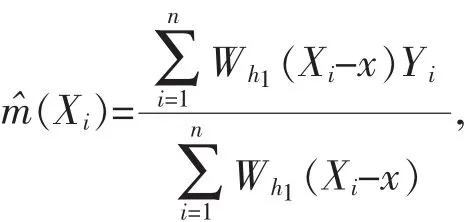
其中,Wh1（·）=W（·/h1）/h1，W（·）為核函數，h1為帶寬.以下設?為θ在原假設下的相合估計量,并令：

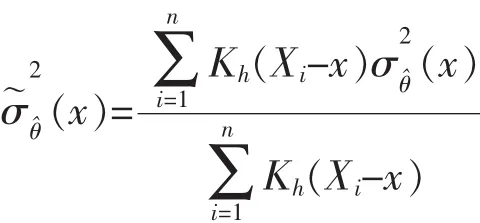
為條件方差函數σ2（x）的參數估計量（x）的核平滑形式.

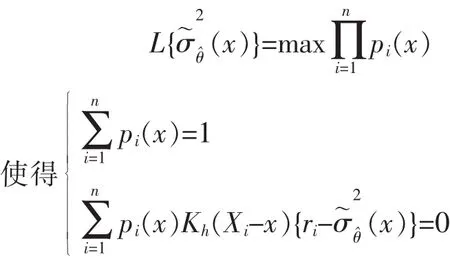
通過引入Lagrange乘子,得最優權重為：

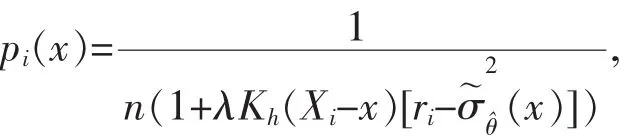
因為相應于σ2（x）的非參數估計量的最大經驗似然在ωi（x）=n-1處達到,因此（x）的對數經驗似然比為:

為了將經驗似然比統計量推廣成為擬合優度的一個全局的度量,文中考慮如下的能夠全局度量擬合優度的經驗似然基礎上的統計量:

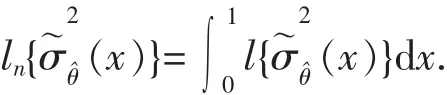
3 假設條件與主要結果

文中的理論結果建立在如下的條件之上.

A1：核函數K（·）和W（·）是正的、連續、可微、對稱的密度函數,具有緊支撐[-1，1],并且K（·）是Lipschitz連續的,

A2：當n→∞時，h→0，h1→0，nh→∞，nh1→∞，并且h=O（n-1/5）.

A3：函數f（·），m（·）和σ2（·）在區間I上具有連續的二階導數,且f（·）和σ2（·）在區間I上有界.

A5：Δn（x）關于x和n是一致有界的,并且原假設H0和備擇假設H1之間的差異的階數Cn=n-1/2h-1/4.

A6：令ηi=ri-σ2（Xi），對某個a0〉0,假設有且對某個k〉1有<∞.另外，

中Ωi-1為由生成的σ-域.

A7：給定Y的X的條件密度，fX|Y<∞.對任意l〉1,給定（Y1，Yl）的（X1，Xl）聯合條件密度是有界的,并且對t〉s〉1,（X1，Y1，Xs，Ys，Xt，Yt，）是連續有界的.

A8：過程{Xi，Yi}是嚴平穩和α混合的，并且對某個α〉0和ρ∈（0，1）,混合系數滿足α（k）≤aρk.

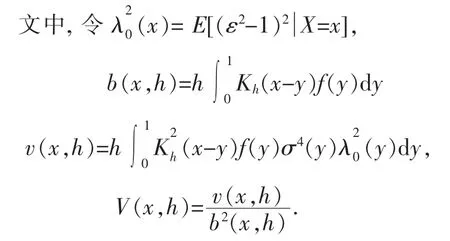
推論1假設條件A1～A8成立,則當n→∞時,有

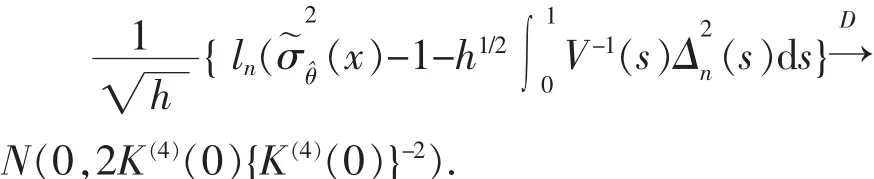
4 引理與證明

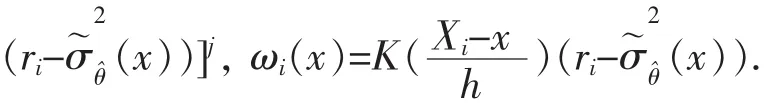
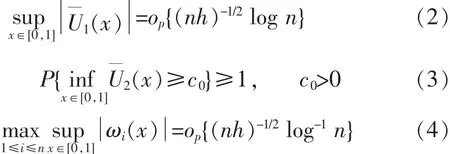
上述式（2）～式（4）的證明與文獻[12]中引理1的證明類似,此處略.

定理1的證明：設γ（x）為定義在[0，1]上的隨機過程，δn為一序列,文中用γ（x）=p（δn）和γ（x）=（δn）分別表示=op（δn）.

所以由引理1可得

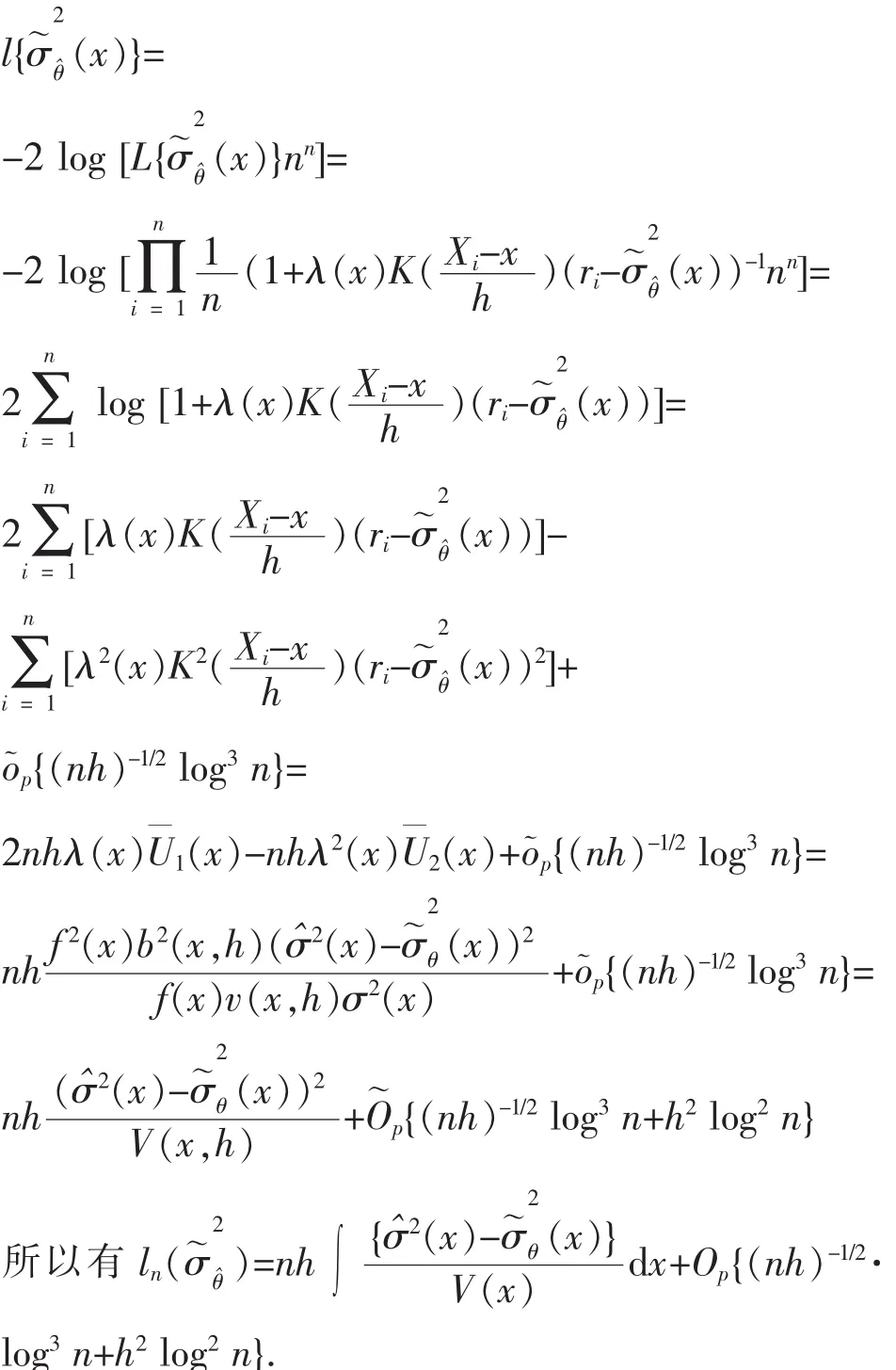
推論1的證明:由定理1的證明可得.

5 結論

文中考慮了異方差回歸模型中條件方差函數的經驗似然基礎上的擬合優度檢驗問題,在構造經驗似然統計量時,條件異方差函數σ2（x）的非參數估計量使用的是Nadaraya-Watson估計量,即局部常數估計量.但眾所周知,Nadaraya-Watson估計量會產生較大的邊界偏差,而具有如下形式的局部線性估計量能解決邊界偏差較大問題:

[1]Robert F Engle.Autoregressive conditional heteroscedasticity with estimatesofthevarianceofUnitedKingdominflation[J].Econometrica,1982,50(4):987-1008.

[2]MilanBorkovec.Asymptoticbehaviorofthesampleauto covariance and auto correlation function of the AR(1)process with ARCH(1)[J].Bernoulli,2001,7(6):847-872.

[3]Borkovec M,Klüppelberg C.The tail of the stationary distribution ofanautoregressiveprocesswithARCH(1)errors[J].AnnalsofApplied Probability,2001,11(4):1220-1241.

[4]唐明田,王允艷.隨機環境下非線性時間序列模型的漸近行為[J].江西理工大學學報,2011,32（1）:78-80.

[5]Federico M Bandi,Peter C B Phillips.Fully nonparametric estimation of scalar diffusion models[J].Econometrica,2003,71（1）:241-283.

[6]Bernt Фksendal.Stochastic differential equations:An introduction with applications[M].New York:Springer,2005.

[7]Wang Y Y,Zhang L X.Tang M T.Re-weighted functional estimation of second-order diffusion processes[J].Metrika,2011,75（8）：1129-1151.

[8]Dag Tjφtheim.Nonlinear time series:a selective revie w[J].Scandinvian Journal of Statistics,1994,21（2）：97-130.

[9]Owen A B.Empirical likelihood[M].London:Chapman&Hall,2001.[10]Qin J,Lawless J.Empirical likelihood and general estimation equations[J].The Annals of Statistics,1994,22(1):300-325.

[11]Art Owen.Empirical likelihood ratio confidence regions[J].The Annals of Statistics,1990,18(1):90-120.

[12]Chen S X,H?rdle W,Li M.An empirical likelihood goodness-offit test for time series[J].Journal of the Royal Statistical Society:Series B,2003,65(3):663-678.

[13]Hjellvik V,Yao Q W,Tjφstheim D.Linearity testing using local polynomial approximation[J].Journal of Statistical Planning and Inference,1998,68（2）:295-321.

[14]Fan J,Gijbels I.Local polynomial modeling and its applications[M].London:Chapman&Hall,1996.

[15]Fan J,Zhang C.A re-examination of diffusion estimations with applications to financial model validation[J].Journal of the American Statistical Association,2003,98：118-134.

An empirical likelihood goodness-of-test for heteroscedastic regression models

TANG Ming-tian,WANG Yun-yan

（Faculty of Science,Jiangxi Univeisity of Sciences and Technology,Ganzhou 341000,China）

Since conditional heteroscedasticity is often used in modelling and understanding the variability of statistical data,the conditional variance function in heteroscedastic regression models is taken into consideration,and a nonparametric test is constructed in the article to test the conditional variance function variance function being a known parametric form indexed by a vector of unknown parameters.The empirical likelihood technique is used to construct test procedure for a goodness-of-fit of a heteroscedastic regression model because the empirical likelihood method has two attractive features.One is its automatic consideration of the variation associated with the nonparametric fit due to the empirical likelihood＇s ability.The other one is that the asymptotic distributions of the test statistic are free of unknown parameters which avoid secondary plug-in estimation.The asymptotic null distribution of the proposed test statistic is established.

conditional variance function;empirical likelihood;goodness-of-fit test;Nadaraya-Watson estimator

O211.4

A

2012-06-28

江西省教育廳青年科學基金(GJJ12356)

唐明田（1981-），男，講師，主要從事非參數統計推斷等方面的研究，E-mail：mtt_csu@126.com.

2095-3046（2012）05-0074-04