一類分數階耦合系統多點邊值共振問題解的存在性

張 寧，張 娣，史小藝

(1.中國礦業大學理學院，江蘇徐州 221116;2.中國礦業大學管理學院，江蘇徐州 221116)

0 引言

近些年來，分數階導數及分數階微分方程在科學、工程和數學等領域得到了重要應用.在分數階微分方程邊值問題研究上，科研人員獲得了不少研究成果［1-9］.值得注意的是，分數階耦合系統多點邊值共振問題作為分數階非局部邊值問題的一種特殊情況，近年來得到許多研究人員的重視，一些學者運用Mawhin的連續性定理來研究多點邊值問題，如文獻［4］就研究了耦合系統的3點邊值共振問題，

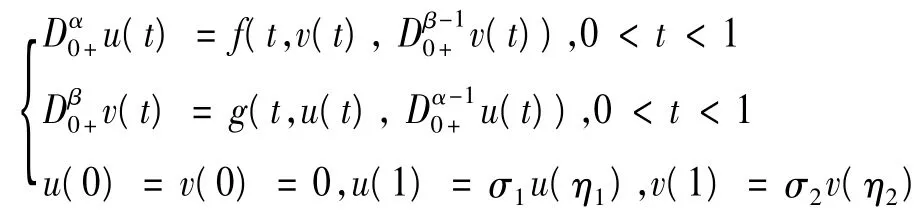
其中，1＜α，β≤2，0＜η1，η2＜1，σ1，σ2＞0，σ1ηα-11=σ2ηβ-12=1，f，g:［0，1］×R2→R連續，Dα0+是標準Riemann-Liouville分數階導數.

受其啟發，本文研究分數階非線性微分方程耦合系統多點邊值共振問題，

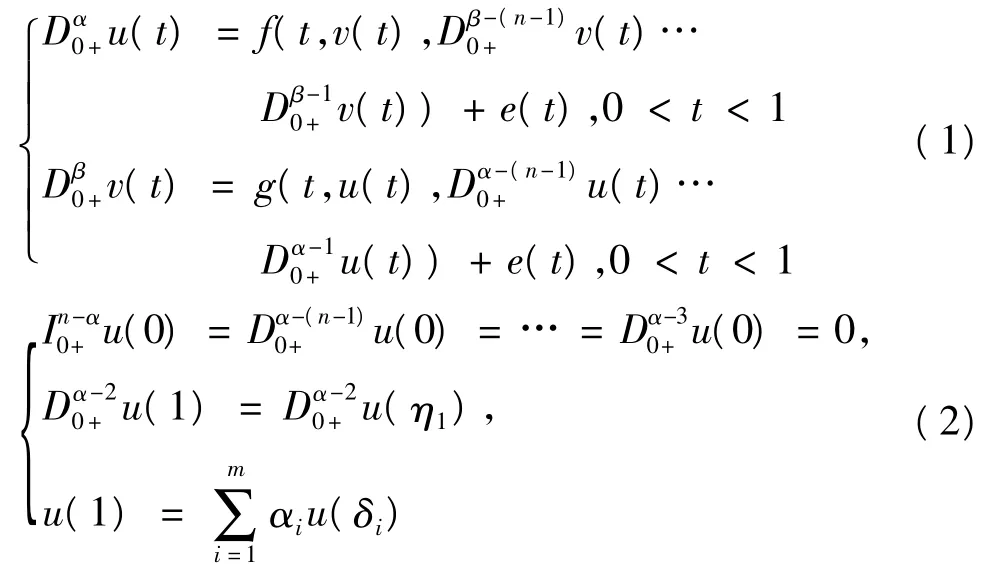
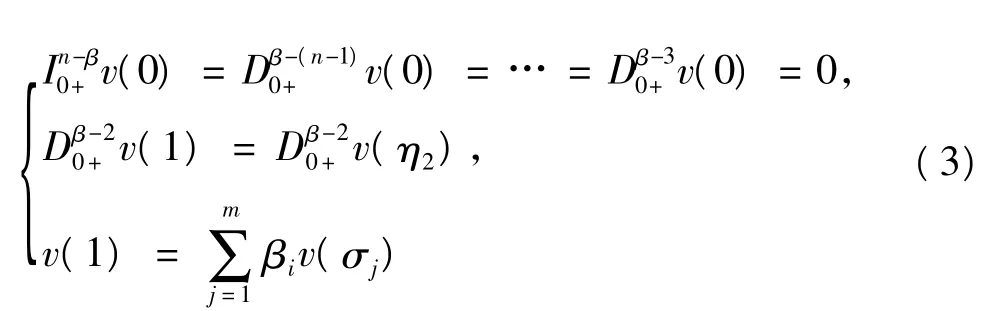
其中，n＞2是自然數，n-1＜α，β≤n，0＜η1，η2＜1，0＜δ1＜…＜δm＜1，0＜σ1＜…＜σm＜1，αi，βi∈R，Dα0+和Iα0+分別是標準Riemann-Liouville分數階導數和積分，f，g:［0，1］×Rn→R滿足Caratheodory條件，e(t)∈L1［0，1］.令，

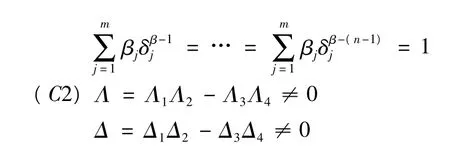
1 預備知識

設Y，Z是實Banach空間，L:domL?Y→Z是一個指標為零的Fredholm算子，P:Y→Y，Q:Z→Z，是連續投影算子且滿足ImP=Kerl，KerQ=ImL，Y= KerL⊕KerP，Z=ImL⊕ImQ.則映射，L|domL∩KerP: domL∩KerP→ImL，是可逆的，記這個映射的逆映射為KP，令N:Y→Z是一個映射，Ω是Y的一個有界開集且滿足，domL∩Ω=＞，如果QN(Ω—)有界，KP(I-Q)N:Ω—→Y是緊的，則稱N是L-緊的，設J: ImQ→KerL是一個線性同構.

定義1［1］函數y:(0，+∞)→R的α階Riemann-Liouville分數階積分為，

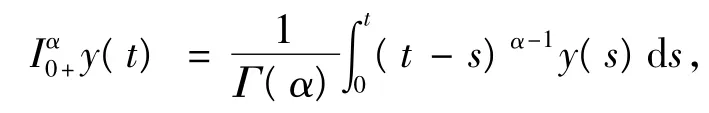
其中，α＞0，Γ(·)為Gamma函數.

定義2［1］連續函數y:(0，+∞)→R的α階Riemann-Liouville分數階導數為，

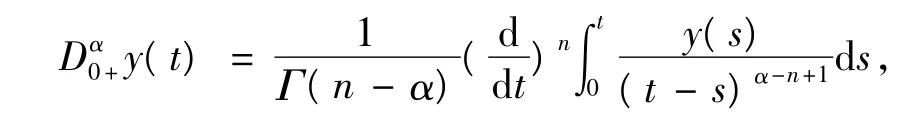
其中，α＞0，Γ(·)為Gamma函數，n=［α］+1.

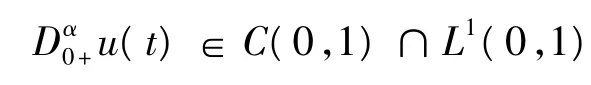
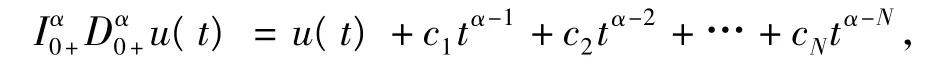
其中，N為大于或等于α的最小整數.

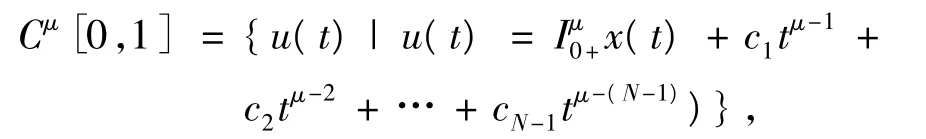
其中，x∈C［0，1］，ci∈R，i=1，2，…，N-1，其范數為，

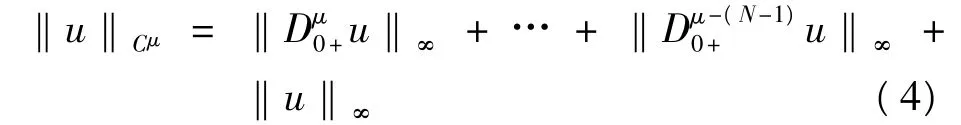
易證得，Cμ［0，1］是Banach空間.

引理2［2］f?Cμ［0，1］是連續緊，當且僅當f一致有界且等度連續.

這里的一致有界是指存在M＞0，使得對任意u∈f有，

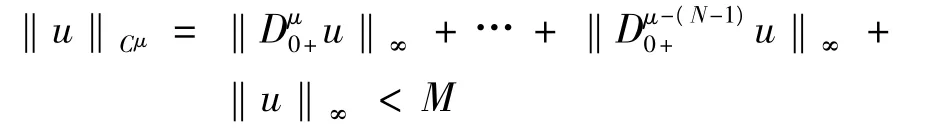
等度連續是只對?ε＞0，?δ＞0，使得，

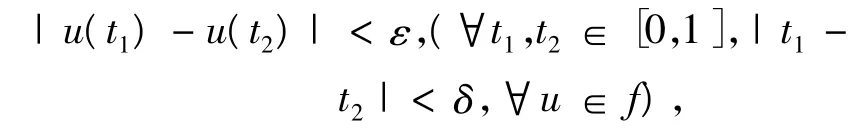
且，

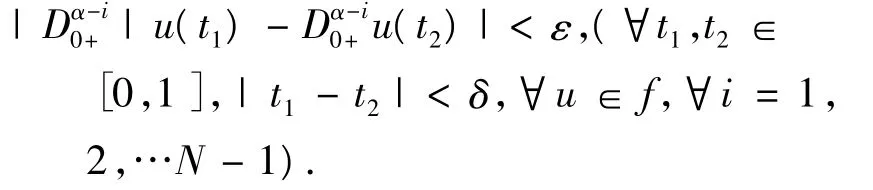
定理1［5］設Ω?Y是一個有界開集，L是一個指標為零的Fredholm算子，N是L-緊的，如果下面條件成立，

(1)Lx≠λNx，?(x，λ)∈［domLKerL∩?Ω］×［0，1］;

(2)Nx?ImL，?x∈Ker∩?Ω;

(3)deg(JQN|KerL，KerL∩Ω，0)≠0，則方程，Lx =Nx，在domL∩Ω—中至少有一個解.

2 主要結果

令Z=L1［0，1］，范數為，‖y‖∫01|y(s)|ds，Y1=Cα-1［0，1］，Y2=Cβ-1［0，1］，由式(4)知，

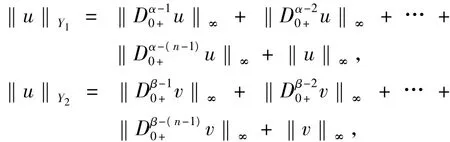
其中，Y=Y1×Y2是 Banach空間，‖(u，v)‖Y= max{‖u‖Y1，‖v‖Y2}，Z=Z1×Z1是Banach空間，‖(x，y)‖Z=max{‖x‖1，‖y‖1}.

定義L1是從domL1∩Y1到Z1的線性算子，

domL1={u∈Cα-1［0，1］|Dα0+u∈L1［0，1］，u滿足式(2)}，L1u=Dα0+u，u∈domL1.

定義L2是從domL2∩Y2到Z1的線性算子，

domL2={v∈Cβ-1［0，1］|Dβ0+v∈L1［0，1］，v滿足式(3)}，L2v=Dβ0+v，v∈domL2.

定義L是從domL∩Y到Z的線性算子，

domL={(u，v)∈Y|u∈domL1，v∈domL2}，L(u，v)=(L1u，L2v).

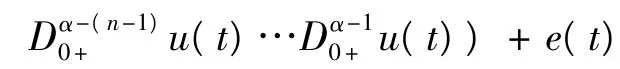
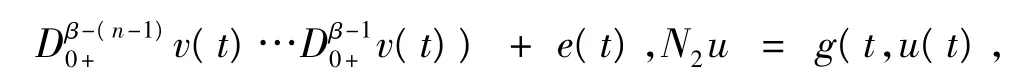
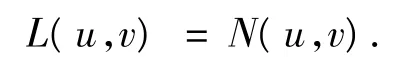
引理3 映射L:domL?Y→Z是一個指標為零的Fredholm算子.

證明 顯然，KerL1={atα-1+btα-2|a，b∈R}?R2，KerL2={ctβ-1+dtβ-2|c，d∈R}?R2，KerL= {atα-1+btα-2，ctβ-1+dtβ-2|a，b，c，d∈R}?R2×R2.

一方面，令(x，y)∈ ImL，則存在，(u，v)∈domL，使得，(x，y)=L(u，v)，即，u∈Y1，x=Dα0+u和v∈Y2，y=Dβ0+v，則由引理1可知，

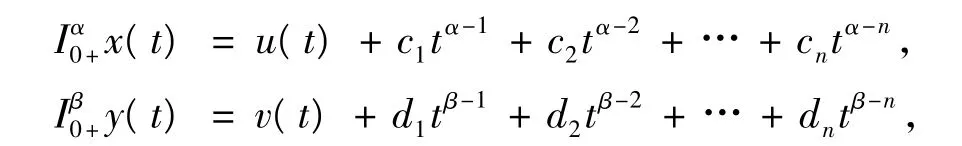
由邊值條件知，c3=c4=… =cn=0，c1，c2是任意常數，x滿足，

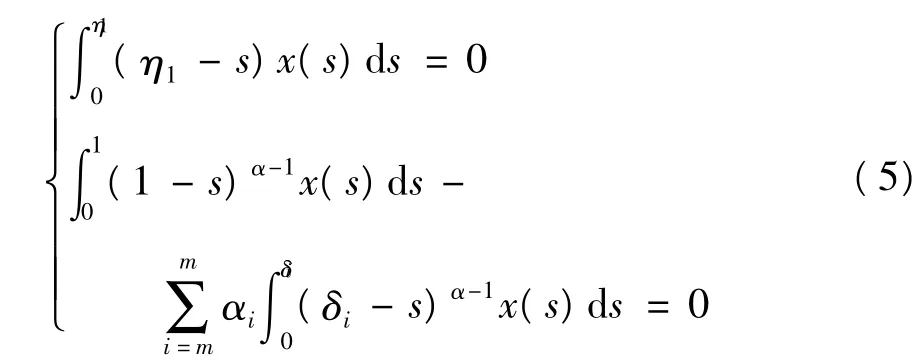
由邊值條件知，d3=d4=… =dn=0，d1，d2是任意常數，y滿足，

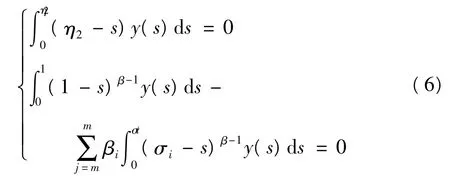
另一方面，假設(x，y)∈Z1分別滿足式(5)、(6)，令，u(t)=Iα0+x(t)，v(t)=Iβ0+y(t)，那么，u∈domL1，Dα0+u(t) =x(t)和 v∈ domL2，Dβ0+v(t) = y(t)，即，(x，y)∈ImL.因此，可得到，ImL={(x，y)∈Z|x滿足(5)，y滿足(6)}.

考慮定義連續線性映射，Ai，Bi，Ti，Ri，Qi:Z1→Z1，i=1，2和Q:Z→Z，

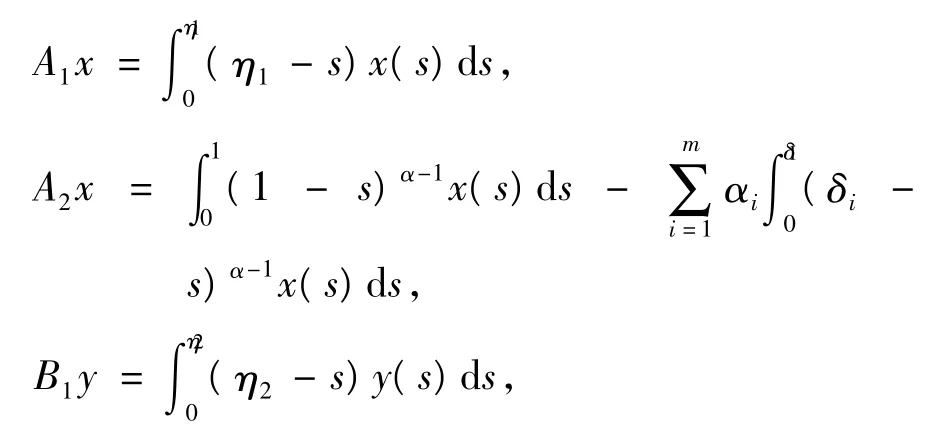
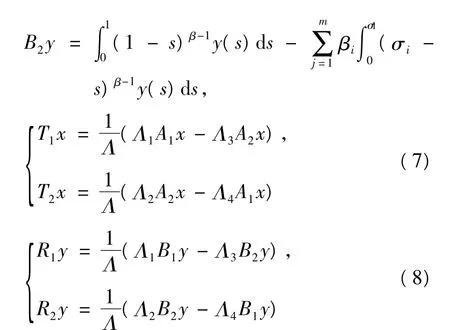
因為條件(C1)、(C2)成立，定義映射，

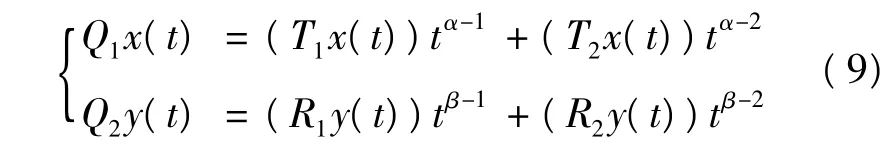
顯然，dimImQ1=dimImQ2=2.

由條件(C1)、(C2)，注意到，

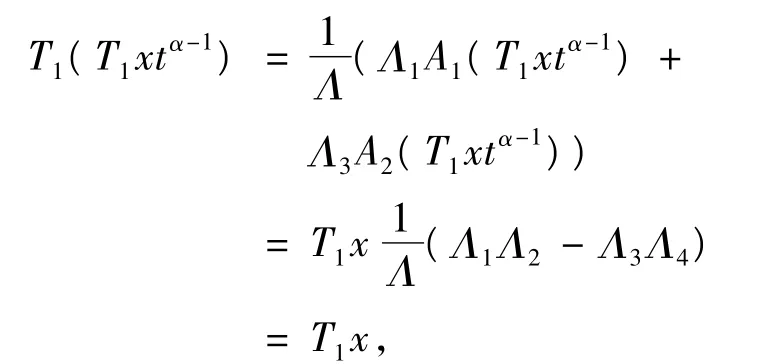
同理可得，

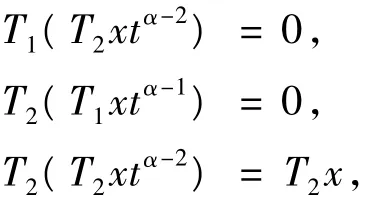
所以，對于x∈Z1，有，

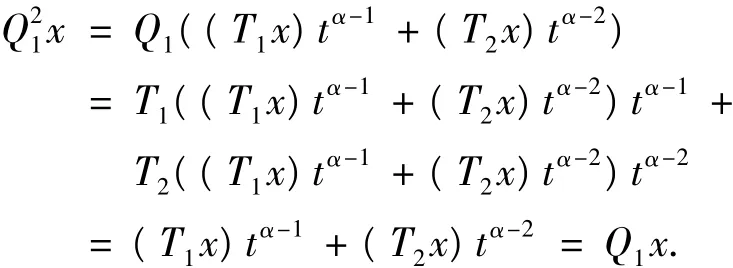
即，Q1是連續線性投影算子.

同理可知，Q2也是連續線性投影算子.所以，Q(x，y)=(Q1x，Q2y)是一個連續線性投影算子.

注意到(x，y)∈ImL可推得，Q(x，y)=(Q1x，Q2y)=(0，0).反過來說，如果式子Q(x，y)=(0，0)成立，則有，

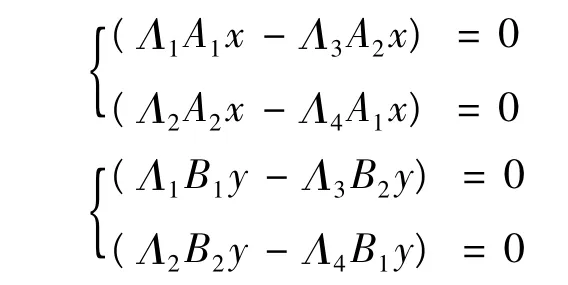
但是，

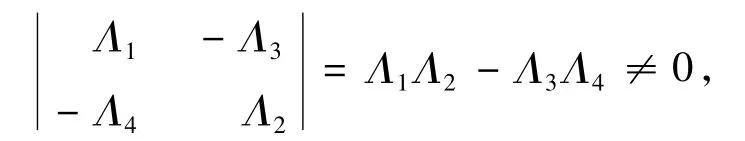
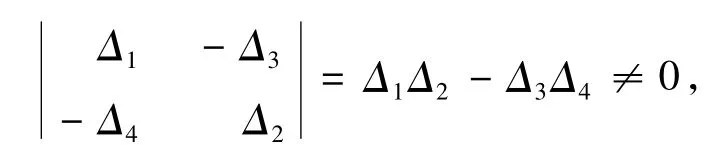
故一定有，Aix=Biy=0，i=1，2，即，(x，y)∈ImL，得到，KerQ=ImL.

令(x，y)∈Z，則，(x，y)=((x，y)-Q(x，y)) +Q(x，y)，使得，((x，y)-Q(x，y))∈KerQ=ImL，Q(x，y)∈ImQ成立.因此，Z=ImL+ImQ.再令(x，y)∈ImL∩ImQ，假設，(x，y)=(atα-1+btα-2，ctβ-1+dtβ-2)在［0，1］上不同時為0，因為(x，y)∈ImL，即x滿足(5)，y滿足(6)，可得到，a=b=c=d=0，矛盾，所以，ImL∩ ImQ={0，0}.即，Z=ImL⊕ImQ.現在，IndL=dimKerL-codimImL=0，所以，L:domL?Y→Z是一個指標為零的Fredholm算子.

定義，P1:Y1→Y1，P2:Y2→Y2，P:Y→Y，

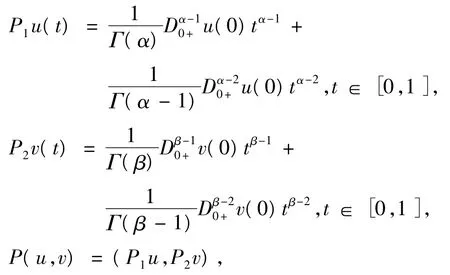
注意到，P1，P2，P是連續線性投影算子.

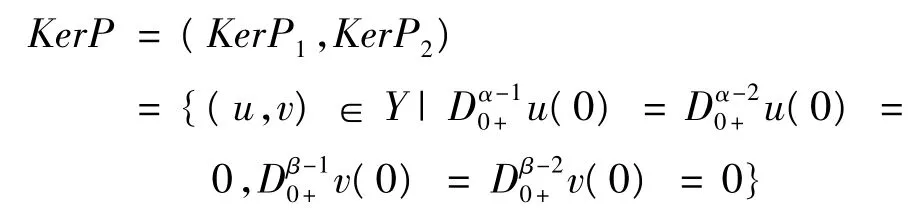
顯然，Y=kerL⊕kerP.

定義KP:ImL→domL∩KerP，KP(x，y)=(Iα0+x，

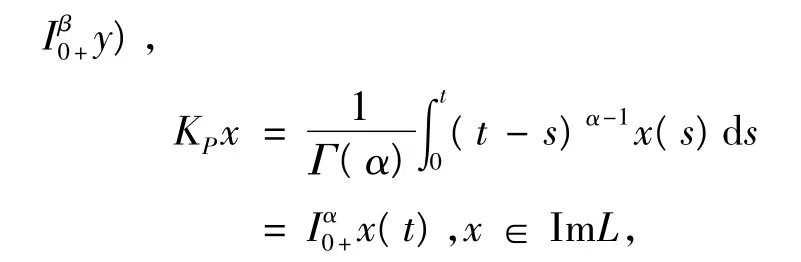
所以有，

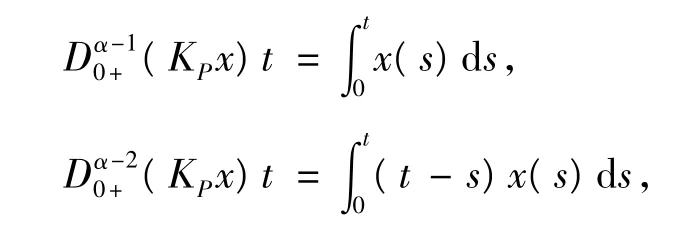
由此可知，

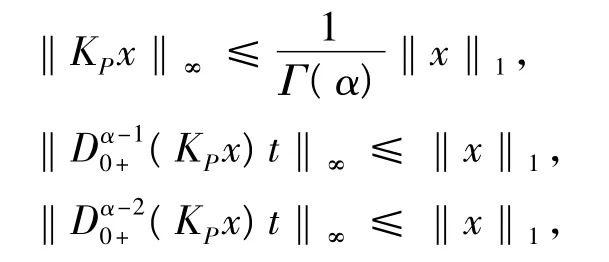
進一步可得，

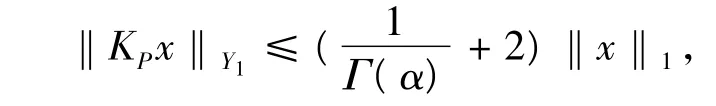
同理，

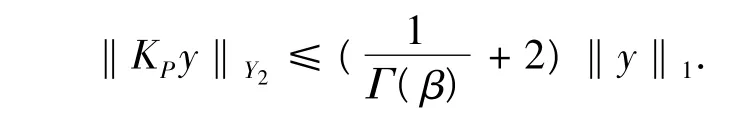
所以，

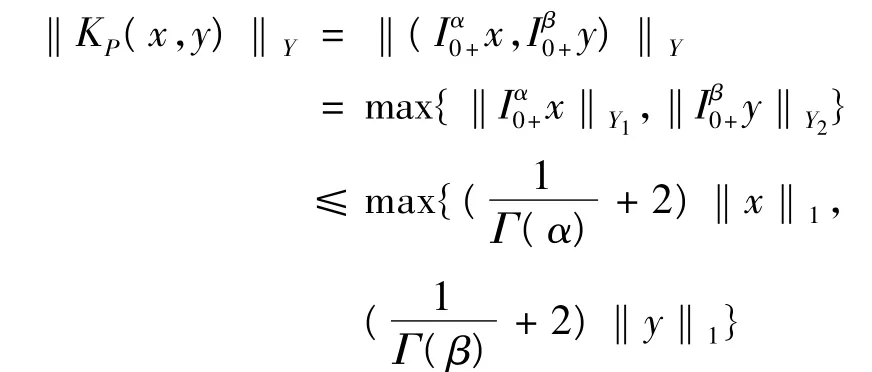
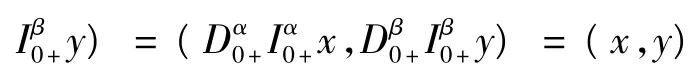
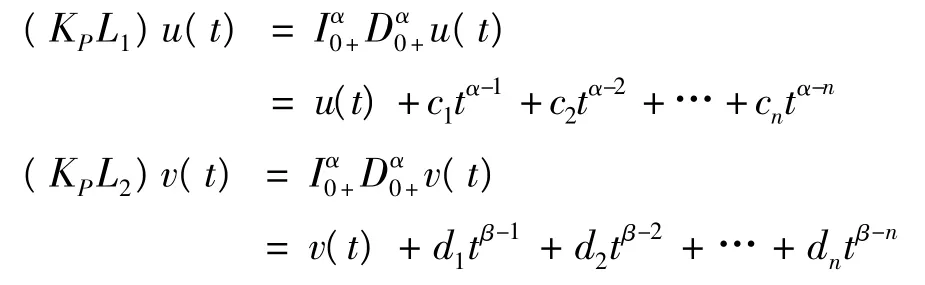
結合式(2)、(3)，可知，ci=0，di=0，i=1，…，n.即，(KPL)(u，v) = (u，v)，因此，KP=［L |domL∩KerP］-1.由式(7)、(8)、(9)可知，

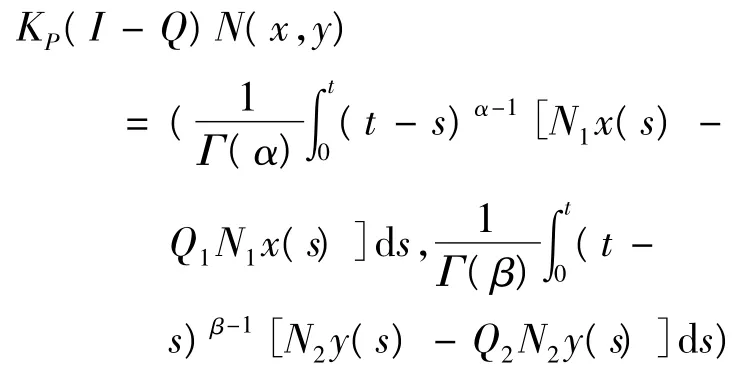
結合引理2，可得到下面的引理.

引理4 KP(I-Q)N:Y→Y是全連續算子.設，

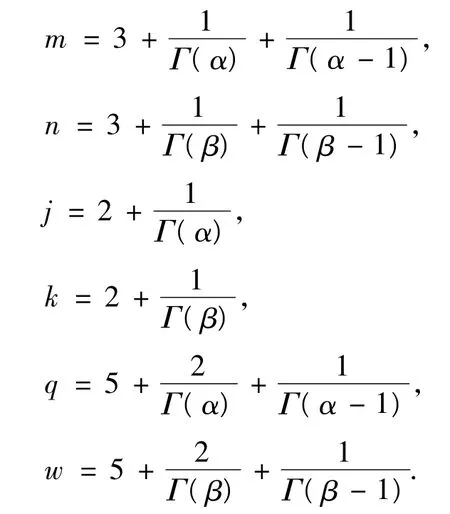
(A1) 存 在 函 數，a1(t)，b1(t)，…，bn-1(t)，c1(t)，r1(t)∈L1［0，1］，θ1∈［0，1］，使得對于(x，y1，…，yn-1)∈Rn，t∈［0，1］，有，

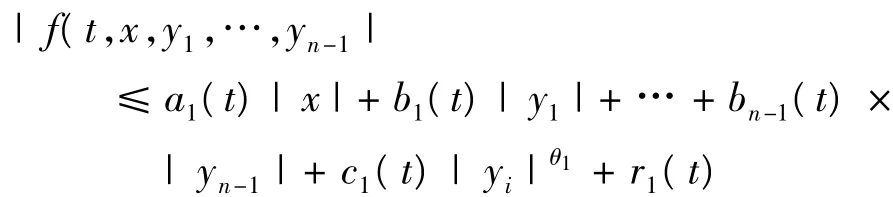
存在函數，a2(t)，d1(t)，…dn-1(t)，c2(t)，r2(t) ∈L1［0，1］，θ2∈［0，1］，使得對于(x，y1，…yn-1)∈Rn，t∈［0，1］，有，

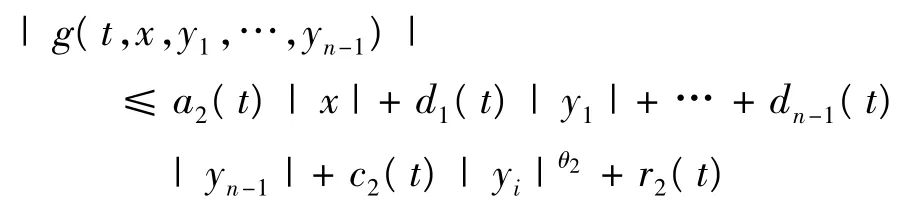
(A2)?A＞0，使得對于(u，v)∈domLkerL，t∈ ［0，1］， 滿 足，min{| D0α+-1u(t) |+ … +| D0α+-(n-1)u( t)|，D0β-+1v(t)|+…+|D0β-+(n-1)v(t)|} ＞A，有，

或，

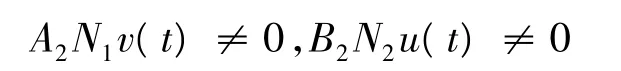
(A3)?A*＞0，使得對于a，b，c，d∈R滿足，min{a2+b2，c2+d2}＞A*有，

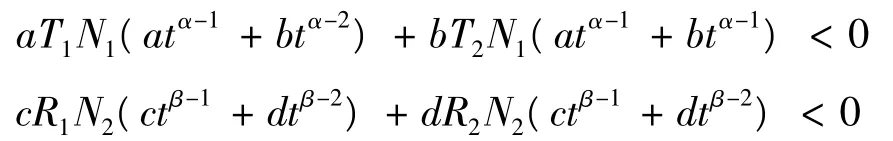
或，

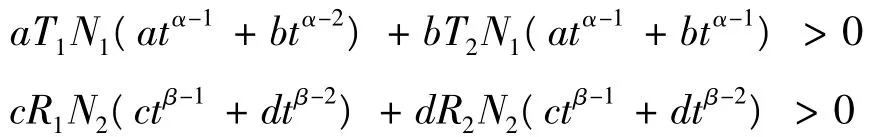
定理2 如果條件(C1)、(C2)和(A1)、(A2)、(A3)成立，并且

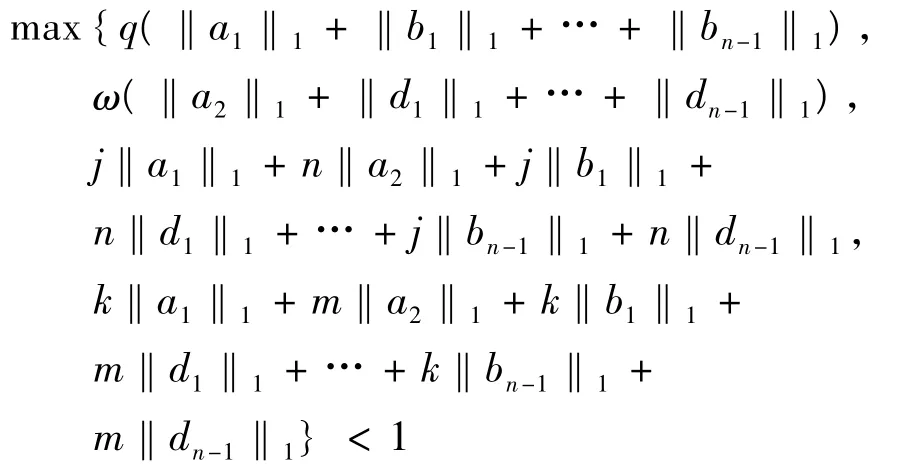
那么邊值問題(1)、(2)、(3)至少有一個解.

證明 令Ω1={(u，v)∈domLKerL:L(u，v) =λN(u，v)，λ∈［0，1］}，對于(u，v)∈Ω1，有L(u，v)=λN(u，v)，因此λ≠0，N(u，v)∈ImL=KerQ，所以，對于t∈［0，1］，有QN(u，v)=(0，0).

由Q的定義，有Q1N1v(t)=Q2N2u(t)=0.據(A2)，存在t0，t1∈［0，1］，使得，

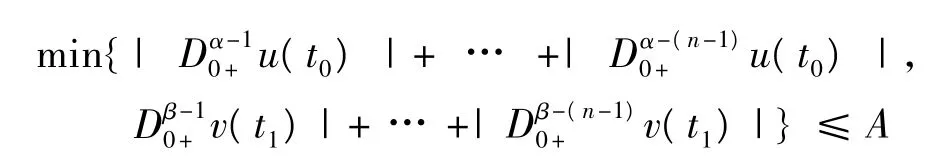
成立.

所以，

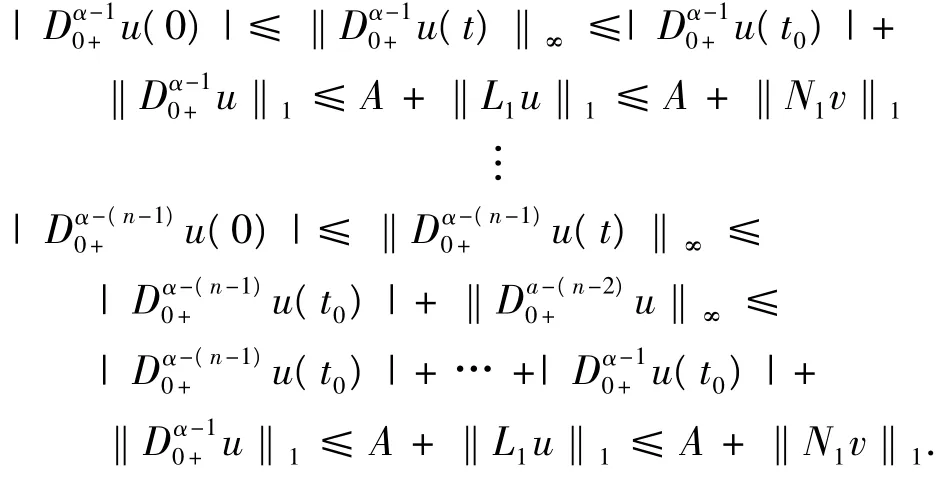
同理，

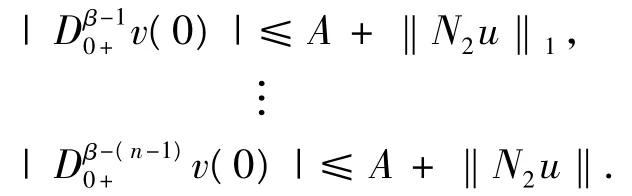
注意到，對于(u，v)∈Ω1，有(I-P)(u，v)∈domL∩KerP成立，那么，

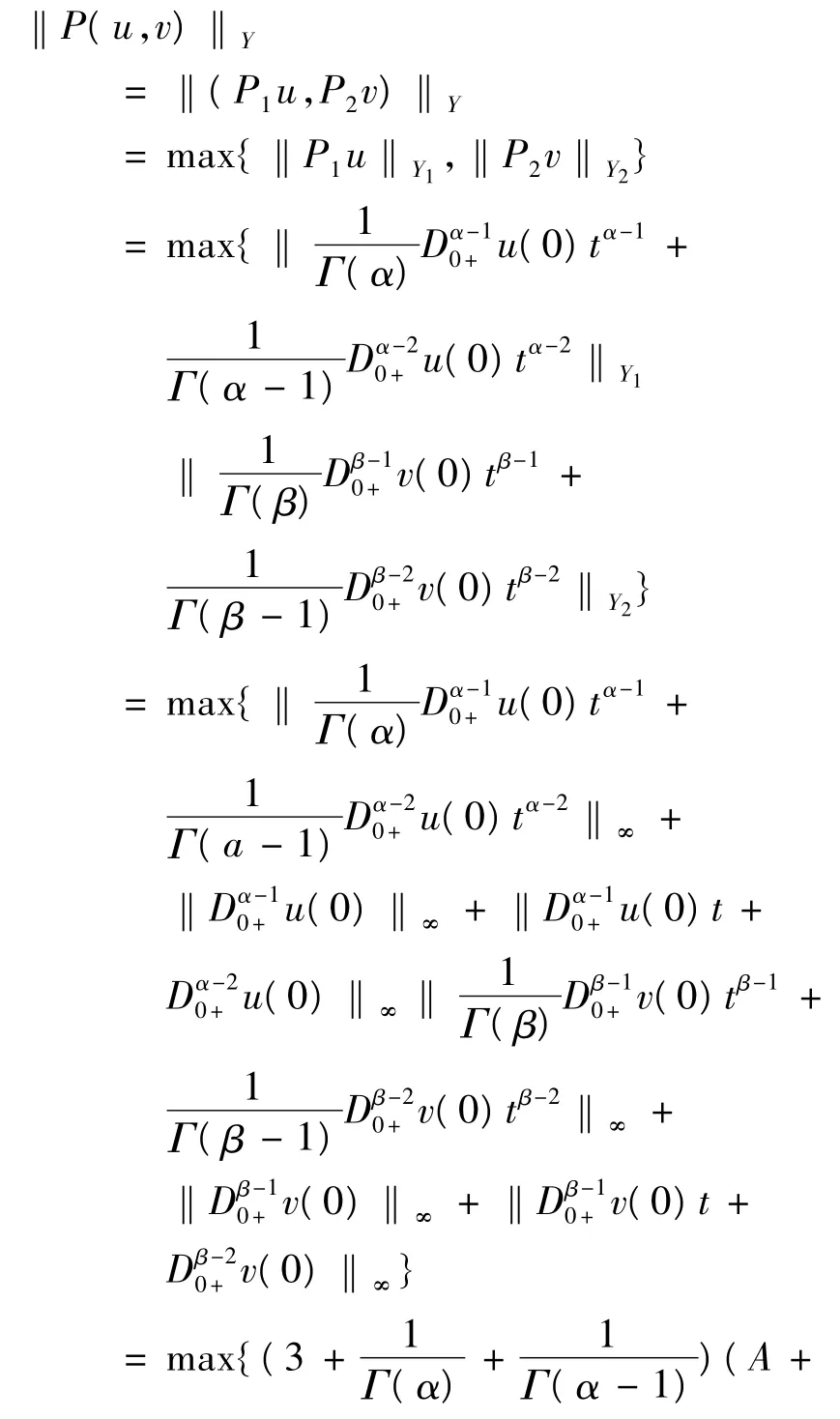
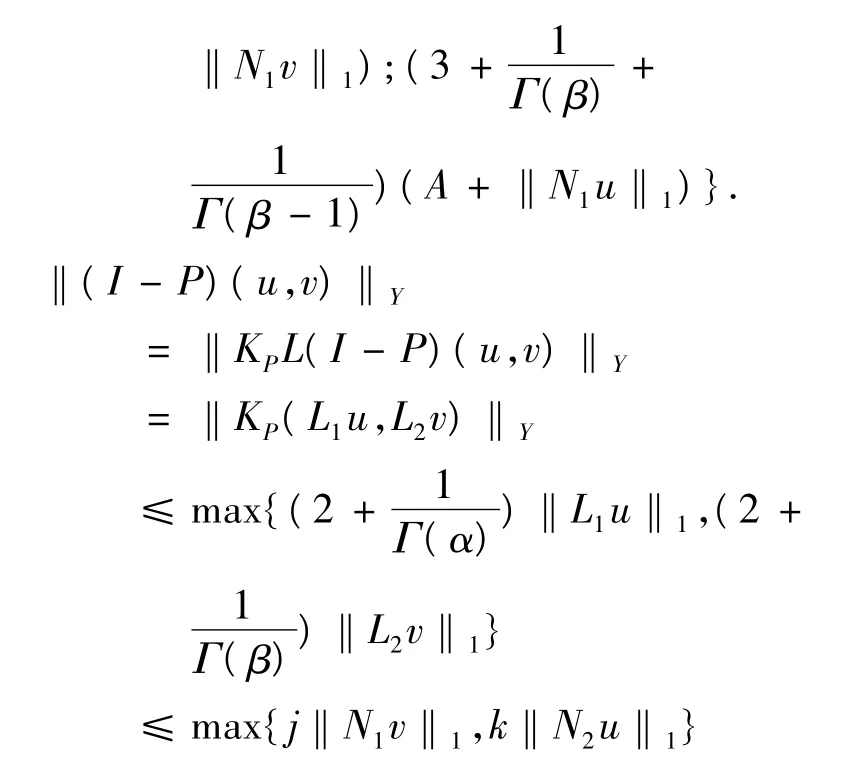
所以有，

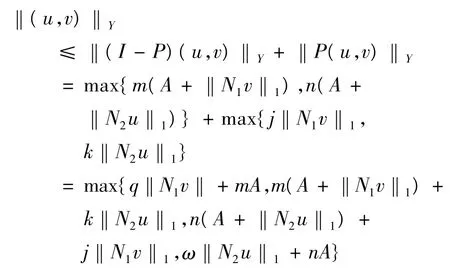
下面證明分成四部分.如果(A1)滿足，

條件1.

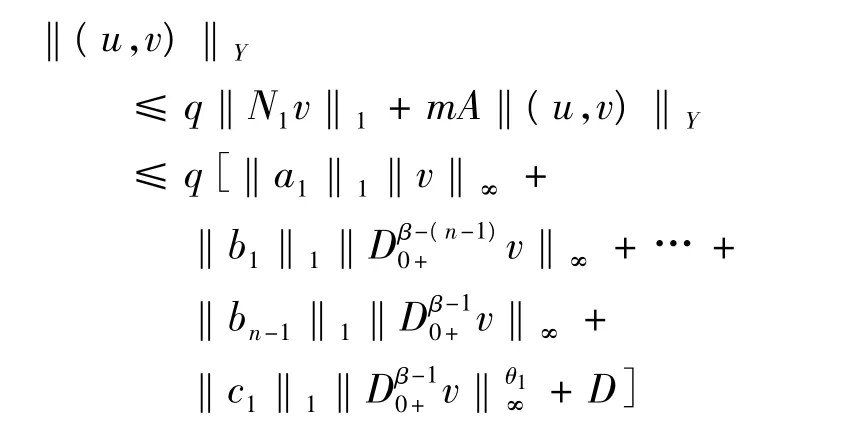
由于 ‖v‖∞，‖Dβ-(n-1)0+v‖∞，…，‖Dβ-10+v‖∞≤‖(u，v)‖Y，所以，

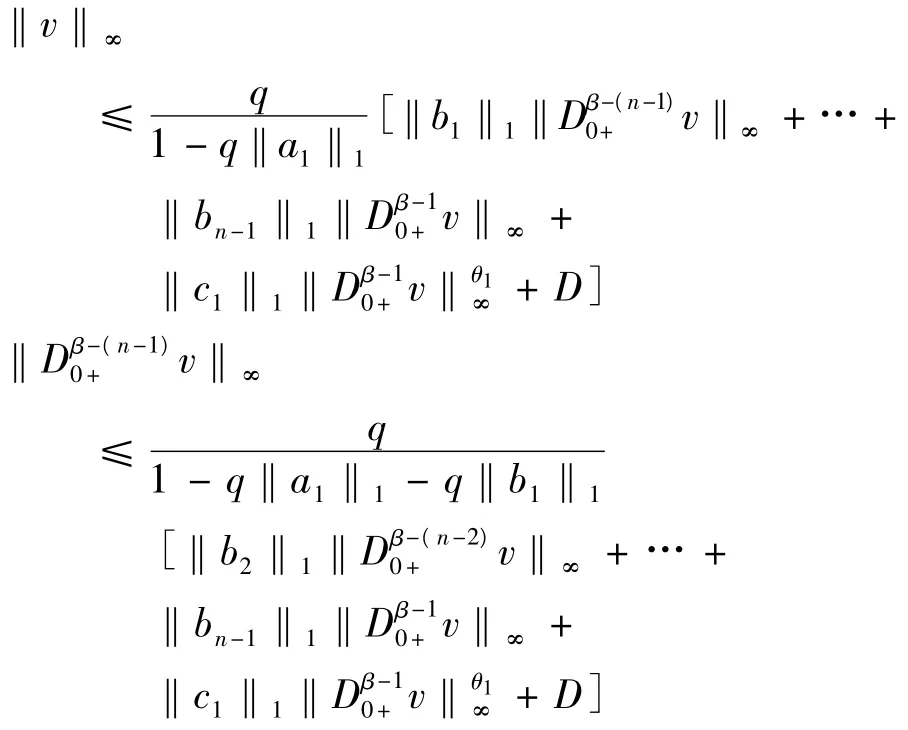
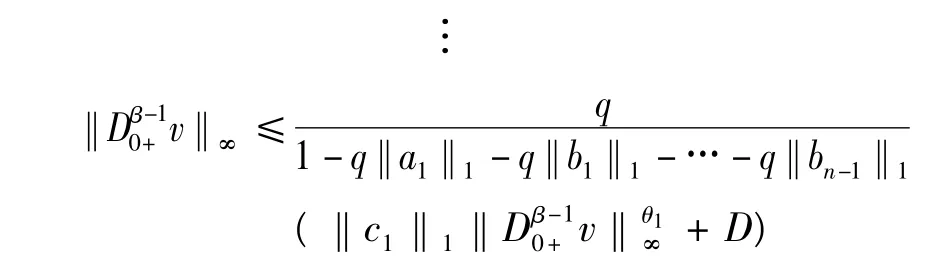
但是，θ1∈［0，1］和‖a1‖1+‖b1‖1+… +‖bn-1‖1≤，所以存在，M0，…，Mn-1＞0，使得，‖v‖∞≤ M0，‖D0β-+1v‖ ≤ M1，…，‖D0β+-(n-1)v‖ ≤Mn-1， 故 對 于， (u，v) ∈ Ω1，‖(u，v)‖Y= max{‖v‖∞，‖D0β+-1v‖∞，…，‖D0β-+(n-1)v‖∞} ≤max{M1，…，Mn-1}，即Ω1有界.

條件2.

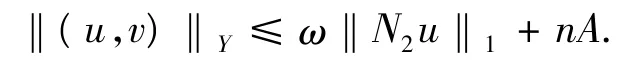
證明過程同條件1，其中，‖a2‖1+‖d1‖1+…

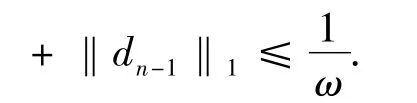
條件3.

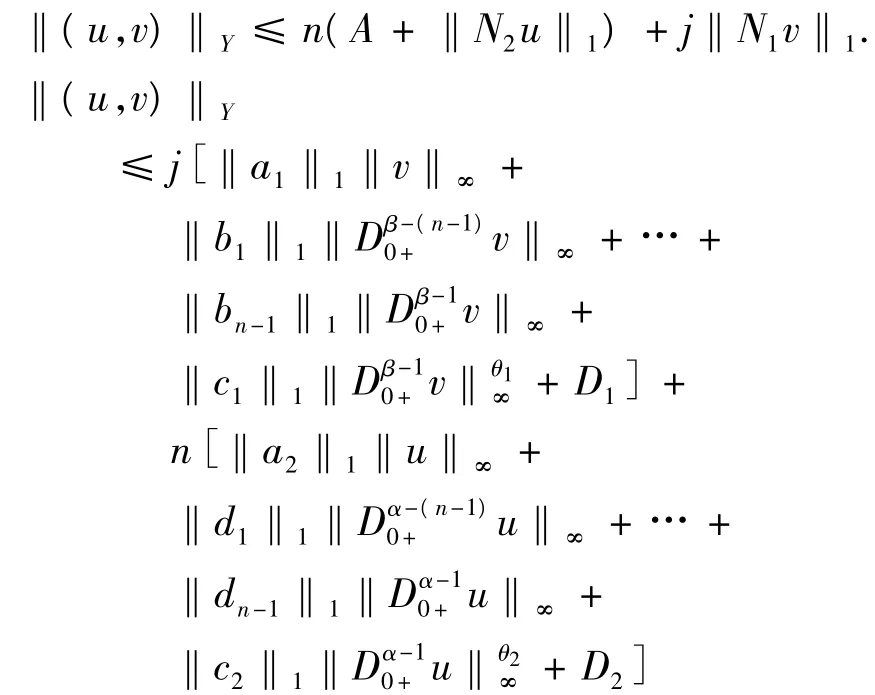
其中，D1=‖r1‖1+‖e‖1，D2=‖r2‖1+‖e‖1+A.

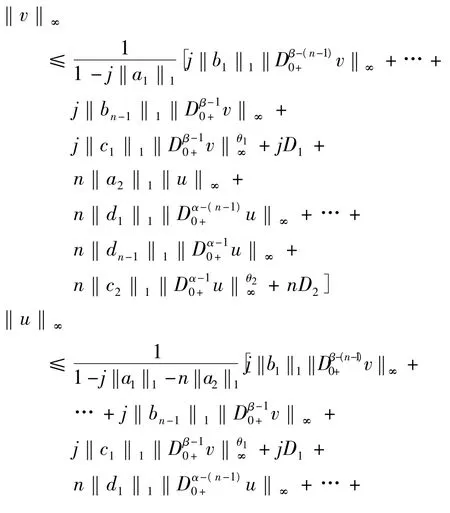
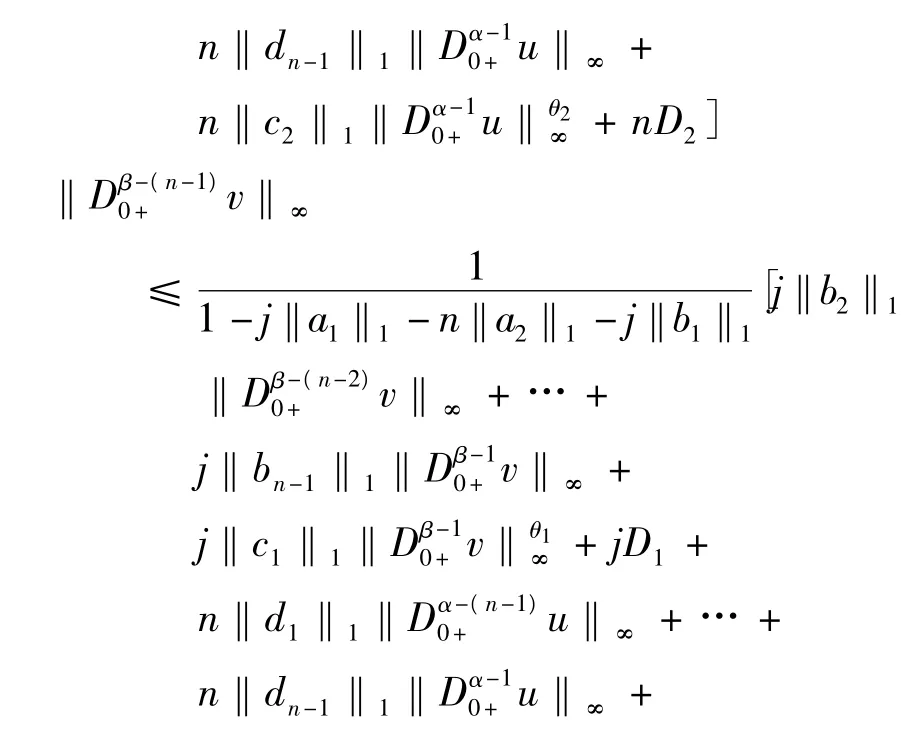
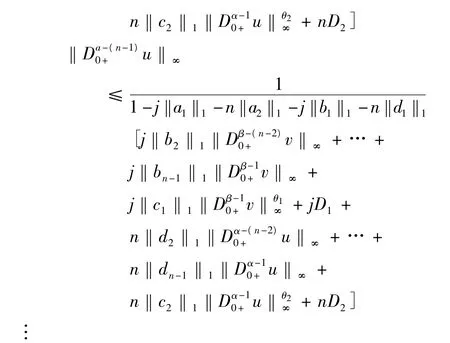
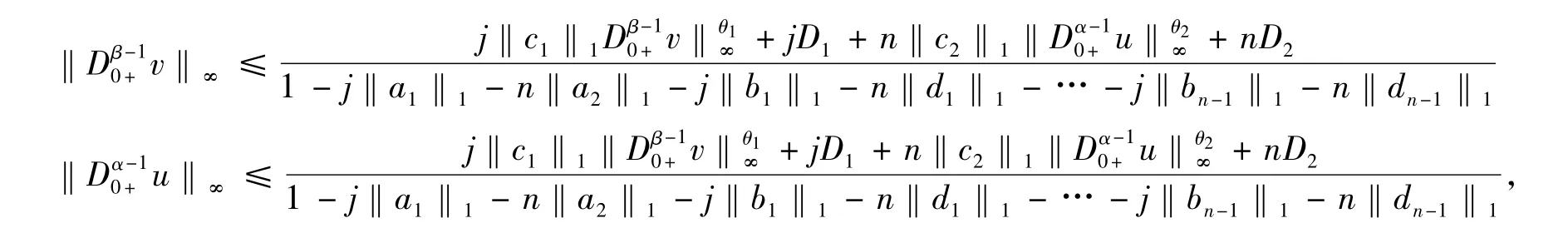
如果，j‖c1‖1Dβ-10+v‖θ1∞≤n‖c2‖1‖Dα-10+u‖θ2∞，有，

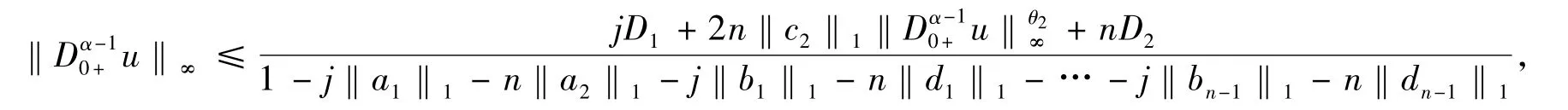
但是，θ2∈［0，1］和 j‖a1‖1+n‖a2‖1+ j‖b1‖1+n‖d1‖1+…+j‖bn-1‖1+n‖dn-1‖1＜1

所以存在，M0，…，Mn-1，M′0，…，M′n-1＞0，使得，

如果，j‖c1‖1‖Dβ-10+v‖θ1∞≥n‖c2‖1‖Dα-10+u‖θ2∞，同樣可證明Ω1有界.

條件4.

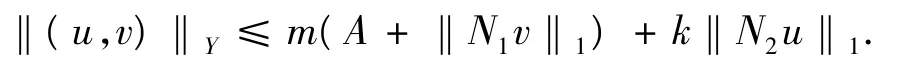
證明過程同條件3，其中，k‖a1‖1+m‖a2‖1+ k‖b1‖1+m‖d1‖1+…+k‖bn-1‖1+m‖dn-1‖1

＜1.

令，Ω2={(u，v)∈KerL:N(u，v)∈ImL}，對于，(u，v)∈Ω2，(u，v)∈KerL={(u，v)∈domL| (atα-1+btα-2，ctβ-1+dtβ-2)，a，b，c，d∈ R，t∈［0，1］}和QN(u，v)=(0，0)，因此，

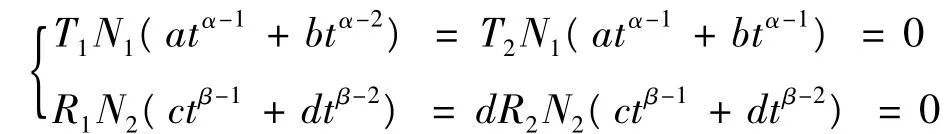
由(A3)，min{a2+b2，c2+d2}≤A*，即Ω2有界.

定義線性同構J:ImQ→KerL，

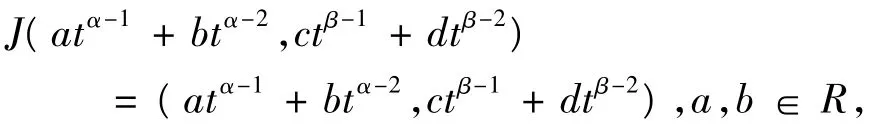
若(A3)第一部分成立，令，Ω3={(u，v)∈KerL:-λJ-1(u，v)+(1-λ)QN(u，v)=(0，0)，λ∈［0，1］}，對于任意，(u，v)=(atα-1+btα-2，ctβ-1+

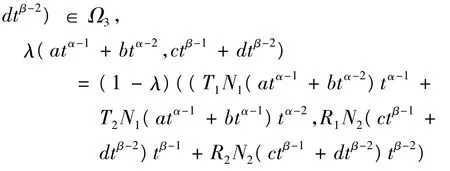
如果λ=1，那么a=b=c=d=0;如果，min{a2+b2，c2+d2}＞A*，那么根據(A3)，

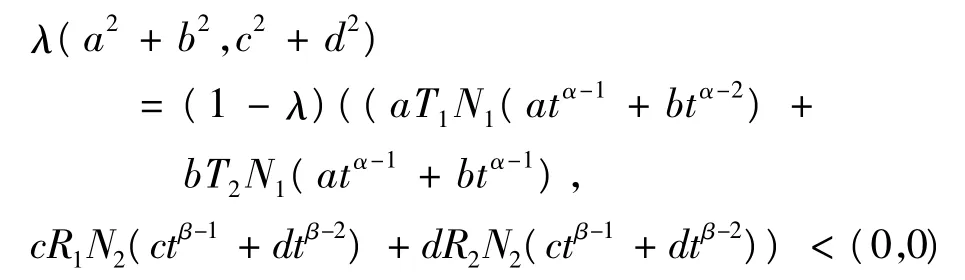
設Ω是Y中的有界開集，使得U3i=1Ω—i?Ω.根據引理4，映射KP(I-Q)N:Y→Y是緊的，因此，N在Ω—是L-緊的.根據上述論述，定理1中的(1)，(2)已滿足，最后，我們將證明定理1的(3)滿足，令，H((u，v)，λ)=±λJ(u，v)+(1-λ)JQN(u，v)，通過上面論述，可知，對于(u，v)∈?Ω∩KerL，H((u，v)，λ)≠0.所以，

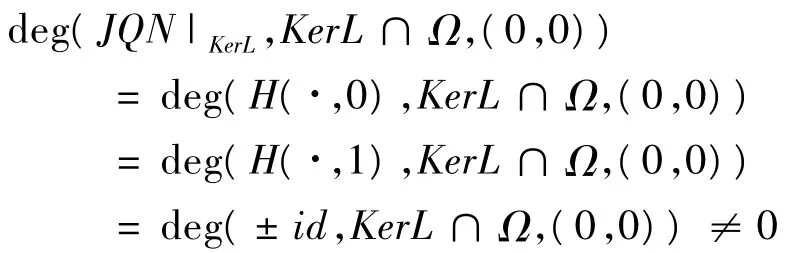
由定理1可知，L(u，v)=N(u，v)在domL∩Ω—上至少有一個解，即邊值問題(1)、(2)、(3)在Y上至少有一個解.

得出矛盾，若(A3)的另一部分成立，

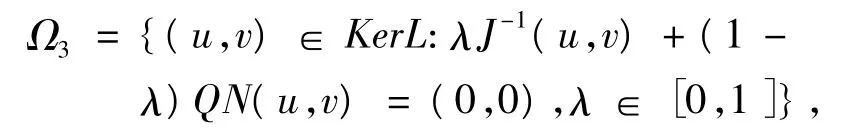
同樣可得出矛盾.因此，可推知，

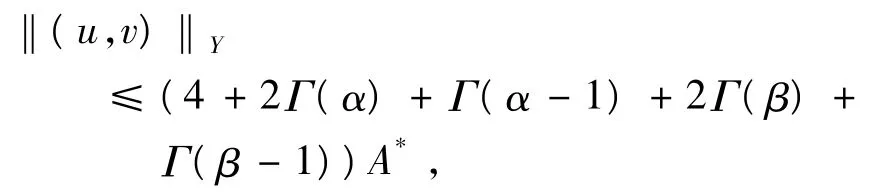
即Ω3有界.

［1］Bai Z B，Lu H S.Positive Solutions for Boundary Value Problem of Nonlinear Fractional Differential Equation［J］.Journal of Mathemalical Analysis and Applications，2005，311(2): 495-505.

［2］Zhang Y H，Bai Z B.Existence of Solutions for Nonlinear Fractional Three-point Boundary Value Problems at Resonance［J］.Journal of Applied Mathematics Computing，2011，36(1):417-440.

［3］Bai Z B，Zhang Y H.The Existence of Solutions for a Fractional Muti-point Boundary Value Problems［J］.Computers and Mathematics with Applications，2010，60(8):2364-2372.

［4］Zhang Y H，Bai Z B，Feng T T.Existence Results for a Coupled System of Nonlinear Fractional Three-point Boundary Value Problems at Resonance［J］.Computers and Mathematics with Applications，2011，61(4):1032-1047.

［5］Wang G，Liu W B，Zhu S N，et al.Existence Results for a Coupled System of Nonlinear Fractional 2m-point Boundary Value Problems at Resonance［J］.Advances in Difference E-quations，2011，44(1):1-17.

［6］郭大鈞，孫經先，劉兆理.非線性常微分方程泛函方法［M］.濟南:山東科學技術出版社，2006.

［7］王剛，朱思念.一類分數階多點邊值共振問題解的存在性［J］.淮陰師范學院學報(自然科學)，2011，10(3):193-200.

［8］Bai Z B.On Solutions of some Fractional M-point Boundary Value Problems at Resonance［J］.Electronic Journal of Qualitative Theory of Differential Equations，2010，37(1):1-15.

［9］Su X.Boundary Value Problem for a Coupled System of Nonlinear Fractional Differential Equations［J］.Applied Mathematics Letters，2009，22(1):64-69.