觸發器邏輯功能轉換的兩種方法

陳海霞，叢云飛

(通化師范學院 物理系，通化 吉林 134002)

觸發器是具有記憶功能的基本邏輯單元，一個觸發器能夠存儲1位二進制信息．它是時序數字電路的最基本的單元，每個時序電路都少不了觸發器．隨著科學的進步，社會的發展，時序電路在很多領域中得到了廣泛的應用．

1 觸發器的概述

1.1 觸發器的相關概念

觸發器是個特殊的存儲過程，它的執行不是由程序調用，也不是手工啟動，而是由事件來觸發．觸發器具有兩個能自行保持的穩定狀態，用來表示邏輯狀態的0和1，或二進制數的0和1．在外界信號作用下，輸出信號可以從一個穩態轉變為另一個穩態，無外界信號作用時，輸出狀態保持不變．因此，觸發器是一種具有記憶功能的二進制存貯器件，是構成各種時序電路的基本邏輯單元，它在數字系統和計算機中有著廣泛的運用．

邏輯功能是指觸發器的次態和現態及輸入信號之間在穩態下的邏輯關系.這種邏輯關系可以用特性表(功能表)、特性方程或狀態轉換圖等給出.

電路結構是指電路中門電路的種類及組合方式. 基本RS觸發器、同步RS觸發器、主從觸發器、邊緣觸發器等是電路結構的不同形式.由于電路結構形式的不同，帶來了不相同的動作特點. 同一種邏輯功能的觸發器可以用不同的電路結構實現.反過來說，用同一種電路結構形式可以作成不同邏輯功能的觸發器.

1.2 觸發器的分類

邏輯功能的描述方法：邏輯符號、特性表、驅動表、特性方程.

按照邏輯功能的不同，可分為RS觸發器、JK觸發器、D觸發器和T觸發器等．

按觸發方式不同分為：電平觸發器、邊沿觸發器和主從觸發器．

按電路結構不同分為：基本RS觸發器、同步SR觸發器、主從觸發器、維持阻塞觸發器、邊沿觸發器、鐘控觸發器等．

按存儲數據原理不同分為：靜態觸發器和動態觸發器，靜態觸發器是靠電路的自鎖來存儲數據的，動態觸發器是靠電容存儲電荷來存儲數據的．

按構成觸發器的基本器件不同分為：雙極型觸發器和MOS型觸發器．

2 轉換的兩種方法

在現有集成觸發器的產品中，每一種觸發器都有著自己固定的邏輯功能．當今的市場提供的集成觸發器型號也是比較多的，目前生產的觸發器定型產品中以JK觸發器和D觸發器這兩大類為主，但是在實際應用中經常需要用到的是其它功能的觸發器．為了達到這些要求，可以在已有的觸發器的基礎上，給它們附加邏輯電路，利用邏輯功能轉換的方法獲得所需功能的觸發器．

圖1就是常用觸發器功能轉換的結構示意圖，由圖知道觸發器的轉換關鍵是怎樣設計附加組合邏輯電路，即轉換電路．進行設計附加組合邏輯電路的要求有：轉換前的觸發器(已有觸發器)和轉換后的觸發器(待求觸發器)特性方程相同．目前常用的有代數法和圖表法兩種轉換方法．這兩種方法也是邏輯函數化簡的兩種最常用的方法，用化簡后的表達式構成邏輯電路可節省器件，降低成本，提高工作的可靠性．

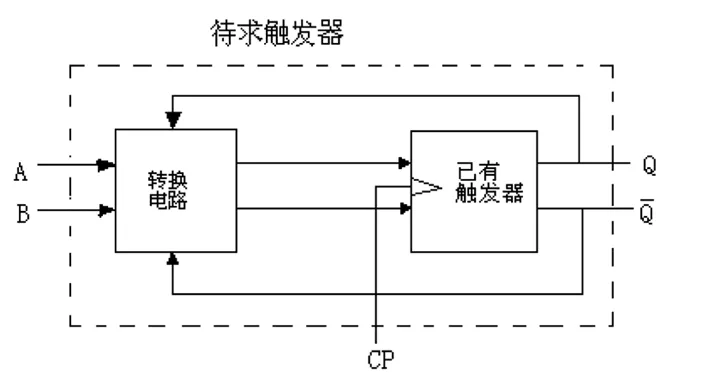
圖1 觸發器邏輯功能轉換示意圖

2.1 代數法

代數法是不同觸發器進行轉換最簡單和最直接的方法，就是利用基本邏輯公式把待求觸發器的特性方程轉換成我們已有觸發器的特性方程的形式，然后比較已有和待求觸發器的特性方程，直接推導出已有觸發器的輸入端與待求觸發器的輸入端及狀態之間的邏輯關系，從而得到所需的附加組合電路的輸入和輸出表達式，即轉換關系的邏輯表達式．

代數化簡法是根據邏輯代數的基本定律(交換律、結合律、分配律、互補律、反演律)，利用并項法、吸收法、消去法、配項法，將邏輯式化為最簡式．

轉換方法：利用令已有觸發器和待求觸發器的特性方程相等的原則，求出轉換邏輯．

轉換步驟：首先，寫出已有觸發器和待求觸發器的特性方程，變換待求觸發器的特性方程，使之形式與已有觸發器的特性方程一致．然后，比較已有和待求觸發器的特性方程，根據兩個方程相等的原則求出轉換邏輯．最后，根據轉換邏輯畫出邏輯電路圖．

例1 用RS觸發器轉換構成JK觸發器．

解：首先變換JK觸發器特性方程，使之與RS觸發器特性方程的形式一致．

再對照比較以上兩類觸發器的特性方程，可得轉換關系邏輯表達式:

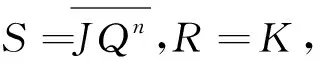
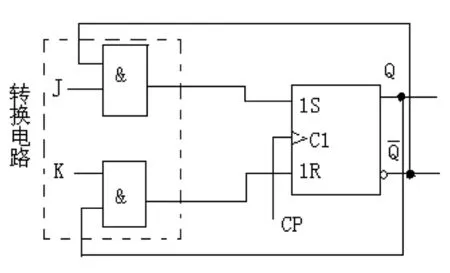
圖2 RS觸發器轉JK觸發器邏輯圖

2.2 圖表法

圖表法是另一種應用于觸發器之間邏輯轉換的重要方法，圖表法的依據是描述觸發器功能的真值表與激勵表，關鍵就是卡諾圖的利用．圖表法的過程是先列出要實現的目標觸發器的功能真值表，該真值表反映的是在不同的輸入組合及不同的狀態下，目標觸發器次態的值，再根據我們已有的觸發器的激勵表，在上述真值表中列出每一行不同狀態的轉換對應已有觸發器輸入端的值，最后以此表為依據推導出已有觸發器的輸入端與待求觸發器的輸入端及狀態之間的邏輯關系．然后利用卡諾圖求出轉換關系的邏輯表達式，最后根據邏輯表達式畫出邏輯圖．

卡諾圖是一種平面方格圖，每個小方格代表一個最小項，故又稱為最小項方格圖.卡諾圖在構造上具有以下兩個特點：n個變量的卡諾圖由2n個小方格組成，每個小方格代表一個最小項和卡諾圖上處在幾何相鄰的小方格所代表的最小項為相鄰最小項．

卡諾圖法化簡的基本步驟：首先，將邏輯函數化成與-或式；其次，繪卡諾圖和根據邏輯函數項填卡諾圖；再次，圈卡諾圈：卡諾圈包圍方格數必須滿足2n的規律(n∈R)，并要盡可能大．每個方格都應被卡諾圈包含，每個卡諾圈至少含有一個新方格；最后，得出邏輯函數化簡后的最簡與-或式．

例2 將RS觸發器轉換成JK觸發器．

解：JK觸發器特性表如表1所示：

表1 JK觸發器特性表

RS觸發器激勵表如表2所示：

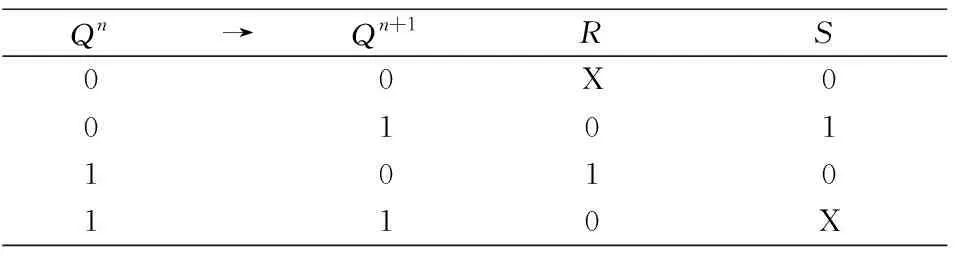
表2 RS觸發器激勵表

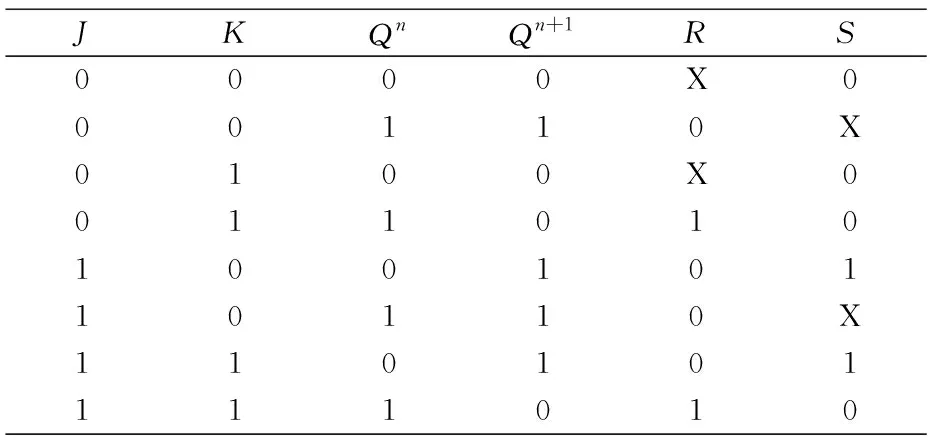
表3 RS轉JK關系真值表

我們知道RS觸發器轉換成JK觸發器必須要求兩類觸發器具有相同的狀態．

例如，對于JK觸發器，當J=K=0時，保持狀態即Qn=Qn+1．對于RS觸發器，當Qn=Qn+1=0時，狀態保持不變或狀態置0．由JK觸發器特性表和RS觸發器激勵表可以得到RS觸發器轉換JK觸發器關系真值表，如表3．

由表3我們可以作出輸出函數的卡諾圖如圖3.

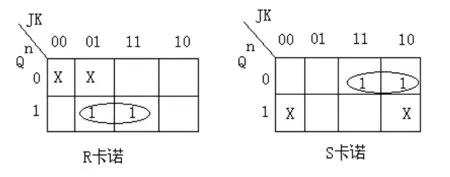
圖3 輸出函數卡諾圖

通過卡諾圖的簡化可以得到轉換邏輯關系的邏輯表達式：

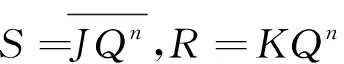
故可得到RS觸發器轉JK觸發器邏輯圖，如圖4．

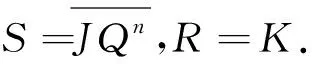
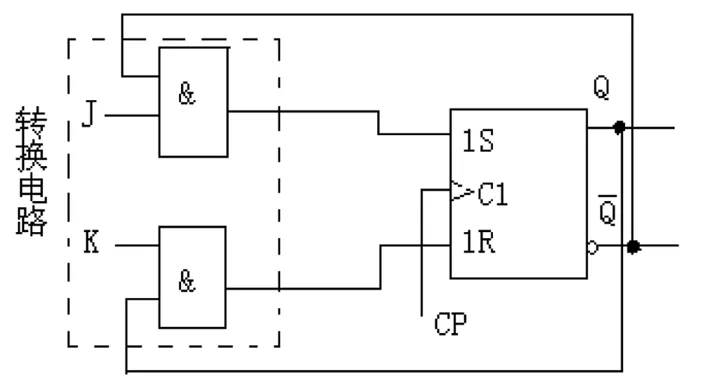
圖4 RS觸發器轉JK觸發器邏輯圖

3 結語

通過上面的述說，可以知道代數法和圖表法對于處理觸發器邏輯功能轉換問題是比較方便．在觸發器邏輯功能轉換問題轉換的過程中，可以根據實際情況選擇代數法和圖表法，如果對觸發器的特性方程掌握較好，并對邏輯函數代數化簡的方法掌握較好的情況下，可以選用代數法；如果對觸發器的特性方程不十分掌握而對轉換激勵表比較掌握，并對邏輯函數卡諾圖化簡掌握較好的情況下，可以選用圖表法．這兩種方法最終達到的目的是一致的，轉換過程有各自的特點，若能合理選擇，定能將轉換做得又快又準確．

參考文獻：

[1]梁明理.電子線路[M].北京：高等教育出版社,2008．

[2]陳其純．電子線路[M].北京：高等教育出版社,2001．

[3]蔡良偉.數字電路與邏輯設計[M].西安：西安電子科技大學出版社,2003．

[4]李大友.數字電路邏輯設計[M].北京：清華大學出版社,1997．