不可壓縮超彈性球形結構的徑向有限變形

袁學剛，杜雁芳，溫瑤

（1.大連民族學院理學院，遼寧大連116605; 2.遼寧師范大學數學學院，遼寧大連 116029）

不可壓縮超彈性球形結構的徑向有限變形

袁學剛1，杜雁芳2，溫瑤1

（1.大連民族學院理學院，遼寧大連116605; 2.遼寧師范大學數學學院，遼寧大連 116029）

早在1958年，Gent和Lindley［1］就通過實驗觀察到硫化橡膠中空穴突然形成的現象（也可見Williams和Schapery［2］）。橡膠和類橡膠材料是超彈性材料的典型代表，這類材料廣泛應用于生物醫學、航空航天和建筑工程等領域，所以由超彈性材料組成的各種結構的不穩定性問題引起了人們的普遍關注。1982年，Ball［3］應用非線性理論解決了空穴分岔問題，通過求解非線性微分方程模擬了均勻的各向同性彈性球體或柱體的內部有空穴生成的現象，并對某些特殊的超彈性材料中空穴的生成問題作了定性分析，從而奠定了分岔問題的理論基礎。此后，Horgan和Abeyaratne［4］研究了預存微孔的快速增長，并將其解釋為另一類分岔問題（也可見Sivaloganthan［5］），指出空穴是

研究了在表面拉伸載荷的作用下，各向同性不可壓縮超彈性材料組成的球形結構的有限變形問題。首先利用不可壓縮性條件及邊界條件求得了拉伸載荷和球形結構內半徑之間的關系，進而分別給出了4種球形結構（實心球體、預存微孔、球殼和球形薄膜）有限變形解的定性分析，最后結合數值算例詳細討論了材料參數和結構參數對球形結構徑向變形的影響。

不可壓縮超彈性材料;球形結構;有限變形;定性分析

本文研究了各向同性不可壓縮超彈性材料組成的球形結構的徑向有限變形問題。首先建立了不可壓縮超彈性球形結構在給定的徑向拉伸作用下球對稱變形問題的數學模型，利用逆解法求得了拉伸載荷和球形結構內半徑之間的關系。進而，分別對4種球形結構有限變形的解作了定性分析。對于由各向同性不可壓縮Ogden材料組成的實心球體和含有預存微孔的球體，分別研究了當拉伸載荷達到臨界載荷時，實心球體內部有空穴生成，預存微孔突然快速增長等問題;對于由各向同性不可壓縮Mooney－Rivlin材料的組成的球殼和球形薄膜，驗證了在表面拉伸載荷作用下，內半徑隨著拉伸載荷的增加而增加，且隨著材料參數的增加，內半徑快速增加等結論。

1 問題的數學描述

考慮由均勻的各向同性不可壓縮超彈性材料組成的球形結構，結構的外表面受到給定均布的徑向拉伸死載荷p0的作用。結構變形前、后的點的坐標分別為（R，Θ，Φ）和（r，θ，φ）。設未變形結構內部占有的區域為

式中，r（R）為待定函數，R1，R2分別表示球形結構的內外半徑。當R1=0時，球形結構表示實心球體;當R1取值充分小時，表示中心含有微孔的球體;當R1取一定大的值時（即1＜R2/R1＜+∞），表示球殼;當R1與R2充分接近時（即R2/R1→ 1），表示球形薄膜。

根據球對稱變形（2），變形張量的主伸長為

式中，W=W（λ1，λ2，λ3）為超彈性材料的應變能函數;p（R）為對應于不可壓縮條件的靜水壓力，是待定函數。

忽略體積力的作用時，球對稱變形假設下的結構滿足的平衡微分方程為

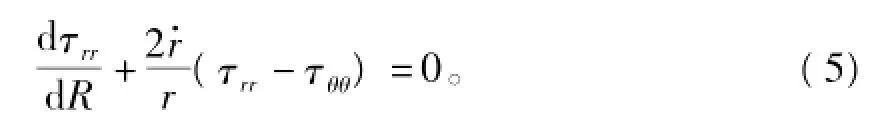
假設球形結構的外表面受到均勻分布的徑向拉伸死載荷p0＞0的作用，則邊界條件為

另外，當球形結構內部含有空穴時，空穴表面無約束的條件為

式（3）、（4）、（5）及邊界條件（6）、（7）組成了不可壓縮超彈性球形結構的外表面在拉伸載荷作用下，球形結構徑向對稱變形的數學模型。

2 問題的求解

由不可壓縮條件λ1λ2λ3=1及式（3）可得

式中，c≥0為待定常數，表示球形結構內半徑的增長量。若c=0，表示變形后球形結構的半徑沒有增長;若c＞0，表示變形后球形結構半徑的增長量為c。

將式（8）代入式（3），可得

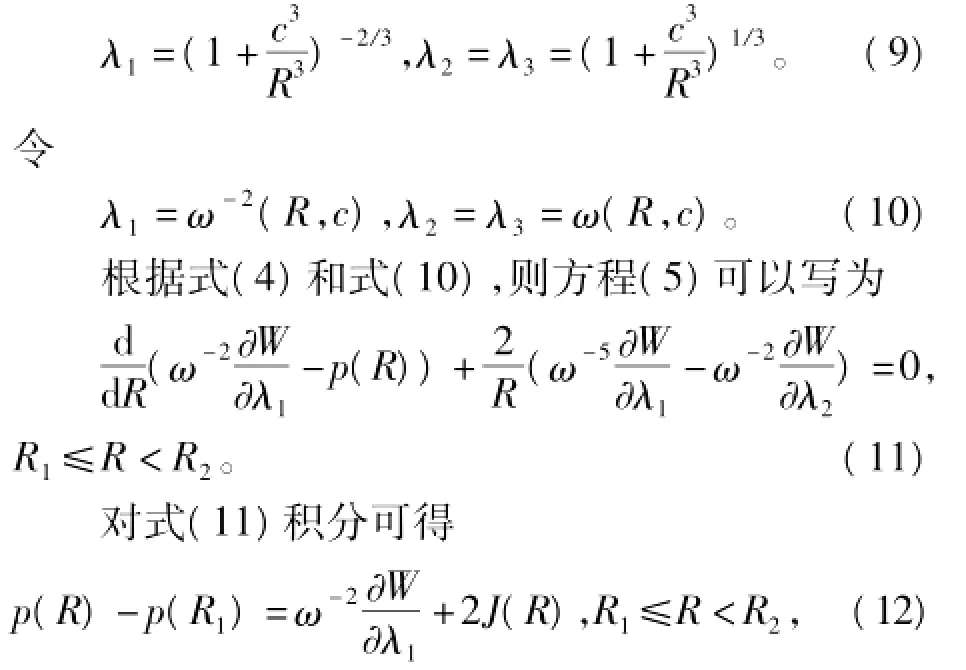
3 幾種球形結構有限變形解的定性分析

3.1 實心球體和含有微孔的球體

假設這兩種球形結構由各向同性不可壓縮Ogden材料組成，其應變能函數為［10］

式中，μ＞0為材料無窮小變形時的剪切模量，α＞0為材料參數。

3.1.1 實心球體

對于實心球體，有R1=0，方程（18）可以寫為

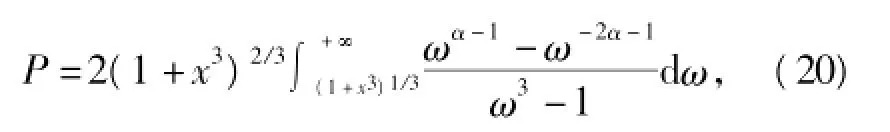
在式（20）中，令x→0+，可得

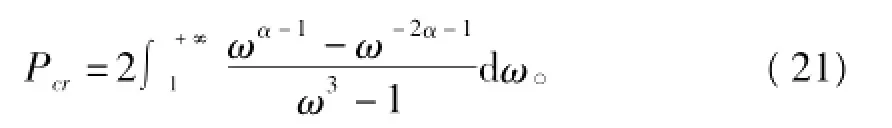
式（21）給出了球體內部有空穴生成時的臨界載荷的表達式。式（21）的右端是一個廣義積分，由此可知臨界載荷Pcr是否有限與材料參數α有著密切的關系。根據廣義積分收斂性的判別法則可知，Pcr收斂當且僅當α＜3。

對于不同的材料參數α，給出了拉伸死載荷P與空穴半徑x之間的關系，如圖1。由圖1可以發現，當α增加時，對應的臨界載荷的值也相應的增加;當拉伸載荷P未達到臨界載荷Pcr之前，無空穴生成;當拉伸載荷P達到或者超過臨界載荷時，有空穴生成，且空穴半徑x隨著拉伸載荷的增加而增加。

圖1 當α取不同值時，P與x的關系曲線

3.1.2 預存微孔

當球形結構為中心含有微孔的球體時，P與d的關系曲線如圖2和圖3（注:d=r（R1）/R2）。

圖2 α=1.5時，P與d的關系曲線

圖3 α=2時，P與d的關系曲線

由此可知，若δ（變形前的微孔半徑與球體外表面半徑之比）很小時，在拉伸載荷P達到某個臨界值之前，微孔幾乎沒有增長;但是當其接近或者超過某個臨界值時，微孔突然快速增長;通過對比圖2和圖3還可以發現，當材料參數α增加時，球體內部微孔發生顯著變化的臨界值也隨著增加。因此，在表面拉伸載荷作用下，球體中微孔的增長受材料參數α和球體內外半徑比值的影響較大。

3.2 球殼和球形薄膜

當球形結構分別為球殼和球形薄膜時，假設球形結構由各向同性不可壓縮的Mooney－Rivlin材料組成，對應的應變能函數為［10］

式中，μ＞0為材料無窮小變形時的剪切模量，β＞0為材料參數。

描述球殼、球形薄膜P與d的關系曲線如圖4和圖5。由此可以看出，對于給定材料參數β，球體的內半徑隨著拉伸載荷P的增加而逐漸增加;δ（球體內半徑與外半徑的比值）越大，內半徑的增長越快。

圖4 表示球殼P與d的關系曲線

圖5 表示球形薄膜P與d的關系曲線

4 結論

本文考慮了各向同性不可壓縮超彈性材料組成的球型結構（實心球體、預存微孔、球殼和球形薄膜）的有限變形問題，利用不可壓縮條件及邊界條件求得了拉伸載荷和內半徑之間的關系，通過對解的定性分析得到了如下結論:

（1）對于各向同性不可壓縮的Ogden材料組成的實心球體，當拉伸載荷P超過臨界載荷Pcr時，球體內部有空穴生成，且空穴半徑x隨著拉伸載荷的增加而逐漸增加;對于由這種材料組成的中心含有微孔的球體，在球體表面拉伸載荷作用下，拉伸載荷P達到某個臨界值之前，微孔幾乎沒有增長;但是當其接近或超過某個臨界值時，微孔突然快速增長，且球體內半徑發生顯著變化，臨界值隨著α的增加而增加，因此，球體中微孔的增長不但與材料參數有關，而且和變形前微孔半徑與球體外半徑的比值有關。

（2）對于各向同性不可壓縮的Mooney－Rivlin材料組成的球殼和球形薄膜，隨著拉伸載荷P的增加，內半徑在逐漸增加;δ越大，內半徑的增長越快。

［1］GENT A N，LINDLEY P B.Internal rupture of bonded rubber cylinders in tension［J］.Proc.R.Soc.Lond.Ser A，1958，249（1257）:289－296.

［2］WILLIAMS M L，SCHAPERY R A.Spherical flaw instability in hydrostatic tension［J］.Int.J.Fractrue Mechanics，1965，1（1）:67－71.

［3］BALL J M.Discontinuous equilibrium solutions and cavitation in nonlinear elasticity［J］.Philos Trans.R.Soc.Lond.Ser.A，1982，306（1496）:557－610.

［4］HORGAN C O，ABEYARATNE R.A bifurcation problem for a compressible nonlinearly elastic medium: growth of micro－void［J］.J.Elasticity，1986，16（2）: 189－308.

［5］SIVALOGANATHAN J.Uniqueness of regular and singular equilibria for spherically symmetric problems of nonlinear elasticity［J］.Arch.Rational.Mech.Anal，1986，96（2）:97－136.

［6］YUAN Xuegang，ZHU Zhengyou，CHENG Changjun.Study on cavitated bifurcation problem for spheres composed of hyper－elastic materials［J］.Journal of Engineering Mathematics，2005，51（1）:15－34.

［7］YUAN Xuegang，ZHANG Hongwu.Effects of constitutive parameters and dynamic tensile loads on radially periodic oscillation of micro－void centered at incompressible hyperelastic spheres［J］.Computer Modeling in Engineering＆Sciences，2009，40（3）:201－224.

［8］任九生，程昌鈞.超彈性材料的不穩定性問題［J］.力學進展，2009，29（5）:566－575.

［9］REN Jiusheng.Dynamics and destruction of internally pressurizedincompressiblehyper－elasticspherical shells［J］.Internation Journal of Engineering Science，2009，47（7－8）:745－753.

［10］OGDEN R W.Large deformation isotropic elasticity:on the correlation of theory and experiment of compressible rubberlike solids［J］.Proc.R.Soc.London，Ser A，1972，328（1575）:567－583.

Radial Finite Deformation of Incompressible Hyperelastic Spherical Structures

YUAN Xue－gang1，DU Yan－fang2，WEN Yao1
（1.College of Science，Dalian Nationalities University，Dalian Liaoning 116605，China; 2.School of Mathematics，Liaoning Normal University，Dalian Liaoning 116029，China）

In this paper，the radial finite deformation problems are examined for spherical structures composed of isotropic incompressible hyperelastic material under tensile loads on their outer－surfaces.First of all，an exact relation between tensile load and inner radius of spherical structure is obtained by the incompressibility condition and the boundary conditions.Secondly，qualitative analyses are performed for solutions describing the finite deformation of the four spherical structures（i.e.，solid sphere，sphere with an initial micro-void，spherical shell，spherical membrane）.Finally，the effects of material parameters and structure parameters on radial deformation of spherical structures are discussed in detail by utilizing numerical examples.

incompressible hyperelastic material;spherical structure;finite deformation;qualitative analysis

1009－315X（2012）01－0033－04

2011－05－25

國家自然科學基金面上項目（10872045）;教育部新世紀優秀人才支持計劃（CNET－09－096）;中央高校基本科研業務費專項資金資助項目（DC10030104）。

袁學剛（1971－），男，吉林樺甸人，教授，博士，學校優秀學術帶頭人，碩士生導師，主要從事非線性彈性材料和結構的有限變形問題研究。

O343

A超彈性材料中固有的非線性現象。近幾年來，對于超彈性材料組成的球形結構的研究已經相當深入，如實心球體的空穴現象、球殼的膨脹、柱體的翻轉和彎曲等等。其中，文獻［6－7］研究了橫觀各向同性不可壓縮的非線性彈性材料中空穴的靜、動態生成以及預存微孔的增長及振動問題;文獻［8］綜合近年來的研究成果，對超彈性材料中的材料不穩定性問題的研究成果和最新進展進行了系統的評述，并且闡述了由Rivlin材料組成的各種球形結構的不穩定性問題的特點、問題的求解以及主要的結果;文獻［9］研究了周期或者恒定內壓作用下不可壓縮neo－hookean材料組成的球殼的動力響應和破壞機理的問題。

（責任編輯 鄒永紅）