海上攝像平臺運動對目標在靶面成像位置影響的分析

鄧江生，樊利恒，古立莉

（1.海軍航空儀器計量站 上海 200436；2.海軍航空工程學院 控制工程系，山東 煙臺 264001；3.中國人民解放軍94748部隊 江蘇 南京 210008）

攝像平臺的運動避免不了的對目標成像位置產生影響[1]。海上攝像平臺的運動主要有四種形式：橫搖、縱搖、艏搖和垂蕩[2]。目前的研究都集中在平臺的穩定性分析和怎樣進行補償上，而關于平臺運動對攝像系統影響的分析幾乎無人提及[3-7]。通過運動對成像位置的影響分析不僅為平臺穩定裝置提供了性能指標的基礎，該工作是一項非常有意義和重要的工作。下面對這些運動對成像位置的影響一一加以分析并針對可見光波段和紅外波段兩種情況進行具體計算。

由于目標成像在靶面中間位置是最理想的位置，也是最易受平臺運動影響的位置，如果在中心位置成像的情況下平臺運動使目標移出視場，則在其他成像位置時也必然移出視場。本文分析假設目標成像在靶面中心，然后分析攝像平臺運動對目標成像位置的影響進行定量計算和定性分析。

1 各種運動對成像位置的影響

1.1 橫搖對成像位置的影響

分析橫搖對成像的影響。橫搖使得攝像機在水平和垂直方向上有個位移 （x，y）（如果攝像機與橫搖在橫搖軸上方并且距離為h米，建立以攝像機為原點的直角坐標系，則|x|=h×sinα，|y|=h（1-|cosα|），同時攝像機成像面有一個相對于它自身中心的旋轉，旋轉角度為α。設平臺靜止時目標在靶面的成像位置為（xt，yt），目標距離攝像機的距離為 d，則位移造成的目標成像位置位移為

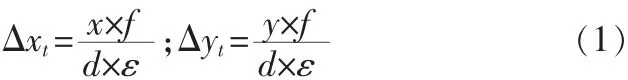
其中f為焦距，α為橫搖的角度，ε為像元尺寸。

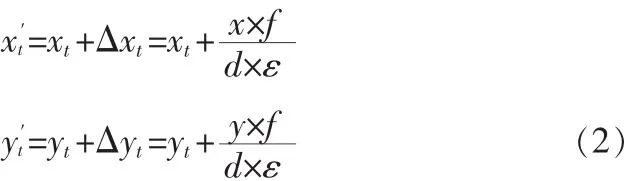
考慮旋轉對成像位置造成的影響。將初始位置（xt，yt）用極坐標表示，可得到目標的位置為（r，θ），其中：

把橫搖角度α考慮進去，可求得平臺橫搖對目標成像位置的綜合影響，得到發生橫搖時目標成像位置的極坐標表示為：（r′，θ′）

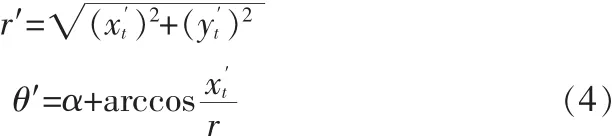
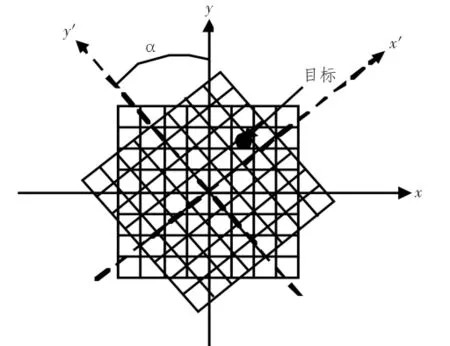
圖1 旋轉對成像位置的影響Fig.1 Rotation’s impact on the location of imagery

1.2 縱搖對成像位置的影響

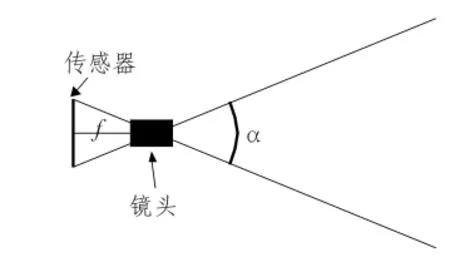
圖2 視場角Fig.2 Angle of FOV（field of view）

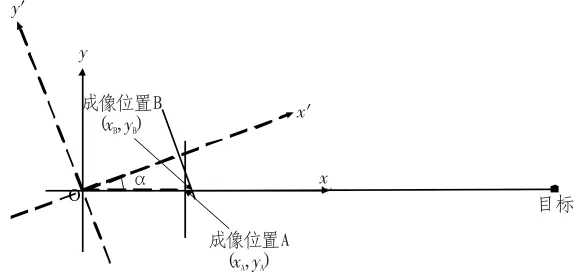
圖3 縱搖對成像位置影響的示意圖Fig.3 Pitching’s impact on the location of imagery

分析縱搖對成像的影響。如圖3所示，當縱搖的幅度為α且初始位置為靶面中心時，則縱搖角β對成像位置的影響如公式（6）所示：

其中，Yn縱搖幅值對成像面在垂直方向的影響，表現為目標在CCD靶面位移的行數，ε為像元尺寸。

1.3 艏搖對成像位置的影響

艏搖對成像位置的與縱搖的情況類似，不同的只是方向不同。設縱搖的角度為β，則艏搖角β對成像位置的影響如公式（7）所示：

其中，Xn縱搖幅值對成像面在垂直方向的影響，表現為目標在CCD靶面位移的行數，f為焦距，ε為像元尺寸。

1.4 垂蕩對成像位置的影響

分析垂蕩對成像的影響。垂蕩使得攝像機在垂直方向上有個位移Δy，在水平方向上對平臺沒有影響。設平臺靜止時目標在靶面的成像位置為（xi，yi），目標距離攝像機的距離為d，則位移造成的目標成像位置位移為：

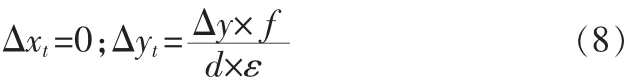
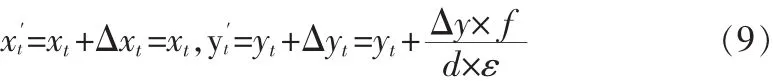
2 各種運動對可見光波段相機成像的影響

選用的可見光波段相機為Adimec-RAAdimec-RA-4020，該相機的像素數為1 728×1 296，像元尺寸為7.4μm×7.4μm，焦距為 75 mm，視場角為 9.7°×7.3°（水平×垂直）。

2.1 橫搖的影響

由公式（3）和公式（4）可以看出，平臺靜止時目標的成像位置對最終成像位置的影響很大。如圖4所示，考慮只有旋轉的情況，此時只要目標成像在圖4中圓形區域內目標就不會出視場，而當目標成像在圓形區域外時只要旋轉一定角度則目標就出移出視場，特殊情況是成像在x軸與靶面交界處，此時只要發生旋轉目標就會移出視場。目標與靶面中心的距離越大則受旋轉的影響越大。可以計算出圖4圓的半徑Y為r=648，其中r的單位為像素的行數。如果r＞648但成像位置與x軸夾角小于橫搖角時目標也不會出視場，即 θ=arctan（x/y）<α。

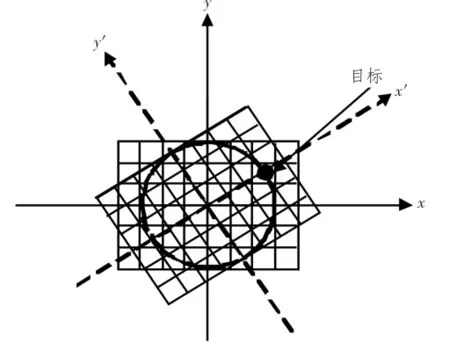
圖4 只有旋轉沒有位移的情況Fig.4 Rotation without displacement in any direction

2.2 縱搖的影響

分析平臺靜止時目標在靶面中心成像的情況，則當目標移動像素數的一半時目標移出視場，根據公式（6）計算目標移出視場時的縱搖角。將代入可以求得α=3.658 3°。即當縱搖角大于臨界α臨界時目標會出視場，而當搖擺角α小于α臨界時，目標只要成像在中心7.3°～2α區域就不會移出視場。

2.3 艏搖的影響

分析平臺靜止時目標在靶面中心成像的情況，則當目標移動像素數的一半時目標移出視場，根據公式（7）計算目標移出視場時的艏搖角。將f=75 mm，ε=7.4μm，864代入可以求得β=4.872 6°。即當艏搖角臨界大于β臨界時目標會出視場，而當搖擺角β小于β臨界時，目標只要成像在中心7.3°～2β區域就不會移出視場。

2.4 垂蕩的影響

分析垂蕩對可見光波段相機成像的影響。設垂蕩的幅度為Δy，設平臺靜止時目標在靶面的成像位置為（0，0），目標距離攝像機的距離為d=6 km，ε=30μm，f=75 mm，則位移造成的目標成像位置位移為：

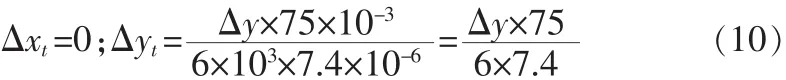
當Δyt=648時目標才會出視場，此時Δy=383.616 m，即垂蕩為383.616 m時目標移出視場。

根據上面的敘述和計算，得出表1結論。

表1 使得目標不移出視場的平臺運動范圍Tab.1 Range of platform’s movement when target in the FOV

3 各種運動對紅外波段相機成像的影響

選用的紅外波段相機為GUIDIR公司的IR600紅外熱像儀，該相機的像素數為 320×256，像元尺寸為 30μm×30μm，焦距為 600 mm/150 mm/22 mm，相應的視場角為 0.92°×0.73°/3.67°×2.93°/24.62°×19.80°（水平×垂直）。

3.1 橫搖的影響

由公式（3）和公式（4）可以看出，平臺靜止時目標的成像位置對最終成像位置的影響很大。如圖4所示，考慮只有旋轉的情況，此時只要目標成像在圖4中圓形區域內目標就不會出視場，而當目標成像在圓形區域外時只要旋轉一定角度則目標就出移出視場，特殊情況是成像在x軸與靶面交界處，此時只要發生旋轉目標就會移出視場。目標與靶面中心的距離越大則受旋轉的影響越大。可以計算出圖4圓的半徑r為r=128，其中r的單位為像素的行數。如果r＞648但成像位置與x軸夾角小于橫搖角時目標也不會出視場，即θ=arctan（x/y）＜α。

3.2 縱搖的影響

分析平臺靜止時目標在靶面中心成像的情況，則當目標移動像素數的一半時目標移出視場，根據公式（6）計算目標移出視場時的縱搖角。將ε=30 mm，f=600 mm/150 mm/22 mm，Yn=256/2=128 代入 Yn=f×tanα/ε， 可以求得 α臨界=0.3667°/1.4665°/9.9010°。即當縱搖角大于 α臨界時目標會出視場，而當搖擺角 α小于 α臨界時，目標只要成像在中心 0.73°-2α/2.93°－2α/19.80°－2α 區域就不會移出視場。

3.3 艏搖的影響

分析平臺靜止時目標在靶面中心成像的情況，則當目標移動像素數的一半時目標移出視場，根據公式（7）計算目標移出視場時的艏搖角。將ε=30 mm，f=600 mm/150 mm/22 mm，Xn=320/2=160 代入 Xn=f×tan β/ε， 可以求得 β臨界=0.458 4°/1.832 8°/12.308 0°。即當艏搖角大于 β臨界時目標會出視場，而當搖擺角β小于 β臨界時，目標只要成像在中心0.92°-2β/3.67°－2β/24.62°－2β 區域就不會移出視場。

3.4 垂蕩的影響

分析垂蕩對可見光波段相機成像的影響。設垂蕩的幅度為Δy，設平臺靜止時目標在靶面的成像位置為（0，0），目標距離攝像機的距離為d=6 km，焦距為f=600 mm/150 mm/22 mm，ε=30μm，則位移造成的目標成像位置位移為

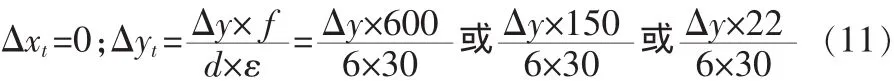
當Δyt=128時目標才會出視場，此時Δy=38.4 m或153.6 m或1 047.273 m，即垂蕩為Δy=38.4 m或153.6 m或1 047.273 m時目標移出視場。

根據上面的敘述和計算，得出如表2～4結論。

表2 使得目標不移出視場的平臺運動范圍（f=600 mm）Tab.2 Range of platform’s movement when target in the FOV（f=600 mm）

表3 使得目標不移出視場的平臺運動范圍（f=150 mm）Tab.3 Range of platform’s movement when target in the FOV（f=150 mm）

表4 使得目標不移出視場的平臺運動范圍（f=22 mm）Tab.4 Range of platform’s movement when target in the FOV（f=22 mm）

4 結 論

由上述分析可以看出，平臺的垂蕩運動對目標成像位置的影響最小；橫搖對成像位置的相應與目標在靶面的最初成像位置有關；縱搖和艏搖對成像位置的影響最大，與傳感器尺寸、焦距有關，目標出不出視場由搖擺角與視場角確定。根據分實際情況，在惡劣海況下目標是比較容易出視場的，所以必須加裝穩定裝置。

[1]溫昌禮.平臺角振動對圖像測量系統的影響 [D].長沙:國防科技大學，2006.

[2]李偉.船舶液壓穩定平臺的設計與分析[D].大連:大連海事大學，2010.

[3]孫輝，郎小龍，李志強，等.動載體光電平臺視軸穩定精度的檢測[J].光學精密工程，2011，19（9）:2131-2138.SUN Hui，LANG Xiao-long，LI Zhi-qiang，et al.Measurement for LOS stabilization accuracy of electro-optical imaging systemon moving carrier[J].Optics and Precision Engineering，2011，19（9）:2131-2138.

[4]毛峽，劉言，梁曉庚.極坐標框架兩軸平臺光軸穩定算法[J].兵工學報，2011，32（10）:1260-1265.MAO Xia，LIU Yan，LIANG Xiao-gen.Algorithm of optical axis stabilization based on two-axis polar coordinate frame platform[J].Acta Armamentarii，2011，32（10）:1260-1265.

[5]王晨，馬彩文，梁雁冰，等.基于機動平臺的光電經緯儀自穩定跟蹤技術[J].紅外與激光工程，2010，39（4）:644-670.WANG Chen，MA Cai-wen，LIANG Yan-bin，et al.Selfstabilization target tracking technology based on mobile platform [J].Infrared and Laser Engineering，2010，39 （4）:644-670.

[6]夏靜萍，王道波.四框架穩定跟蹤平臺原理樣機設計與實現[J].兵工自動化，2012，31（1）:86-90.XIA Jing-ping，WANG Dao-bo.Design and realization of four-gimbal stabilization and tracking platform prototype[J].Ordnance Industry Automation，2012，31（1）:86-90.

[7]周小剛，汪立新，余嬙，等.光纖陀螺平臺穩定回路設計與實驗研究[J].宇航學報，2008，29（2）:567-575.ZHOU Xiao-gang，WANG Li-xin，SHE Qiang，et al.Designs of the servo loop of optic fiber gyroscope platform and experiment research[J].Journal of Astronautics，2008，29（2）:567-575.