擬小波方法在梁動力穩定性分析中的應用

宋志偉， 李 威， 渠鴻飛

(華中科技大學 船舶與海洋工程學院， 湖北 武漢 430074)

結構的動力穩定性一直受到人們廣泛的關注[1～5]。解析法[1]和數值方法[2～4]已經被成功應用于結構動力穩定性分析中。本文提出了求解梁動力穩定性的擬小波方法[6]，利用該方法計算了兩端簡支和固支梁的動力失穩區，并討論了周期性軸向力中恒定項對動力失穩區的影響，與解析解對比驗證了采用擬小波法求解梁動力穩定性的可行性和有效性。

1 振動方程

當直梁受到周期性軸向力PS+PDcos(θt)作用時，根據歐拉梁理論，忽略轉動慣量和剪切效應，其振動方程為[1]：

(1)

其中,E為楊氏模量,I為截面慣性矩,m為單位長度質量,PS+PDcos(θt)為周期性軸向力，PS為恒定項,PD和θ分別為幅值和激勵圓頻率，u為橫向位移,t為時間。

為了簡化，引入以下無量綱量

則,(1)式可以化為:

(2)

將(2)式改寫為:

(3)

兩端簡支邊界條件為:

U(0,τ)=U(1,τ)=0，

兩端固支邊界條件為:

U(0,τ)=U(1,τ)=0，

2 數值方法和離散式子

2.1 擬小波數值方法

擬小波方法是Wei[6]等人提出來的一種新型的數值方法，已經被成功應用于科學和工程多領域中[7～10]。關于該方法的數學理論和應用，可參考Wei等[8～10]的文獻。根據Shannom定理,引進擬尺度函數[7]

δΔ,σ(x-xk)=

(4)

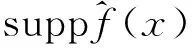
(5)

由于擬小波具有良好的局域特性,實際計算只需要在網格點x附近取2W個計算點即可達到計算精度。(5)式對空間坐標x的n階導數為

(n=0,1,2, …)

(6)

在(1)式中需要求空間的二階和四階導數，其表達式見文獻[8]。

2.2 離散式子

本文利用擬小波數值離散格式(6)式離散(3)式的空間導數, 四階Runge - Kutta (RK4)法離散時間導數。具體如下[7]: 將空間X坐標進行均勻等分,單元網格大小記為ΔX=(1-0)/N(N為單元網格總數)。網格點坐標Xj(j=1,2,…,N+1),于是Xj-Xj+k=-kΔX,在網格點Xj的無量綱位移U記為Uj, 則(3)式可以寫為：

(j=1,2,…,N+1)

(7)

令 {yj}={y1,y2,…,y2N+2}={U1,U2,…,UN+1,V1,V2,…,VN+1} (j=1,2,…,2N+2)

當j=1,2,…,N+1時

fj=yj+N+1

(8)

當j=N+2,N+3,…,2N+2 時

(9)

則可以得到統一寫成的半離散的形式

(10)

用四階Runge - Kutta (RK4)法離散時間導數，其格式[11]為：

(11)

(j=N+2,N+3,…,2N+2)

(12)

(j=N+2,N+3,…,2N+2)

(13)

3 算例與討論

3.1 梁的動力穩定性

首先討論兩端簡支和固支梁受到軸向力PDcos(θt)作用時梁的動力穩定性。此時恒定項PS=0，即(3)式中α=0。為了計算梁的第一失穩區[1],Θ的取值為[1.5, 2.5]，μ的取值為[0，0.5]。計算時，μ由穩定區取值到失穩區，間距為0.025。依據動力失穩準則[3]：如果振動的幅值在很長一段時間內單調遞增,則認為振動是不穩定的；否則,振動是穩定的。判斷出振動響應的穩定性，從而得到梁的失穩區。對于簡支梁，初始條件和參數設置為U(X,0)=0,?U(iΔX,0)/?τ=sin(iΔXπ)(i= 0,1,2,…,N)。λl=π,N=18,W=15,r=2.5,Δτ= 2.5×10-6。對于固支梁，初始條件和參數設置為：U(X,0)=0,?U(X,0)/?τ=[0 0.0325 0.1191 0.2435 0.3900 0.5435 0.6901 0.8178 0.9164 0.9787 1.0000 0.9787 0.9164 0.8178 0.6901 0.5435 0.3900 0.2435 0.1191 0.0325 0]，λl=4.7300,N=20,W=15,r=2.5,Δτ=2.5×10-6, 參數N，W，r的設置參考文獻[8，9，12]。

圖1為簡支梁自由振動位移響應曲線。從圖中發現由擬小波法計算的中點位移響應曲線和不同無量綱時間點的變形曲線分別與解析解吻合得很好。這說明采用擬小波法計算梁的動力響應是可行的和有效的。同時，由擬小波法計算的不同時間點的變形曲線是光順的，這說明采用反對稱延拓[9]處理簡支邊界是合理的。

圖1 簡支梁自由振動位移響應曲線

圖2 簡支梁無量綱位移響應曲線

圖2為簡支梁無量綱位移響應曲線。由圖2(a)、(b)和(e)可以判斷這些曲線是隨時間單調遞增的, 則在這些情況下振動是不穩定的；由圖2(c)和(d)可以判斷這些振動是穩定的。 由圖2(c)、(d)和(e)可得到，當θ/2Ω不變時，隨著μ增大，梁由穩定狀態逐步變為失穩狀態[1]。 重復上述過程，可以得到不同θ/2Ω和μ所對應的位移響應曲線以及其穩定性。圖3為簡支梁的穩定圖，在圖3中,由“●”和“○”分別形成的穩定區和不穩定區,與理論的穩定和不穩定區[1]吻合得很好。

“—”為理論失穩邊界；“●”,“○”為擬小波法穩定和失穩結果圖3 簡支梁穩定圖

上述梁的動力穩定性是根據位移響應曲線來判斷的,也可以根據相位圖來判斷穩定性[13]。圖4為簡支梁的相位圖。其中，橫軸和縱軸分別為中點無量綱位移U(0.5,τ)和速度V(0.5,τ)，相軌跡是順時針方向，點’S’和’E’分別表示計算時間起點和終點。由圖4可以判斷出θ/2Ω=0.9,μ=0.15和μ=0.175時振動是穩定的；θ/2Ω=0.9,μ=0.2時振動是不穩定的。這些結論與前面的結論相同。

圖4 簡支梁的相位圖

利用上述擬小波算法，采用對稱延拓[9]處理邊界條件，可以得到兩端固支梁的穩定圖見圖5。在圖5中,由‘●’和‘○’分別形成的穩定區和不穩定區,與理論的穩定和不穩定區[1]吻合得很好。

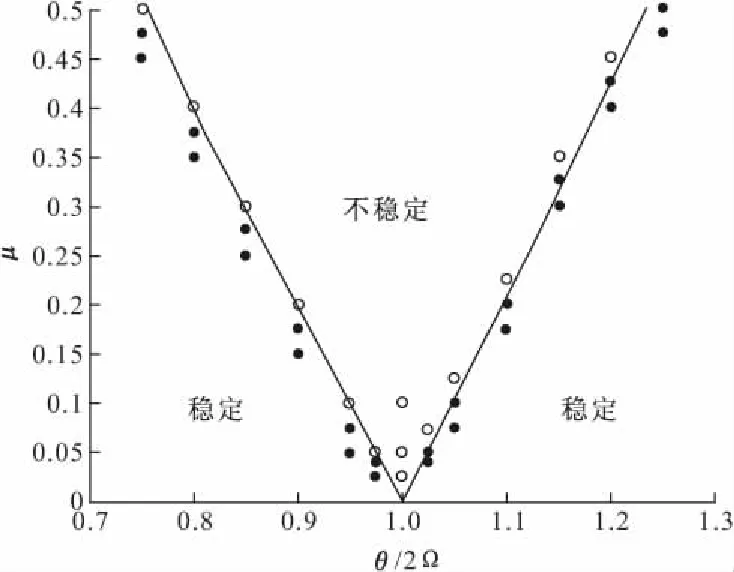
“—”為理論失穩邊界；“●”,“○”為擬小波法穩定和失穩結果圖5 固支梁的穩定圖

3.2 恒定項的影響

本小節討論兩端簡支梁受到軸向力作用時恒

定項對失穩區的影響。分別取α=0.3和α=0.5來討論，相關參數和初始條件的設置與計算簡支梁穩定性時相同。

圖6為α=0.3時梁中點無量綱位移U(0.5,τ)響應曲線。 由圖6(a)、(d)和(f)，可以判斷α=0.3時θ/2Ω=0.837,μ=0.05；θ/2Ω=0.753,μ=0.2；θ/2Ω=0.962,μ=0.325情況下振動是不穩定的；由圖6(b)、(c)和(e)可以判斷α=0.3時θ/2Ω=0.753,μ=0.15；θ/2Ω=0.753,μ=0.175；θ/2Ω=0.962,μ=0.3情況下振動是穩定的。重復上述過程，即可得到α=0.3時梁的穩定圖，采用同樣的方法可以得到α=0.5時梁的穩定圖見圖7。在圖7中由擬小波法得到α=0.3和α=0.5時的不穩定區和穩定區與理論的不穩定區和穩定[1]區吻合很好；同時發現隨著軸向力中恒定項的增大(α由0.3增大到0.5)，失穩區由高頻區移到低頻區，結構對周期性軸向力變得敏感，這與理論規律[1]也是相同的。

圖6 α=0.3時梁的無量綱位移響應曲線

“—”,“- -”,“- · -”為α=0, α=0.3, α=0.5理論失穩邊界；“●”,“○”為α=0.3擬小波法穩定和失穩結果；“▼”,“▽”為α=0.5擬小波法穩定和失穩結果圖7 變化時梁的穩定圖

4 結 語

本文采用擬小波方法研究了兩端簡支和兩端固支梁的動力穩定性，還討論了軸向力中恒定項對穩定區的影響.通過對比分析，發現由擬小波法所得的穩定圖與理論的穩定圖吻合得很好，同時研究表明軸向力中恒定項的增加導致失穩區由高頻區移向低頻區,這與理論結果也是相同的。從而說明采用擬小波法研究梁的動力穩定性是可行的和有效的。本文的研究也為結構動力穩定性分析提供了一種新的思路和方法。

[1] 符·華·鮑洛金.彈性體系的動力穩定性[M].林硯田，譯.北京:高等教育出版社,1960.

[2] Iwatsubo T, Sugiyama Y, Ishihara K. Stability and non-stationary vibration of columns under periodic loads[J]. Journal of Sound and Vibration, 1972, 23(2): 245-257.

[3] Briseghella L, Majorana C E, Pellegrino C. Dynamic stability of elastic structures: a finite element approach[J]. Computers and Structures, 1998, 69(1): 11-25.

[4] Svensson I. Dynamic stability regions in a damped system[J]. Journal of Sound and Vibration, 2001, 244(5): 779-793.

[5] Chiba M. Influence of horizontal excitations on dynamic stability of a slender beam under vertical excitation[J]. Experimental Mechanics, 2009, 49(5): 541-549.

[6] Wei G W. Discrete singular convolution for the solution of the Fokker-Planck equations[J]. Journal of Chemical Physics, 1999, 110(18): 8930-8942.

[7] Wan D C, Wei G W. The Study of quasi -wavelets based numerical method applied to Burgers’ equations[J]. Applied Mathematics and Mechanics (English Edition), 2000, 21(10): 1099-1110.

[8] Wei G W. Discrete singular convolution for beam analysis[J]. Engineering Structures, 2001, 23(9): 1045-1053.

[9] Wei G W, Zhao Y B, Xiang Y. Discrete singular convolution and its application to the analysis of plates with internal supports. Part 1: theory and algorithm[J]. International Journal for Numerical Methods in Engineering, 2002, 55(8): 913-946.

[10] Zhao S, Wei G W, Xiang Y. DSC analysis of free -edged beams by an iteratively matched boundary method[J]. Journal of Sound and Vibration, 2005, 284(1-2): 487-493.

[11] 王能超.數值分析簡明教程(第二版)[M].北京:高等教育出版社,2003.

[12] Xiong W, Zhao Y B, Gu Y. Parameter optimizatim in the regularized Shannon’s kernels of higher-order discrete singular convolutions[J]. Communications in Numerical Methods in Engineering, 2003,19: 377-386.

[13] 劉延柱,陳立群.非線性振動[M].北京:高等教育出版社,2001.