混凝土橋塔溫度場的時變分析及溫度梯度模式研究

任 翔

(西安科技大學建筑與土木工程學院,西安 710054)

混凝土橋塔等薄壁箱形結構在日照作用下截面長寬方向和厚度方向易產生較大的非線性溫差,這種日照非線性溫差荷載產生的溫度應力也是導致這類結構開裂的重要因素之一[1-8]。目前,國內外對混凝土橋梁結構溫度場的研究頗多,但主要集中于上部混凝土箱梁結構。文獻[1]對混凝土箱梁溫度分布進行了一系列的實驗研究,認為日照最大溫差和基準溫度是橋梁設計的必要參數,文獻[2]對加拿大The Muskwa River組合箱梁橋進行了溫度場現場測試,并對板梁斷面、單箱斷面和雙箱單室斷面的溫度分布的影響因素進行了分析,文獻[3]長期對韓國漢城某公路混凝土-鋼箱梁結合梁橋溫度場進行連續觀測,文獻[4]，[5]在南京長江二橋北漢橋施工過程中,測試了箱梁溫度場,并分析了箱梁的溫度場分布。文獻[6]在荊州長江公路大橋500 m斜拉橋主梁上進行了溫度觀測,并根據實測溫度觀測結果提出了一種溫度場的數值計算方法。混凝土橋墩溫度場觀測方面始于20世紀60年代中期,鐵道部大橋工程局、鐵道部第四勘測設計院和鐵道科學研究院西南研究所對實體橋墩、薄壁空心墩和拼裝式箱形橋墩進行了溫度場現場觀測[7]。而對下部結構溫度場及溫度場分布模式的研究很少,諸如：斜拉橋和懸索橋大體積混凝土橋塔等。因此,依托背景橋梁,對混凝土橋塔日照溫度場進行了觀測,分析了混凝土橋塔結構的溫度場隨時間的變化特征和規律,進一步研究了混凝土橋塔箱形結構溫度梯度模式。研究結論可為混凝土橋塔等薄壁箱形結構的設計和編制相關規范提供參考。

1 溫度場觀測時間和測點位置

1.1 測試時間

分別選取了氣候寒冷的1月份、天氣溫和的4月份和天氣炎熱的8月份等3個典型的季節進行了混凝土橋塔溫度場測試,每個季節連續數天進行測試,每天的測試頻率為每間隔2 h測試1次。每個季節選擇2 d的測試數據作為橋塔溫度場變化規律的分析值。

1.2 測試斷面布置

圖1給出了某雙塔單跨鋼箱梁懸索橋混凝土空心箱形橋塔結構的溫度場測試斷面和測點布置。橋塔溫度測試斷面選在距橋面以上1 m處,每個塔壁內、外側表面分別設置5個測點。

圖1 橋塔溫度測試斷面及測點布置(單位：m)

圖1中：“1～4”表示4個塔壁的外表面；“1′～4′”表示4個塔壁內表面。

2 日照溫度場隨時間的變化規律

2.1 橋塔內外環境溫度

橋塔內外環境溫度在3個季節下的變化情況見圖2。圖中水平軸為溫度測試時刻,0時刻為溫度場測試日的上午6時,豎軸表示不同測試時刻對應的塔內外環境溫度值。

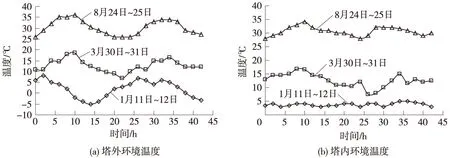
圖2 3個季節下塔內外環境溫度隨時間的變化

圖3 1月11日～12日塔壁內外表面溫度隨時間的變化

由圖2可以看出,3個季節下,塔外環境溫度隨時間近似呈正弦曲線變化,而塔內環境溫度變化比較平緩,明顯沒有塔外環境溫度變化大。1月11日～12日2 d內,上午8時左右塔外溫度達到最高,凌晨4時左右溫度到達最低點,塔外日最大環境溫差為12 ℃,而塔內日最大環境溫差為2 ℃；3月30日～31日2 d內,下午14時至16時期間塔外溫度達到峰值,凌晨4時左右溫度達到最低,塔外日最大環境溫差為13.5 ℃,而塔內日最大環境溫差為7.8 ℃；8月24日～25日2 d內,塔外環境溫度到下午16時達到峰值,其后溫度開始下降,最低溫度約在凌晨4時左右,塔外日最大環境溫差為9.0 ℃,而塔內日最大環境溫差為5 ℃。

2.2 橋塔塔壁表面溫度場

圖3～圖5示出了3個季節下,塔壁內外表面溫度隨時間的變化。圖中水平軸為溫度測試時刻,0時刻為溫度場測試日的上午6時,豎軸表示不同測試時刻對應的塔壁內外表面溫度值。

圖4 3月30日～31日塔壁內外表面溫度隨時間的變化

圖5 8月24日～25日塔壁內外表面溫度隨時間的變化

由圖3～圖5顯示,3個季節下,塔外表面溫度變化比較相似,均近似呈正弦曲線變化的趨勢。1月11日～12日2 d內,塔外1號面和2號面高溫時刻是上午8時,4號面高溫時刻出現在下午14時,3號面溫度變化不明顯。主要是由于各個塔壁受太陽照射的時刻不同所導致。1～4號面最大日較溫差依次為9.6、9.5、6.6 ℃和8.5 ℃；3月30日～31日2 d內,塔外1-4號面2 d內表面高溫時刻均出現在下午14時左右,低溫時刻出現凌晨4左右,最大日較溫差依次為12.9、9.9、9.4 ℃和15.0 ℃；8月24日～25日2 d內,塔外1～4號面高溫時刻均出現在下午14時左右,低溫時刻出現凌晨4左右,最大日較溫差依次為12、10.4、9 ℃和12 ℃。由于受日照的影響,1號面和4號面的溫度明顯高于2號面和3號面的溫度值。3個季節下,塔內1′～4′號面溫度變化趨勢相近,但變化不明顯,最大日較溫差均未超過5.0 ℃。

2.3 塔壁截面厚度方向的溫差

圖6～圖8所示的是3個季節下,塔壁內外表面壁厚方向的溫差值。圖中水平軸為溫度測試時刻,0時刻為測試日上午6：00,圖中各個時刻對應的數值為外表面和內表面溫差值。

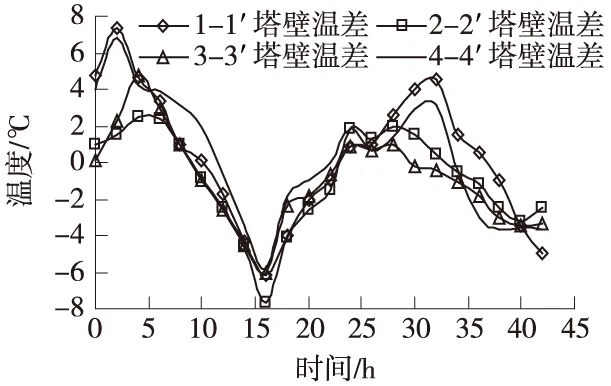
圖6 1月11日～12日塔壁內外表面溫差隨時間的變化

圖8 8月24日～25日塔壁內外表面溫差隨時間的變化

由圖6～圖8可以看出,3個季節下,塔壁內外表面溫差在2 d內隨時間均近似呈正弦曲線變化。1月11日～12日2 d內,各個測試面的最大正溫差發生在上午8時左右,東、北、西和南4個塔壁內外表面最大正溫差分別為7.5、2.5、4.8 ℃和6.8 ℃；最大負溫差發生在晚上22時左右,其值分別為-6.2、-7.5、-6.1 ℃和-5.8 ℃。3月30日～31日2 d內,各個測試面的最大正溫差均發生在下午14時左右,東、北、西和南4個塔壁內外表面最大正溫差分別為6.6、2.0、2.5 ℃和9.3 ℃；最大負溫差分別發生在凌晨4時左右,其值分別為-6.0、-6.8、-6.5 ℃和-5.9 ℃。8月24日～25日2 d內,各個測試面的最大正溫差發生在下午14時到16時這個時間段,東、北、西和南4個塔壁內外表面最大正溫差均為8、6.2、6.5 ℃和8 ℃；最大負溫差分別發生在凌晨4時到6時；其值分別為-2、-1.5、-1.5 ℃和-1.5 ℃。

2.4 塔壁截面長寬和寬度方向的溫差

圖9～圖10分別示出了橋塔截面沿長寬方向2個外表面和寬度方向兩個外表面的溫差隨時間的變化。圖中水平軸為溫度測試時刻,0時刻為測試日上午6時,圖中各個時刻對應的數值為橋塔截面長寬方向2個對立外表面的溫差值。

圖9 橋塔橫橋向兩外表面溫差隨時間的變化

圖10 橋塔順橋向兩外表面溫差隨時間的變化

由圖9～圖10可以看出,1月11日～12日2 d內,橋塔橫橋向兩外表面的最大溫差發生在上午8時左右,最大溫差為6.2 ℃；橋塔順橋向兩外表面的最大溫差也發生在上午8時左右,最大溫差4.1 ℃；3月30日～31日2 d內,橋塔橫橋向2個塔壁外表面的最大溫差發生在下午14時左右,最大溫差為5.4 ℃,溫差較大的時段主要集中在下午14時到晚上20時,夜間到上午10時這一時段溫差較小,變化也均衡；橋塔截面寬度方向兩個塔壁的外表面的最大溫差發生在下午4時左右,最大溫差為9.2 ℃,溫度差較大的時段主要集中在下午14時到16時,其余時段溫差比較小；8月24日～25日2 d內,橋塔橫橋向兩外表面的最大溫差發生在下午14時左右,最大溫差為5.0 ℃,溫度差較大的時段主要集中在下午14時到16時,夜間20時到次日上午8時這一時段溫差較小,變化均衡；橋塔順橋方向2個外表面的最大溫差發生在下午4時左右,最大溫差為5.9 ℃,溫度差較大的時段主要集中在下午14時到16時,其余時段溫差比較小。橋塔壁厚方向有最大正向溫差時,橋塔截面長寬方向兩對立面外表面溫差同時也分別有最大正向溫差值。

3 溫度梯度分布模式

3.1 溫度場分布的有限元計算法

瞬態溫度場不僅是空間域上Ω的函數,也是時間域t上的函數,二者并不耦合,因此可以采用部分離散的方法[9]。

混凝土熱傳導公式可由下列二維偏微分方程表示[10]

(1)

式中：x,y為笛卡爾坐標；T為溫度場分布；k為熱傳導系數；c,ρ分別為比熱容和密度。

邊界條件反映物體介質表面與其周圍環境之間的熱交換關系。常見邊界條件可分為3類。

第一類邊界條件是指已知物體邊界上的溫度,即

T|Γ=T|Γ(t)

(2)

式中：Γ表示物體的邊界。

第二類邊界條件是已知物體邊界上的熱流密度,即

(3)

式中：kn為邊界平面外法線方向的熱傳導系數；q(t)為由外界流入物體內部的熱流密度。

第三類邊界條件是已知與物體接觸的流體介質的溫度和換熱系數,即

(4)

式中：h為換熱系數；Ta(t)為流體介質的溫度。

首先將空間域Ω離散為有限個單元體,構造單元內的溫度函數T,由結點溫度差值得到,溫度函數φ如下

(5)

差值函數Ni僅為空間函數,同時也具有差值函數的基本性質。式(5)滿足邊界條件,并代入式(1)得

(6)

將式(6)代入邊界條件式(3)和式(4)得

(7)

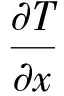
(8)

令余量的加權積分為零,即

(9)

式中,ω1,ω2,ω3為權函數,ω1=Nj,ω2=ω3=Nj,j=1,2,K,ne。

將ω1,ω2,ω3代入式(9)中,積分得到矩陣方程

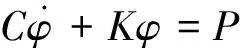
(10)

(11)

3.2 有限元計算模型

采用ANSYS10.0的熱分析功能,來計算橋塔的溫度場分布及其變化情況。選取距橋面以上1 m處橋塔截面的幾何尺寸,建立有限元計算模型。模型選用具有三角形退化功能的PLANE55,采用自由網格劃分,單元長度為0.1 m。溫度荷載以約束的形式施加在橋塔塔壁內外表面。有限元模型見圖11。此外,導熱系數取2.4 J/(m·s·K),比熱容取值為950 J/(kg·K)。

圖11 混凝土橋塔溫度場分析模型

3.3 橋塔橫斷面溫度分布

以塔壁厚度方向、塔壁長度和寬度方向實測最不利的正溫差、負溫差值見表1。并計算了沿塔壁厚度方向、塔壁長度和寬度方向的溫差梯度分布。

表1 各塔壁最不利溫差值 ℃

以橋塔截面厚度方向的最大正向溫差和最大反向溫差計算得截面厚度方向的溫度分布,建議厚度方向的溫度分布采用線性分布,如圖12所示。

圖12 塔壁厚度方向的溫度分布

根據混凝土橋塔溫度場的測試值,參考我國《鐵路橋涵設計規范》(TB10002.3—2005)[11]給出的板厚方向的溫差基數,建議橋塔厚度方向正溫差基數取為10 ℃,負溫差基數為-10 ℃。

建議長寬方向分別出現最大溫差時的正溫差梯度和負溫差梯度曲線見圖13，圖14。

圖13 長度方向溫度梯度曲線

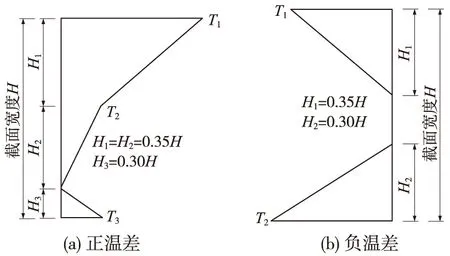
圖14 寬度方向溫度梯度曲線

從3個季節橋塔溫度場的測試資料來看,橋塔長度和寬度方向的正溫差均未超過10 ℃,負溫差均未超過-6 ℃。偏于保守考慮,建議正溫差梯度基數參考我國《公橋橋涵設計規范》(JTG D60—2004)[12]、《鐵路橋涵設計規范》(TB10002.3—2005)[11]和英國規范(BS5400)[13]進行取值,但應參照不考慮橋面鋪裝或是無砟橋面下混凝土箱梁的溫度梯度基數。負溫差梯度基數參考我國《公路橋涵設計規范》(JTG D60—2004)[12],取正溫差的-0.6～-0.7倍。

4 結語

(1)3個季節下,塔外環境溫度及塔壁外表面溫度隨時間變化近似均呈正弦曲線變化趨勢,日較溫差較大；塔內環境溫度及塔壁內表面的溫度隨時間變化不明顯,日較溫差較小。

(2)3個季節下,塔壁厚度方向的最大正溫差相差不大,都在8 ℃左右；最大負溫差有所不同,冬季和春季的最大負溫差均比夏季的負溫差大,冬季和春季的最大負溫差在-6 ℃～-7 ℃,而夏季的最大負溫差未超過-2 ℃。

(3)3個季節下,塔壁長度和寬度方向的溫差也不容忽視,在春季橋塔溫度場測試結果顯示,最大溫差可達到9 ℃以上,其余兩個季節的溫差也在6 ℃左右。

(4)計算分析表明,塔壁厚度方向、長度和寬度方向溫度梯度模式宜采用折線分布。

參考文獻：

[1] Churchward A,Sokal Y J. Prediction of Temperature in Concrete Bridges[J]. Journal of Structural Division,ASCE,1981,107(11):2163-2176.

[2] Fu H.C,Ng S.F,Cheung M.S. Thermal behavior of composite bridges[J]. Journal of Structura1 Engineering,ASCE,1990,116(12):3302-3323.

[3] Chang S.P.,Im C.K. Thermal behavior of composite box-girder bridges[J]. proc. of the Instn Civ. Engrs Structs & Blds,2000,140:117-126.

[4] 葉見曙,賈琳,錢培舒.混凝土箱梁溫度分布觀測與研究[J].東南大學學報,2002,32(5):788-793.

[5] 賈琳.陽輻射作用下混凝土箱梁的溫度分布及溫度應力研究[D].南京：東南大學,2001.

[6] 顏東煌,涂光亞,陳常松,等.肋板式主梁溫度場的數值計算方法[J].中外公路,2002,22(2):45-48.

[7] 彭友松.混凝土橋梁結構日照溫度效應理論及應用研究[D].成都：西南交通大學,2007:1-16.

[8] 王勇軍.時速200 km客貨共線鐵路空心橋墩溫度應力分析[J].鐵道標準設計,2010(6):59-62.

[9] 葛耀君,翟東,張國泉.混凝土斜拉橋溫度場的試驗研究[J].中國公路學報,1996,9(2):76-82.

[10] 王勖成.有限單元法基本原理和數值方法[M].北京：清華大學出版社,2002:421-438.

[11] TB10002.3—2005 鐵路橋涵設計基本規范[S].北京：中國鐵道出版社,2005.

[12] JTG D60—2004.公路橋涵設計通用規范[S].北京：人民交通出版社,2004.

[13] BS5400.英國標準5400-鋼橋、混凝土橋及結合橋[S].西安：西南交通大學出版社,1978.