一種改進的線性圖像插值算法
高放,趙杰
(河北大學 電子信息工程學院,河北 保定 071000)
隨著計算機圖形學與數字圖像處理技術的發展,圖像插值技術也應運而生。所謂圖像插值就是一個圖像數據再生的過程。從硬件上著手圖像插值,可以獲得較高的圖像質量,但需要付出較昂貴的代價,基于此,從軟件方面進行改進,則顯得更有意義。
傳統的圖像插值方法有最近鄰插值,雙線性插值,雙立方插值等[1]。最近鄰插值算法簡單,運算速度快,但插值質量差,容易出現鋸齒、方塊效應;雙線性插值雖然減輕了鋸齒和方塊效應,但它的平滑作用會使圖像細節產生退化,圖像變得模糊;雙立方插值較好的改進了這一點,但運算量巨大,不適合實時應用[2]。近年來許多學者又提出了一些基于邊緣和梯度[3-4]的圖像插值算法,取得了好的視覺效果,但是計算量都很大。筆者提出了一種改進的線性插值算法,根據待插值點所處的位置選擇合適的已知點進行插值,計算簡單,經實驗證明,該算法能有效的保持圖像邊緣,提高了圖像的質量。
1 本文算法
本文對一幅圖像的插值分為兩步,先進行矩形插值,再進行梅花插值,即先插值行列和為偶數的點,再插值行列和為奇數的點[5]。在每步插值過程中將待插值點進行分類,對不同類的待插值點分別選取最佳的已知點進行插值。
1.1 矩形插值
一般情況下,一幅圖像可以劃分為幾個不同的區域,不同的區域有著不同的特征,就灰度圖像來說,同一區域內各像素的灰度值相近,不同的區域間像素灰度值差異較大。在一個區域與另一個區域之間存在著邊緣。所謂圖像邊緣就是一個區域與另一個區域的分界線,表明一個區域的終結和另一個區域的開始。如果一幅圖像中存在邊緣,則邊緣是“成對”的,如圖 1(a),A1,A2為區域 A 內的兩個像素點,B1,B2為區域B內的4個像素點,由對邊緣的定義可知,A1,A2表示區域A的終結,為區域A的邊緣,B1,B2表示區域B的開始,為區域B的邊緣,即A1,A2與B1,B2都為邊緣,所以說邊緣是“成對”的。另外,圖1(a)中的 B2,B3與C1,C3為一對斜邊緣。
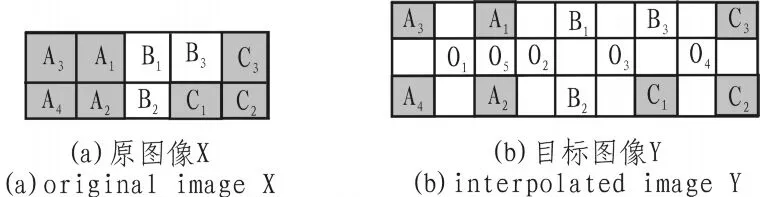
圖1 原圖像與目標圖像Fig.1 Edges in the image
首先假設原圖像為X,如圖1(a),插值后的目標圖像為Y,如圖1(b)。本文將待插值點分為3類,下面分別介紹了這3類待插值點的特征,并且分析了采用傳統的雙線性插值法對其插值結果的影響。
第1類待插值點處于一個區域的內部,以O1為例。由圖可知O1處于區域A的內部,其對應原圖像中的4個相鄰點分別為 A1,A2,A3,A4,令其灰度值為 f(Ai),i=1,2,3,4,由于它們同屬于區域A,所以其灰度值相近,因此,O1四鄰域內任何方向(垂直、水平、兩個對角方向)上的像素灰度差值都較小。對其進行雙線性插值如下:
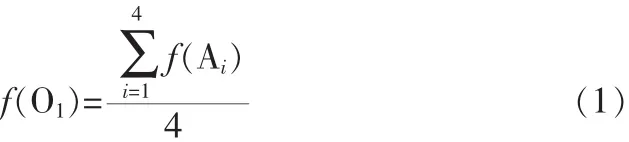
由(1)式可知,對O1的插值結果也表現為區域 A的特征。因此,此類待插值點適合采用傳統的雙線性插值法。
第2類待插值點位于某一區域的邊緣上。此類分兩種情況即位于45°對角線邊緣上或135°對角線邊緣上,在此以位于區域C的45°對角線邊緣上的O4為例,其4個相鄰點分別為 B3,C1,C2,C3,由于 B3與 C1,C2,C3屬于不同的區域,故沿45°度對角線方向上的像素灰度值差值較小,而沿135°方向上的像素灰度值差值較大(當待插值點位于135°對角線邊緣時特征正好相反),對其進行雙線性插值:
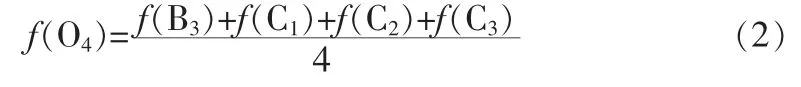
由式(2)可知,O4的灰度值由區域B和區域C的像素點灰度值共同決定,使得O4混合了區域B和區域C的特征,而O4本屬于區域C,因此平滑掉了區域B,C間的差異,造成了邊緣模糊。由此可見,采用傳統的雙線性插值對此類待插值點的插值效果并不理想。
第3類待插值點位于兩個區域之間。此類也分兩種情況即位于兩個水平區域之間或兩個垂直區域之間,在此以位于2個垂直區域A,B之間的O2為例,其4個相鄰點分別為A1,A2,B1,B2。沿垂直方向上的像素灰度差值都很小(當位于兩個水平區域之間時沿水平方向上的像素灰度差值都很小),其他任何方向上的灰度差值都較大。對其進行雙線性插值:
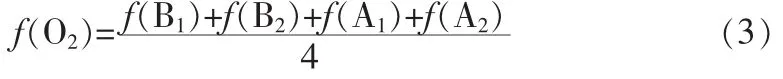
同樣,O2混合了區域A和區域B的特征,平滑掉了區域A,B間的差異,造成了邊緣模糊。對此類待插值點進行雙線性插值的效果也不理想。
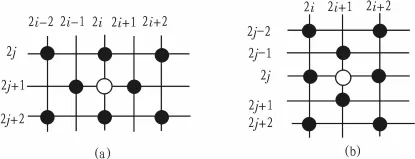
由上面的分析可知,采用傳統的雙線性插值法對第2類與第3類待插值點進行插值時之所以會產生邊緣模糊,原因在于插值時選取了不同區域的已知點,如果只選取同一區域的已知點,即待插值點的灰度值只由一個區域的像素點灰度值決定就會避免這種現象。本文基于此進行了改進,先計算待插值點四鄰域內各個方向上的灰度差值,通過與閾值T比較來判斷該點屬于哪一類,若為第一類則直接雙線性插值;若為第二類則先判斷邊緣方向,只沿該邊緣方向插值;若為第三類則先判斷區域方向,取灰度差值最小的那個區域中的兩個已知點進行插值。具體算法如下:設待插值點為Y2i+1,2j+1,取其在原圖像中對應的2×2鄰域,如圖2,分別計算其水平、垂直、兩個對角線方向上的像素灰度值之差,如式(4)。

圖2 待插值點的2×2鄰域Fig.2 2×2 Neighborhood of Interpolated Pixel

設Dmax=MAX(Di)Dmin=MIN(Di)i=h1,h2,v1,v2方法步驟如下,其中T為預先設置的閾值。If Dmax %以下待插值點都為第3類 矩形插值后,利用原圖像已知像素點與矩形插值中計算出的像素點對行列和為奇數的點進行插值。行列和為奇數的點有兩種:位于偶數行奇數列上的點(如圖3(a)中的點(2i,2j+1))和位于奇數行偶數列上的點(如圖 3(b)中的點(2i+1,2j))。本文以點(2i,2j+1)為例來說明。步驟同矩形插值,先求出待插值點四鄰域各方向上的像素灰度差值,通過閾值判斷進行分類,然后選取合適的點插值。具體步驟如下: 圖3 行列和為奇數的點Fig.3 Pixels whose sum of line and column is odd number 采用本文的算法與雙線性法和雙立方法分別對灰度圖像lena和pepper用matlab[6]進行同樣倍率的插值,比較插值后原圖像與插值后圖像的峰值信噪比(PSNR)。PSNR[7]反映了插值圖像與原圖像相符合的程度,其值越大越好,它的定義如(6)式。 其中,f(i,j),g(i,j)分別對應原圖像和插值圖像在點(i,j)上的取值;M、N 分別是原始圖像中行(i)、列(j) 像素點的個數;L是圖像中灰度值的取值范圍,對8比特的灰度圖像而言L=255。比較結果如表1所示。 表1 不同插值算法的PSNR比較Tab.1 Test result of photoelectric conversion circuit 圖4顯示了對lena灰度圖像分別用雙線性、雙立方和本文算法進行2倍插值后的圖像視覺效果。從圖中可以看出,用雙線性插值法得到的插值圖像存在邊緣模糊的現象,雙立方法有顯著的改進。本文算法視覺優于雙線性算法,與雙立方算法效果相當,但計算量遠遠小于雙立方法。 圖4 對Lena采取3種插值方法的效果圖Fig.4 Visual effects of lena 本文提出了一種改進的線性插值算法,先根據待插值點所處的位置對其進行分類,然后根據類別選取最佳的已知點進行插值。實驗結果表明,該算法運算速度快,插值效果與雙立方插值效果相當,改進了傳統雙線性插值邊緣模糊的現象,插值生成的圖像更加清晰,有較好的視覺效果。 [1]符祥,郭寶龍.圖像插值技術綜述[J].計算機工程與設計,2009,30(1):141-144.FU Xiang,GUO Bao-long.Overview of image interpolation technology[J].Computer Engineering and Design,2009,30(1):141-144. [2]陳建輝,王博亮,徐中佑,等.一種自適應最大相關性數字圖像插值算法[J].廈門大學學報:自然科學版,2005,44(3):355-358.CHEN Jian-hui,WANG Bo-liang,XU Zhong-you,et al.An adaptive max-relativity interpolation algorithm for digital image[J].Journal of Xiamen University:Natural Science,2005,44(3):355-358. [3]張美玉,王孝通,徐曉剛.改進的圖像自適應梯度插值[J].中國圖像圖形學報,2009,14(5):853-858.ZHANG Mei-yu,WANG Xiao-tong,XU Xiao-gang.An improved adaptive image interpolation with gradient features[J].Journal of Image and Graphics,2009,14(5):853-858. [4]謝美華,王正明.基于圖像梯度信息的插值方法[J].中國圖像圖形學報,2005,7(10):856-861.XIE Mei-hua,WANG Zheng-ming.Image interpolation based on gradient[J].Journal of Image and Graphics,2005,7(10):856-861. [5]黨向盈,吳錫生,趙勇.基于邊緣最大相關性的快速圖像插值算法[J].計算機應用,2006,26(12):2880-2883.DANG Xiang-ying,WU Xi-sheng,ZHAO Yong.Fast image interpolation algorithm based on edge-directed max-relativity[J].Computer Applications,20076,26(12):2880-2883. [6]胡曉軍,徐飛.Matlab應用圖像處理[M].西安:西安電子科技大學出版社,2011. [7]王會鵬,周利莉,張杰.一種基于區域的雙三次圖像插值算法[J].計算機工程,2010,36(19):216-218.WANG Hui-peng,ZHOU Li-li,ZHANG Jie.Region-based bicubic image interpolation algorithm[J].Computer Engineering,2010,36(19):216-218.
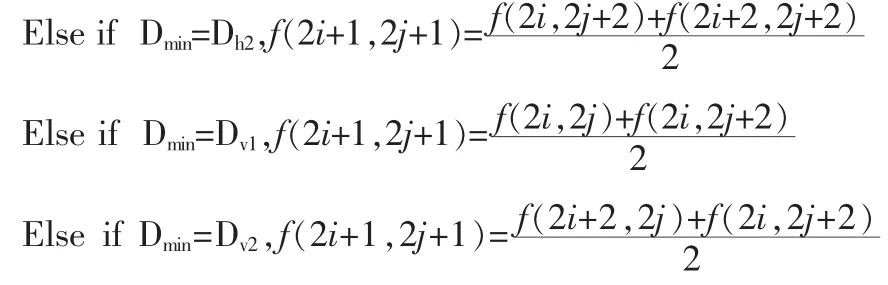
1.2 梅花插值

2 實驗分析
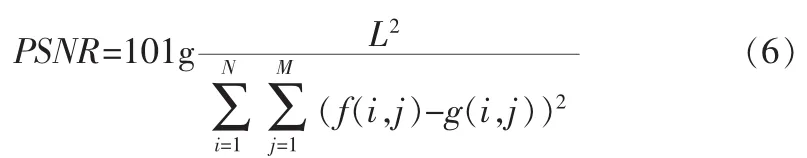


3 結 論

