基于Chebyshev多項式逼近的分數階微積分數值算法

陳 安， 李常品

(上海大學理學院，上海200444)

分數階微積分擁有長達300多年的歷史，但直到近幾十年才得到快速發展［1］.這主要是因為分數階能夠比整數階更好地刻畫現實中的復雜模型，尤其是對一些具有記憶與遺傳性質的物質的刻畫［2］.不過也正因為分數階微分的非局部性，導致了其數值計算的困難.Diethelm等［3］總結了關于分數階微積分的幾種常見的數值算法，本質上是利用函數的線性插值來構造相應的數值公式.Yuan等［4］構造了一種新的數值格式，這種格式能有效地避免因分數階微分的非局部性而引起的高計算復雜度.之后，Diethelm［5］對該格式進行了改進，改進方法的主要思想是把原問題轉化為更易求解的積分問題，然后利用 Gauss公式求解.為了得到更高階的算法，Miyakoda等［6-8］基于Chebyshev多項式建立了一種新數值格式，然而，他們僅討論了分數階微分(t)在0＜α＜1時的情況.Li等［9］基于插值函?數，對分數階微積分提出了幾種新的有效數值算法.關于分數階偏微分方程的有限元方法可參見文獻［10-12］，其中文獻［11］是關于分數階偏微分方程間斷有限元方法的早期工作，文獻［12］是關于分數階超擴散問題有限元方法的早期工作.

本工作基于Chebyshev多項式逼近建立了高階的分數階積分與Caputo型分數階導數的數值算法，推廣了文獻［6-8］中α的應用范圍.

下面，首先給出2個相關的基本定義.

定義1 關于函數 f(t)分數階積分的定義如下：

定義2 關于函數f(t)的Caputo型分數階導數的定義如下：

1 分數階微積分數值算法的建立

為了簡便起見，對式(1)和(2)僅考慮a=0及0≤t≤1時的情況，其中對式(2)只討論m=2時的情況(m=1時的情況可參見文獻［7-8］).

1.1 分數階積分數值算法

利用移位Chebyshev多項式Tk(2t－1)對式(1)中的f(t)進行逼近［7-8］，有

式中，

其中插值節點為

Chebyshev多項式 Tk(x)可用如下遞歸公式得到：

將式(3)代入式(1)，有

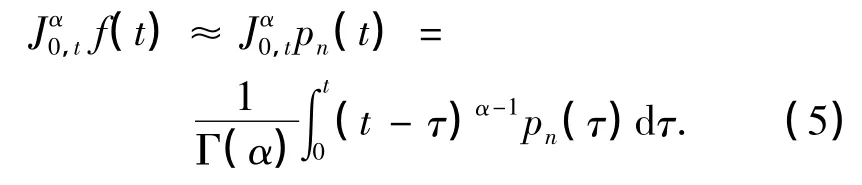
為了得到式(5)的具體表示，給出下面的引理.

引理1 記pn為式(3)的n次多項式，則存在相應的階數為n的多項式Ln，滿足

證明 對pn(τ)在t處Taylor展開，有

首先，在引理1中取x=0并對其化簡，得到

然后，式(6)兩邊同時對x求導，整理，有

由式(7)可知

從而

將式(3)，(9)及(11)代入式(8)，得

注意到，只需知道式(9)中bi的值便可以推導出分數階積分的數值表達式，因此，對比式(12)中左右兩邊Ti(2x－1)(i=1，2，…，n)前的系數，并整理，得到

綜上，可得到關于分數階積分(1)的數值算法如下：

式中，α＞0，t∈［0，1］，而ak及bk可分別由式(4)和(13)得到.

1.2 Caputo型分數階導數的數值算法

下面主要討論式(2)中1＜α＜2時的情況，對于0＜α＜1時的情況可參見文獻［7］.

類似于分數階積分數值算法的討論，仍利用移位Chebyshev多項式對f(t)進行逼近

式中，pn可由式(3)得到.下面給出一個引理，其證明過程類似引理1，這里不再贅述.

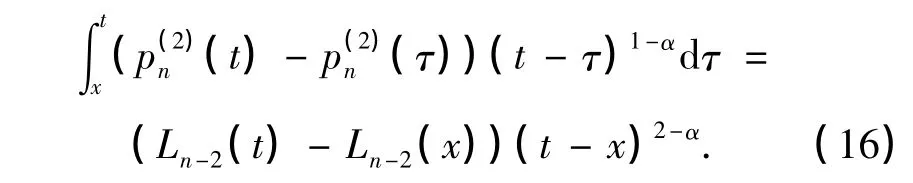
令x=0，并化簡，得

因此，由式(15)可以進一步得到

為了得到式(17)右端的具體表示，首先在式(16)兩邊同時對x求導，整理后，得

然后，結合式(10)，有

為了確定式(19)中的bi，把式(19)和(20)代入式(18)，并整理，得

由于只需知道式(19)中的bi，i=1，2，…，n－2，則對比上式兩邊Tk(2x－1)前的系數，整理，于是得到

綜上，得到Caputo型的分數階導數的數值算法如下：

式中，α∈(1，2)，t∈［0，1］，而dk，bk分別由式(21)和(22)決定.

我們在建立數值算法(式(23))時發現，對于α可進一步推廣至α＞2時的情況，這里不再重述其推導過程.

2 誤差分析

下面依次給出式(5)和(15)的誤差分析.由文獻［7，13］可以得到

下面給出式(5)的一致有界性，即其與t在區間［0，1］的取值無關.

引理3 基于Chebyshev多項式pn(t)逼近的分數階積分的數值算法是一致有界的，即

式中，

證明 注意到，|Tn+1(2t－1)－Tn－1(2t－1)|≤2，故|f(t)－pn(t)|≤2Mn，從而結合式(5)，有

定理1 假設 f(z)在 Cr上解析，則基于Chebyshev多項式pn(t)逼近的分數階積分的數值算法有如下誤差估計：

結合引理3，有

最后，給出式(15)的誤差估計.為了討論的方便，記

這樣，式(24)可寫成

下面給出一個引理.

引理4 基于Chebyshev多項式pn(t)逼近的Caputo型分數階導數的數值算法是一致有界的，即

式中，

證明 由于E″n(t)=A″n+1(t)Bn(t)+2A'n+1(t)· B'n(t)+An+1B″n(t)，另外，根據Chebyshev多項式的相關性質，可以得到如下估計：

因此，

定理2 假設f(z)在Cr上解析，則基于Chebyshev多項式pn(t)逼近的Caputo型分數階導數的數值算法有如下誤差估計：

證明 由定理1的證明過程易得

且

從而有

對上式進行估計，有

因此，把式(27)～(29)代入引理4中的式(26)，整理，即可證明.

定理1及定理2中的“O”表示當n趨向無窮大時，數值算法誤差的收斂速度的快慢.容易看出，本工作提出的基于Chebyshev多項式逼近建立的分數階積分數值算法(式(14))及Caputo型分數階導數數值算法(式(23))具有較快的收斂速度.

3 數值算例

設f(t)=tβ，則

在式(14)中取β=4，在式(23)中取β=5，則可分別得到對應的n的分數階積分及Caputo型分數階導數的數值解，同時，將它們與文獻［3］中的線性插值方法相比較.

從表1和表2中的誤差結果可以發現，對本算例而言，在分數階積分的數值格式中，n=4時的收斂速度要比n=2時好得多;而在分數階微分的數值格式中，n=8時的收斂速度要比n=4時好得多.對于其他情況，則可根據相應的f(t)來變動n值.此外，通過對比2種不同的計算方法的數值結果可知，本工作建立的分數階積分及Caputo型分數階導數的數值算法，即式(14)與(23)，它們的收斂速度均高于文獻［3］中所提及的線性插值方法，且推廣了文獻［7］中的數值方法.

表1 的絕對誤差Table 1 Absolute error of

表1 的絕對誤差Table 1 Absolute error of

α絕對誤差線性插值法［3］Chebyshev多項式逼近法(式(14 =4 0.2 6.810 969E－002 2.226 088E－002 2.652 089E－n=2 n=4 )) n=2 n 002 3.330 669E－016 0.6 1.013 351E－001 2.868 810E－002 2.709 820E－002 2.220 446E－016 1.4 5.349 327E－002 1.272 141E－002 5.929 401E－003 1.249 001E－016 1.8 3.183 041E－002 7.270 493E－003 1.188 870E－002 2.081 668E－017

表2 的絕對誤差Table 2 Absolute error of

表2 的絕對誤差Table 2 Absolute error of

α絕對誤差線性插值法［3］Chebyshev多項式逼近法(式(23 =8 1.2 3.600 270E－001 9.147 084E－002 7.433 626E－n=4 n=8 )) n=4 n 002 8.881 784E－016 1.4 3.912 311E－001 1.020 049E－001 2.053 614E－001 1.065 814E－014 1.6 3.802 527E－001 1.030 250E－001 4.273 832E－001 1.065 814E－014 1.8 2.787 430E－001 7.964 166E－002 7.920 905E－001 2.486 900E－014

［1］ PODLUBNYI.Fractional differential equations［M］.San Diego，CA：Academic Press，1999：261-307.

［2］ 徐明瑜，譚文長.中間過程、臨界現象——分數階算子理論、方法、進展及其在現代力學中的應用［J］.中國科學：G輯，2006，36(3)：225-238.

［3］ DIETHELMK，FORDN J，FREEDA D，etal.Algorithms for the fractional calculus：a selection of numerical methods［J］.Comput Methods Appl Mech Eng，2005，194：743-773.

［4］ YUANL，AGRAWALO P.A numerical scheme for dynamic systems containing fractional derivatives［J］.ASME J Vibr Acoust，2002，124：321-324.

［5］ DIETHELM K.An improvementofanonclassical numerical method forthe computation offractional derivatives［J］.Numer Algor，2009，131(1)：014502-4.

［6］ MIYAKODAT.Discretized fractional calculus with a series of Chebyshev polynomial［J］.Electronic Notes Theor Comput Sci，2009，225：239-244.

［7］ SUGIURAH，HASEGAWAT.Quadrature rule for Abel’s equations：uniformly approximating fractional derivatives［J］.J Comput Appl Math，2009，223：459-468.

［8］ HASEGAWAT，SUGIURAH.Uniform approximation to fractional derivatives of functions of algebraic singularity［J］.J Comput Appl Math，2009，228：247-253.

［9］ LIC P，CHENA，YEJ J.Numerical approaches to fractional calculus and fractional ordinary differential equation［J］.J Comput Phys，2011，230(9)：3352-3368.

［10］ ZHENGY Y，LIC P，ZHAOZ G.A note on the finite elementmethod for the space-fractional advection diffusion equation［J］.Comput Math Appl，2010，59 (5)：1718-1726.

［11］ ZHENGY Y，LIC P，ZHAOZ G.A fully discrete discontinuous Galerkin method for nonlinear fractional Fokker-Planck equation［J］.Mathematical Problems in Engineering，2010，doi：10.1155/2010/279038.

［12］ LIC P，ZHAOZ G.Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion［J］.Comput Math Appl，2011，62(3)：855-875.

［13］ ELLIOTTD.Truncation errors in two Chebyshev series approximations［J］.Math Comput，1965，19：234-248.