例析初中數學解答中的幾種典型錯誤

☉江蘇省南通市通州區興仁中學 張玉娟

例析初中數學解答中的幾種典型錯誤

☉江蘇省南通市通州區興仁中學 張玉娟

學習是從未知走向已知的過程，學習的階段性成果如何可以通過具體的問題的解答來反映，在問題解答中學生出現錯誤是在所難免的，其中有些錯誤還具有典型性，我們在平時的教學和復習中，應予以重點關注，適度地進行強化，確保學生解題能力的提升，除了在中考數學考試中發揮出較高的水平以外，也促進今后的數學學習思維更為縝密.筆者就學生在答題中經常出現的錯誤類型進行分析，與大家商榷.

一、對根的判別式的忽視導致錯誤

二、對幾何圖形不唯一性的忽視導致錯誤

例2 已知△ABC為等腰三角形，AB＝AC，且AB的垂直平分線與AC所在的直線相交成50°的銳角，試求∠B的大小.

三、對二次根式化簡時公式成立條件的忽視導致錯誤

四、缺乏分類討論的意識導致錯誤

例4 如圖3所示，已知射線DE分別與x軸、y軸交于D、E兩點，坐標分別為（3，0）和（0，4），現在有一動點C由點M（5，0）出發，沿x軸向左以1個單位長度/秒的速度做勻速運動，與此同時，另一動點P由點D點出發，沿射線DE的方向以相同的速度做勻速運動.設運動時間為t秒，求以下幾個問題：

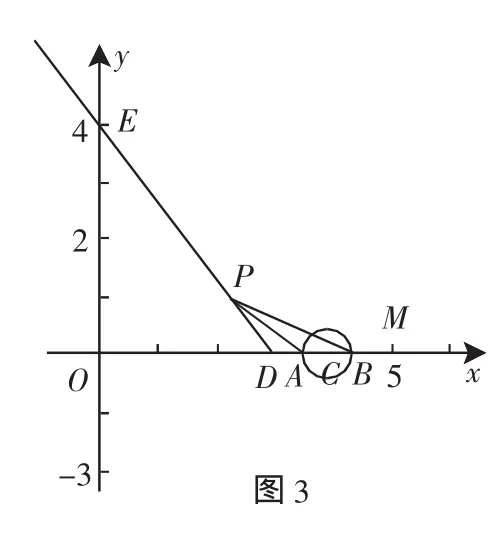
錯因分析：對于第三個小問題，學生不容易做全，因為如果△PAB為等腰三角形，則應該存在三種可能情況：PA＝AB，或者PA＝PB，或者PB＝AB，需要進行討論.而學生由于思維定勢，沒有多加考慮，大多只能完成其中的一種PA＝PB最為簡單的情況，而導致出現了遺漏，與正確的解答失之交臂.

正確解答：（3）如果△PAB為等腰三角形，則應該存在三種可能情況：PA＝AB，或者PA＝PB，或者PB＝AB.

五、結語——教學應強化學生觀察問題的能力

如何有效防止典型錯誤的發生？觀察問題是解決問題的前提，注意對問題進行觀察，發現問題所涉及到的數學概念和模型.當然問題的觀察點有可能存在多個，這樣一來就探索出一題的多種解法，學生的解題能力也在觀察和遷移中有所提升.首先，引導學生搞清題設的條件和結論，區分題目中所給的數學概念和文字的含義，如果是比較抽象的描述，應對條件和結論進行必要的分解.其次，對于條件和結論，應盡量轉化為數學符號或是圖形等直觀化的表征形態，幫助理解概念和問題情境.最后，注意題目非表面的數學信息的挖掘，這些非表面的信息，必須在觀察后經過一番思索才能看到其隱藏著的一些條件和特征.