基于數學形態濾波的大地電磁強干擾分離方法

湯井田，李晉，肖曉，徐志敏，李灝，張弛

（中南大學 地球科學與信息物理學院，湖南 長沙，410083）

基于數學形態濾波的大地電磁強干擾分離方法

湯井田，李晉，肖曉，徐志敏，李灝，張弛

（中南大學 地球科學與信息物理學院，湖南 長沙，410083）

針對礦集區大地電磁信號采集過程中常引入強噪聲干擾等問題，采用數學形態濾波對大地電磁強干擾分離方法進行研究。在仿真信號中加入常見的強干擾來檢驗形態濾波的降噪能力，根據噪聲類型選取不同結構元素尺寸及大小，并將形態濾波應用于實測大地電磁數據的降噪處理。采用非線性共軛梯度法進行反演，考查形態濾波對提高大地電磁測量數據質量的改善情況。研究結果表明：數學形態濾波能有效消除大地電磁強干擾中的大尺度干擾和基線漂移現象，重構信號基本保留原始大地電磁信號特征，改善大地電磁測深數據質量。由于該方法原理簡單、并行運算速度快，具有較好的應用價值，適合于礦集區海量大地電磁強干擾分離。

形態濾波；大地電磁；強干擾分離；結構元素

礦產資源是國民經濟和社會發展的重要物質基礎，隨著地表資源勘查程度的提高，礦床發現的難度越來越大，必須增加勘探深度，向深部索取資源，以不斷滿足我國經濟高速發展對資源的需求。大地電磁測深法（Magnetotelluric，MT）自20世紀50年代初提出以來，隨著科學技術的不斷進步，尤其是計算機技術及現代數字信號處理技術的發展，使得MT得到了飛速發展，已成為礦區找礦、海洋地質調查、工程勘

探、地震預報、油氣田普查勘探、巖石圈結構探測、地下水和尋找地熱資源等領域的重要手段。大地電磁測深理論提出至今，噪聲問題一直困擾著廣大MT研究者，如何抑制噪聲，提高MT測量數據質量，是國內外共同關注的課題[1?3]。目前大地電磁去噪方法存在一定的局限性，如遠參考處理法從理論與實踐結果看，能成功消除局部相關噪聲，但是，經遠參考處理后，單點數據的誤差棒變大，特別是在處理受電磁干擾嚴重和校正量較大的數據段時，該現象尤為明顯[4]；Robust處理法無法消除輸入端的噪聲，且Robust法無法剔除噪聲較多和能量較強時的近源電磁相關噪聲對數據的干擾[5]；小波變換則過分依賴于小波函數的選取，有時隨著尺度增大，相應正交基函數的頻譜局部性變差，使其對大地電磁信號更精細分解受到限制[6]；HHT法雖然不要選擇基函數，與小波變換相比具有更強的時頻刻畫能力，但因EMD分解是自適應的，無法揭示每時段的頻率特性和能量差異所具有的細微變化，且算法占用大量運算時間，不適合對實測大地電磁信號進行處理[7]；人機聯作法雖能較好地改善數據質量，但操作時參與了太多的人為因素，而且耗費很多時間和精力，且操作者必須具備豐富的噪聲識別經驗，否則效果適得其反[8]。由于礦集區人口稠密、現代通訊設備先進、交通發達及礦產資源豐富、民間開采廣泛等因素導致MT數據采集與處理相當困難。大地電磁場具有很寬的頻率范圍，鑒于其激發機制不同，大地電磁信號表現出的形態和頻譜特征也各有差異，且極易受各種噪聲干擾，是典型的非線性和非平穩信號。由于野外觀測數據不可避免地受到各種噪聲的污染，且電磁噪聲干擾日益嚴重，導致大地電磁采集數據的一致性和重復性變差，曲線參數的魯棒性也變差，使估算分散不能客觀地反映地下電性分布情況，甚至得到錯誤的結論。如何應用現代數字信號處理技術剖析大地電磁強干擾信號特征，得到無偏的阻抗估計是取得良好勘探結果的關鍵。尤其是在礦集區，礦山的開采、冶煉及與其配套的重工業密集形成的電磁噪聲和人文噪聲非常復雜，導致測量得到的視電阻率失真嚴重。因此，研究MT噪聲的特點和MT測量數據中的信噪識別和處理技術，對改善MT測量數據質量、探測地殼精細結構及尋找深部控礦構造具有非常重要的實際應用價值。在此，本文作者針對大地電磁噪聲的上述特點，引入數學形態濾波進行探討，針對不同的噪聲類型選擇不同的結構元素尺寸及大小，構造適合大地電磁強干擾分離的形態濾波器，并對礦集區實測大地電磁強干擾進行降噪處理。

1 數學形態濾波

數學形態學（Mathematical morphology，MM）是基于積分幾何和隨機集合論等數學理論建立起來的1種非線性信號處理方法。該算法是用集合來描述目標，集合各部分之間的關聯表明目標信號的結構特點，即考察目標信號時設計1個稱為結構元素的“探針”，通過探針在信號中不停地移動來考察信號各部分之間的關聯，從而提取出有用的信息進行結構分析和描述。該方法利用結構元素對信號的幾何特征進行局部匹配或修正，同時保留目標信號主要的形狀特征，以達到提取有用信息、保持細節成分和抑制噪聲的目的。形態濾波器是從數學形態學發展起來的一種新型非線性濾波技術，近年來，隨著形態學理論的飛速發展，形態學濾波被逐步推廣到一維信號處理領域[9?11]。

1.1 基本形態變換

數學形態學的基本變換為膨脹和腐蝕，膨脹和腐蝕變換等價于離散函數在滑動濾波窗（相當于結構元素）內的最大值和最小值濾波。其中，膨脹變換表示1種擴張變換，使目標肢體擴張，孔洞收縮，用來填平邊界不平滑的凹陷部分，增大了谷值，擴展了峰頂。腐蝕變換表示1種收縮變換，使目標肢體收縮，孔洞擴張，用來剔除邊界不平滑的凸起部分，減少了峰值，加寬了谷域。其定義如下。

設輸入信號f（n）為定義在Df={x0，x1，…，xn}上的離散函數，結構元素g（m）為定義在Dg={y0，y1，…，ym}上的離散函數，且n＞＞m。則f（n）關于g（m）的膨脹和腐蝕運算分別定義為：

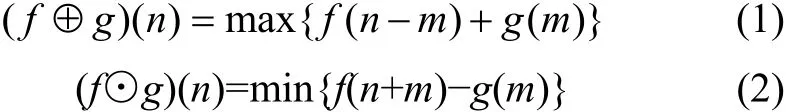
式中：⊕和⊙分別表示膨脹和腐蝕運算。

形態開和形態閉運算是膨脹和腐蝕運算的衍生運算，f（n）關于g（m）的形態開和形態閉運算分別定義為：

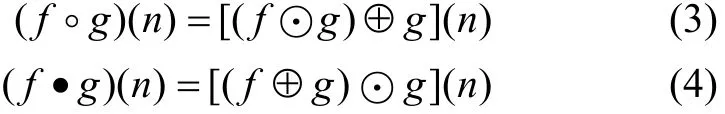
式中：“?”和“·”分別表示形態開和形態閉運算。其中：形態開運算是對結構元素先腐蝕后膨脹，用來消除目標信號中的細節、孤立點及疊加在信號上窄的“毛刺”，目的是使目標信號的輪廓光滑，從而剔除尖峰，抑制正脈沖（峰值）噪聲；形態閉運算是對結構元素先膨脹后腐蝕，用來彌補目標信號中的孔洞及很窄的“裂縫”，目的是填平谷底，抑制負脈沖（低谷）噪聲。開、閉運算均具有低通特性，在實際應用中，常采用形態開、閉運算或形態開、閉運算的級聯形式相結合來濾除目標信號中的正、負脈沖噪聲。

十六大以來，2002年到2012是我國GDP增長最快的十年，國內GDP增速超過兩位數，也一躍成為世界第二大經濟體。然而從2012年開始，中國經濟已然告別了高速增長期，開始了被稱之為＂新常態＂的新階段，GDP增長率也從2011年接近百分之十下降到2016年的6.7%，這已經是自上世紀九十年代以來所出現的最低增速。

1.2 構建形態濾波器

Maragos和Schafer采用同一類型和尺寸的結構元素，通過不同順序級聯形態開、閉運算，定義了形態開?閉FOC（f（n））和閉?開濾波器FOC（f（n））[12?13]：

由式（5）和（6）可知：形態開?閉和形態閉?開濾波器都能同時去除目標信號中的正、負脈沖干擾，具有形態學中開、閉運算的所有性質。但是，由于形態開運算的收縮性導致形態開?閉濾波器輸出偏小，而形態閉運算的擴展性導致形態閉?開濾波器輸出偏大。因此，目標信號在濾波過程中存在統計偏倚現象[14]，直接影響到濾波器的噪聲抑制性能。為了有效去除各種噪聲干擾和抑制統計偏倚現象，采用級聯開、閉運算構造形態開?閉和形態閉?開組合形態濾波器作為輸出，用于大地電磁強干擾噪聲的分離：

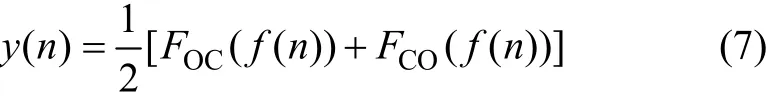
式中：y（n）表示組合形態濾波器的輸出結果。重構的大地電磁信號ε（n）定義為：

1.3 選取結構元素

形態濾波的質量取決于所選擇的形態變換和結構元素。結構元素在形態運算中的作用類似于一般信號處理中的濾波窗口或參考模板，其尺寸和形狀都將對形態學基本變換產生很大影響。采用不同的結構元素可以提取出目標信號中不同的形狀特征，選取的結構元素要盡可能接近待分析信號的形狀特點。常見的結構元素有直線型、三角型、圓盤型、正弦型、拋物線型以及其他多邊形組合。待處理信號的形狀通常決定了結構元素的形狀設計，一般一種結構元素對一類噪聲有較好的濾除效果。相對而言，結構元素越復雜，其濾除噪聲的能力就越強，但所耗費的時間也就越長[15]。

2 礦集區典型強干擾類型分析

圖1所示為安徽省廬樅礦集區某測點的一段實測大地電磁原始數據，測量數據由加拿大鳳凰公司生產的V5-2000儀器采集。對該段數據出現強干擾的時間序列進行分析可知：電道和磁道均不同程度地受到了周期性的突跳和波動等信號干擾，這些信號與穩定的天然電磁場信號相比，具有振幅大、能量強和周期性明顯等特征。因此，將時域信號中出現的明顯非天然電磁場的信號定為噪聲信號。對大量MT測量數據的時間序列特征進行分析可知：電道數據常被強度大的方波噪聲干擾，造成電道曲線整體基線漂移嚴重，對低頻數據的影響巨大；磁道數據常被大尺度充放電三角波噪聲干擾，造成磁道曲線突跳明顯且噪聲局部能量強，將正常磁場信號幾乎完全湮滅，且電道與磁道干擾出現的時刻具有一定的相關性[16]。這2類典型的強干擾噪聲大量出現在礦集區大地電磁測深數據中，得到的視電阻率曲線往往表現為明顯的近源效應。

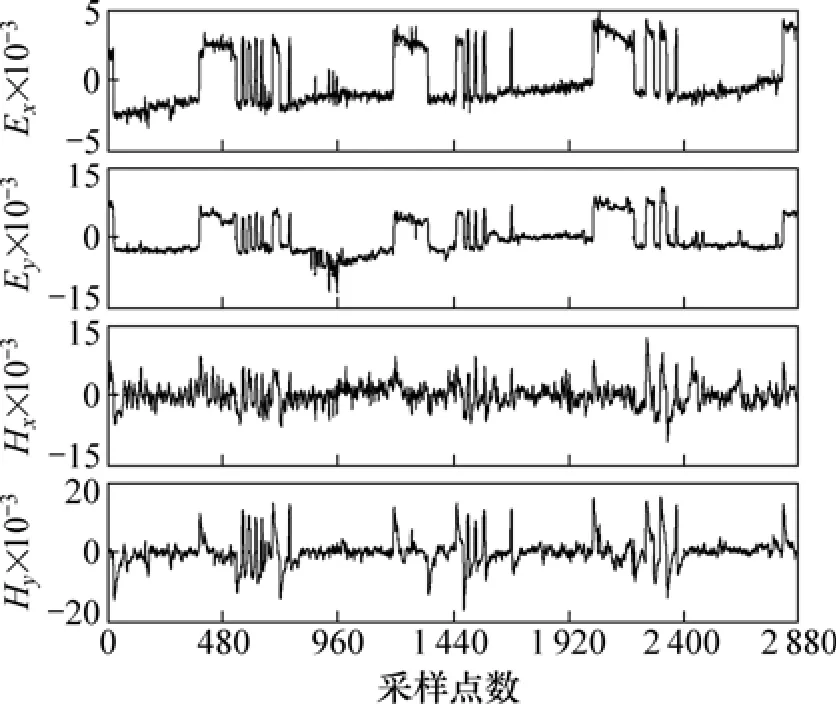
圖1 礦集區典型強干擾類型Fig.1 Typical strong interference types in ore district

3 數值仿真試驗

針對礦集區大地電磁信號的噪聲類型，模擬典型的含大尺度方波和充放電三角波的強干擾信號進行仿真試驗。根據形態濾波器的降噪性能，選擇不同的結構元素及尺寸進行分析。降噪性能評價標準采用濾波誤差E和信噪比RSN2組參數進行衡量，分別定義如下：

誤差E定義為：

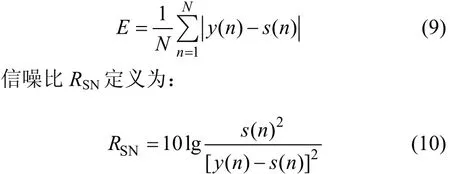
式中：s（n）為原始信號；y（n）為形態濾波輸出信號。

圖2所示為含大尺度方波的MT信號的形態濾波降噪效果。圖3所示為含大尺度充放電三角波的MT信號的形態濾波降噪效果。

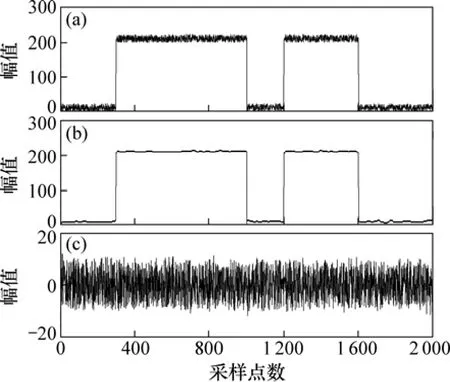
圖2 含大尺度方波的MT信號形態濾波效果圖Fig.2 Morphology filtering effect chart for large-scale square wave MT noise

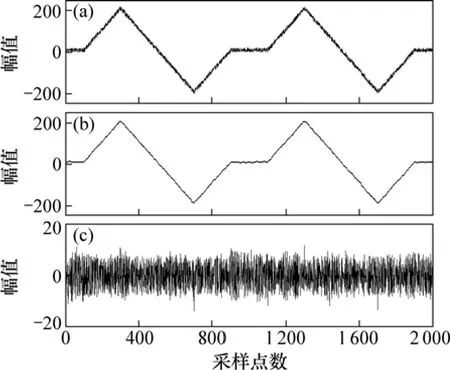
圖3 含大尺度充放電三角波的MT信號形態濾波效果圖Fig.3 Morphology filtering effect chart for large-scale charging and discharging triangle wave MT noise

由圖2和圖3可知：含大尺度方波和充放電三角波的大地電磁強干擾的能量幅值往往達到正常大地電磁信號的幾十倍，正常有用信號幾乎被完全湮沒。經形態濾波器后，提取出的形態輪廓清晰、平滑，幾乎完整地勾勒出含方波和充放電三角波的大尺度噪聲輪廓曲線，將小于或等于結構元素的信號濾除，只保留了比結構元素大的信號單元，重構后的大地電磁信號有效地剔除了疊加在有用信號上的大尺度干擾和由噪聲引起的突跳波形，抑制了基線漂移現象，凸出了大地電磁有用信號的相關局部特征，大尺度干擾與正常信號得到了有效分離。

表1和表2所示為含大尺度方波的MT信號采用不同結構元素及同一結構元素不同尺寸的濾波性能對比結果。

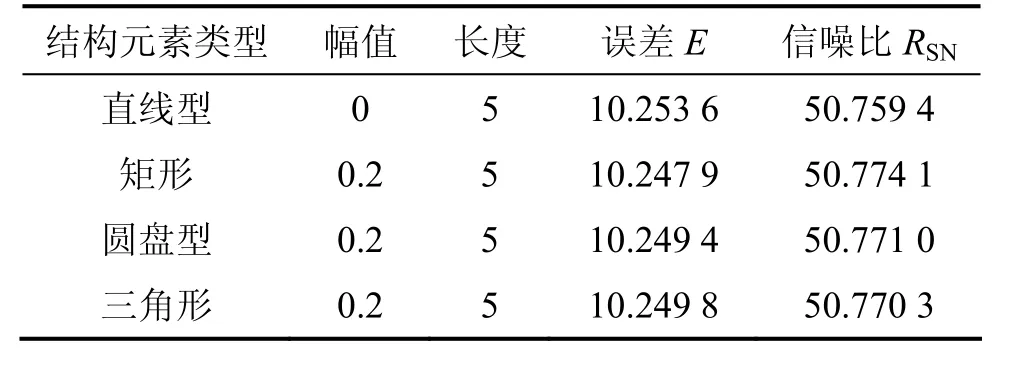
表1 含大尺度方波的MT信號采用不同結構元素濾波性能對比Table 1 Filtering performance comparison by different SEs for large-scale square wave MT noise

表2 含大尺度方波的MT信號采用不同尺寸的矩形結構元素濾波性能對比Table 2 Filtering performance comparison by different sizes of rectangular type SE for large-scale square wave MT noise

表3和表4所示為含大尺度充放電三角波的MT信號采用不同結構元素及同一結構元素不同尺寸的濾波性能對比結果。

結合濾波誤差E和信噪比RSN，分析表1～ 4的試驗結果可見：待處理信號的形狀與結構元素的形狀選取之間有一定的相似性，當電道中出現大尺度方波干擾時，選擇長度為15點和幅值為0.2的矩形結構元素的濾波效果較好，當磁道中出現大尺度充放電三角波干擾時，選擇長度為9點和幅值為0.2的三角形結構元素的濾波效果較好。而且，試驗發現：在選取結構元素的長度時，并不是結構元素的長度越長濾波效果就越好，當結構元素長度越長時，計算速度反而越慢。以上數值仿真試驗表明：數學形態濾波對大地電磁強干擾具有較好的去噪能力。

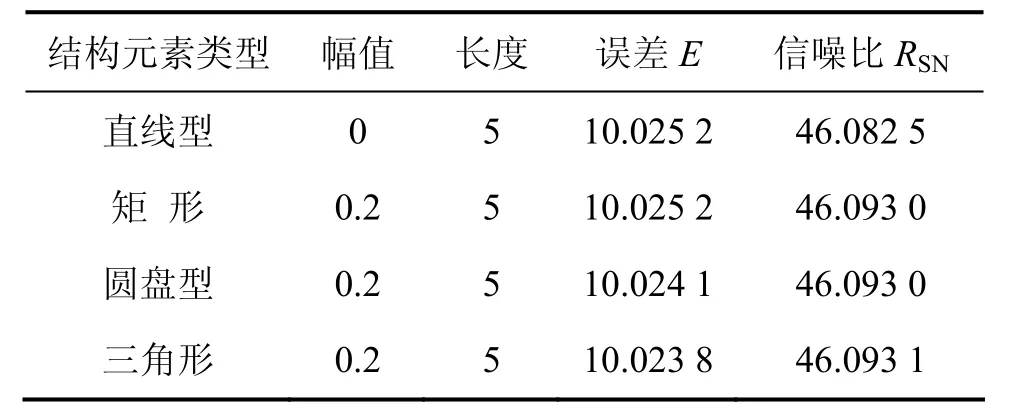
表3 含大尺度充放電三角波的MT信號采用不同結構元素濾波性能對比Table 3 Filtering performance comparison by different SEs for large-scale charging and discharging triangle wave MTnoise

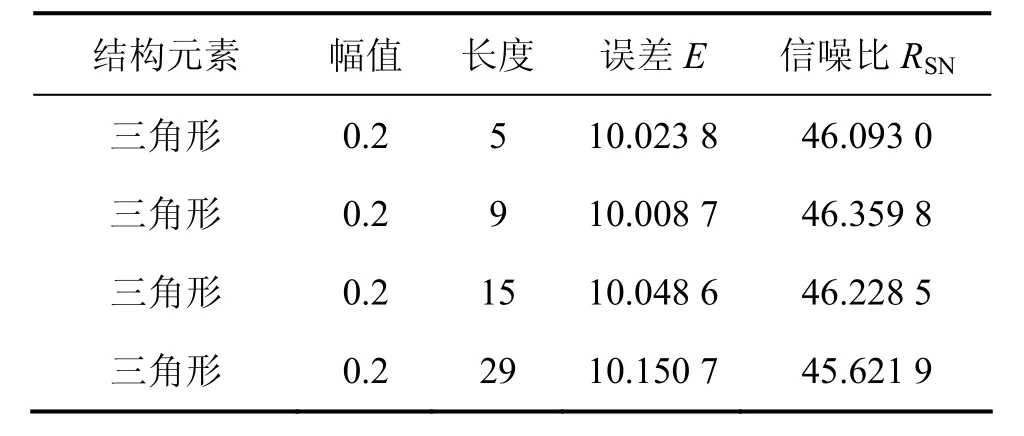
表4 含大尺度充放電三角波的MT信號采用不同尺寸的三角形結構元素濾波性能對比Table 4 Filtering performance comparison by different sizes of triangle type SE for large-scale charging and discharging triangle wave MT noise

4 實測資料應用

4.1 大地電磁信號數據提取

圖4（a）所示為該礦集區采集的實測大地電磁信號在Synchro Time Series View 中觀測到的Ex低頻段數據。V5-2000采集數據時在每個測點記錄Ex，Ey，Hx，Hy和Hz5個分量，并將原始數據記錄在TSH（高頻）和TSL（低頻）文件中。由于儀器不提供讀取時間序列的軟件，資料的處理相當于一個黑匣子。因此，首先必須獲取原始時間序列，才能進一步分析和處理大地電磁強噪聲干擾。

圖4（b）所示為根據V5-2000的數據采集格式[17]，在VC環境下進行編程，從TSH和TSL文件中讀取出的原始數據時間序列在Matlab中的觀測結果。對比圖4（a）和（b）可知：讀取的原始數據時間序列與儀器采集的數據一致，這樣就保證了后續資料處理的可靠性。

4.2 實測數據分析

鑒于大地電磁信號數據量龐大，僅選取其中1個測點4個分量（Ex，Ey，Hx和Hy）中的1個電場分量（Ex）和1個磁場分量（Hy）進行分析。

圖5所示為廬樅礦集區中某測點Ex信號經形態濾波后的去噪效果圖。

圖6所示為該測點Hy信號的去噪效果圖。

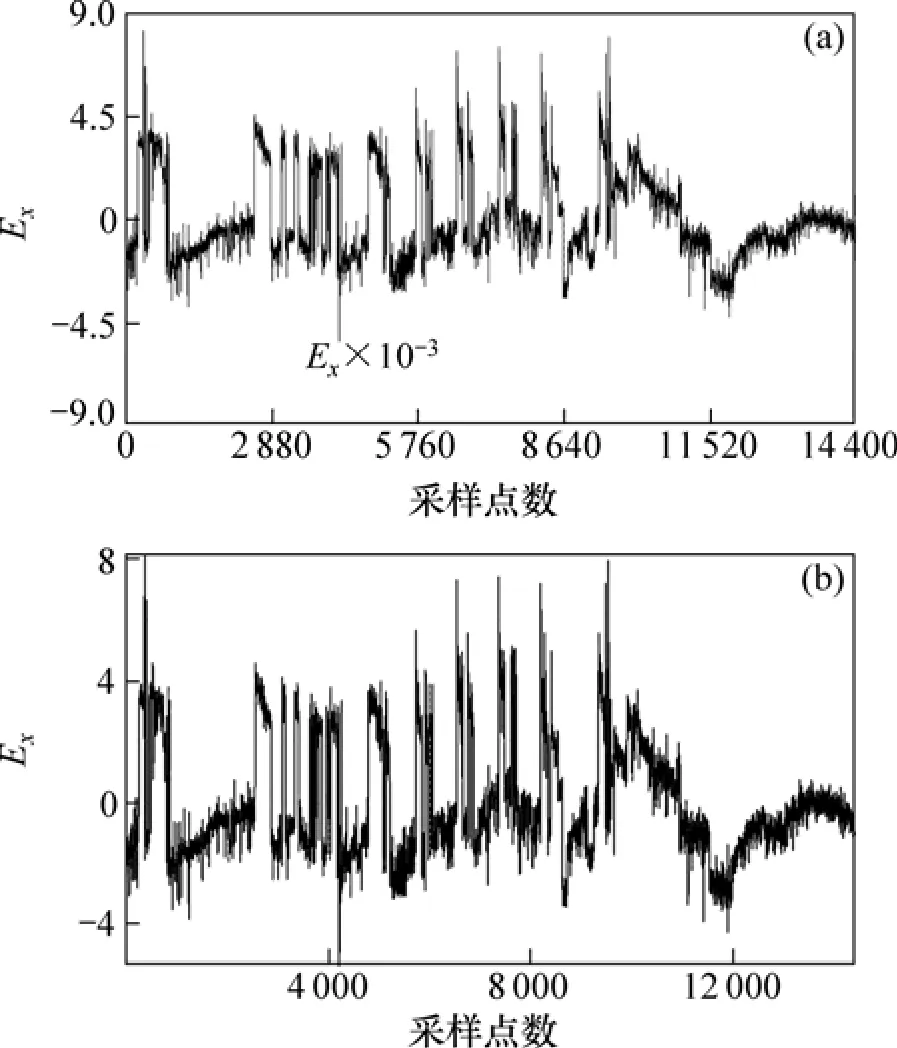
圖4 實測大地電磁測深數據Fig.4 Measured MT signal

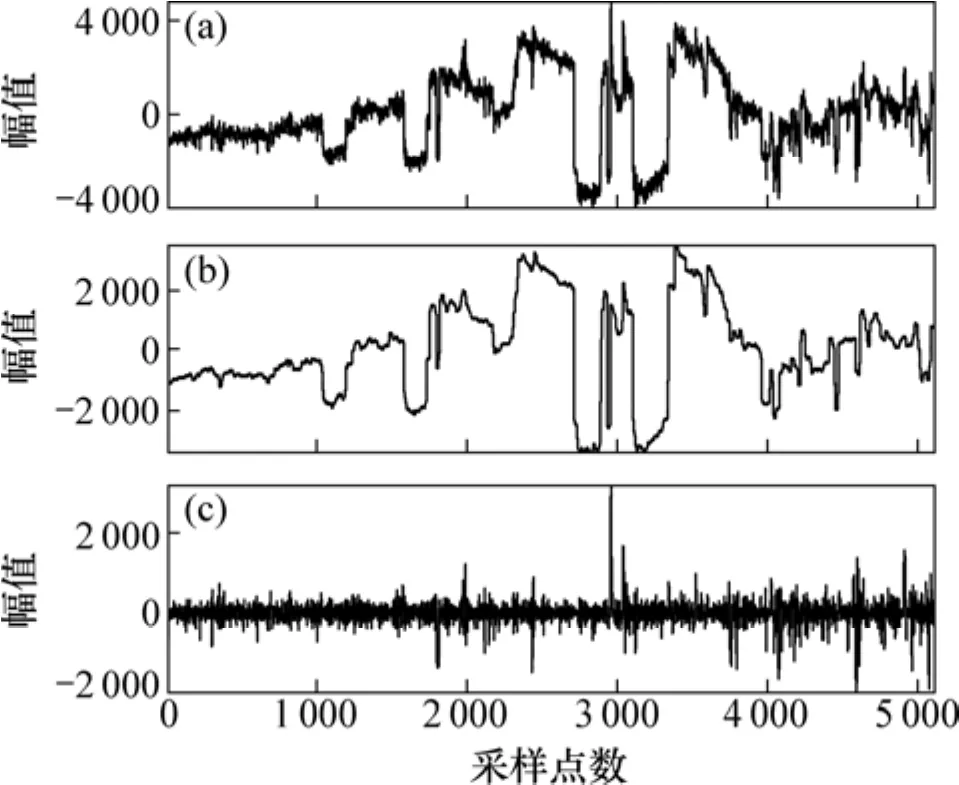
圖5 實測大地電磁信號Ex的去噪效果圖Fig.5 Morphology filtering effect chart for measured MT signal in Ex

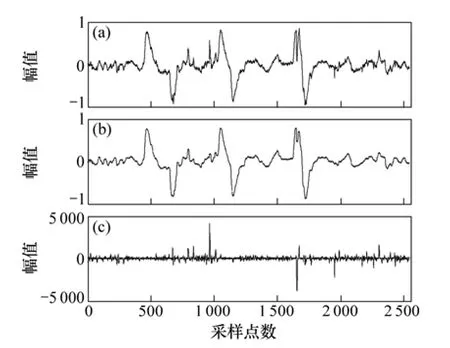
圖6 實測大地電磁信號Hy的去噪效果圖Fig.6 Morphology filtering effect chart for measured MT signal in Hy

分析圖5和圖6可知：含大尺度方波和充放電三角波的大地電磁強噪聲干擾經形態濾波后，提取出強干擾的大尺度形態輪廓，且曲線自然、光滑，較好地保持了原始信號的局部特征。重構后的大地電磁信號則基本去除了由噪聲引起的突跳波形，有效地抑制了大地電磁信號中的大尺度干擾和基線漂移，保留了較為豐富的細節成分，基本重現了大地電磁正常信號的原始特征。

圖7所示為廬樅礦集區某測線采用非線性共軛梯度法TE模式形態濾波前后的反演效果對比圖，圖8所示為采用非線性共軛梯度法TM模式形態濾波前后的反演效果對比圖。

分析圖7和圖8可知：形態濾波前后地下介質基本形態一致，形態濾波前由于個別測點受到近源干擾導致局部極值產生假高阻異常，從而影響周圍測點的反演結果，形態濾波后尖銳輪廓變得光滑，大大消除了近源干擾，從而使假高阻異常體減少，反演結果更加真實合理。

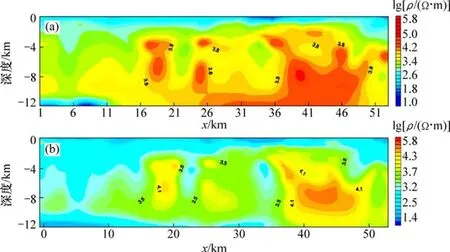
圖7 非線性共軛梯度法TE模式反演效果圖Fig.7 Nonlinear conjugate gradient method TE model inversion effect chart

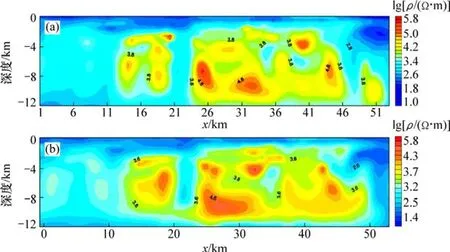
圖8 非線性共軛梯度法TM模式反演效果圖Fig.8 Nonlinear conjugate gradient method TM model inversion effect chart

5 結論

（1） 數學形態濾波能幾乎完整地勾勒出大地電磁強干擾中大尺度噪聲的形態輪廓，通過分析待處理信號的形態特征，合理地選取結構元素的類型和尺寸，能有效抑制大尺度干擾和基線漂移現象。

（2） 形態濾波法能較大改善礦集區大地電磁測深數據質量，對電磁法探測結果的處理和反演解釋具有重要意義。

（3） 數學形態濾波法原理簡單，具有并行運算速度快的優勢，適合于礦集區海量大地電磁強干擾分離，為提高大地電磁測深的深部探測能力提供了新的強有力的技術支持，應用前景廣闊。

[1] Cai J H, Tang J T. An analysis method for magnetotelluric data based on the Hilbert-Huang transform[J]. Exploration Geophysics, 2009, 40（2）：197?205.

[2] Trad D O, Travassos J M. Wavelet filtering of magnetotelluric data[J]. Geophysics, 2000, 65（2）： 482?491.

[3] 湯井田, 化希瑞, 曹哲民, 等. Hilbert-Huang變換與大地電磁噪聲壓制[J]. 地球物理學報, 2008, 51（2）： 603?610.

TANG Jing-tian, HUA Xi-rui, CAO Zhe-ming, et al. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese J Geophys, 2008, 51（2）： 603?610.

[4] Gamble T M, Gouban W M, Clarke J. Magnetotelluric with a remote magnetic reference[J]. Geophysics, 1979, 44： 53?68.

[5] Larsen J C, Maekie R L. Robust smooth magnetotelluric transfer functions[J]. Geophys J Int, 1996, 124： 801?819.

[6] 宋守根, 湯井田, 何繼善. 小波分析與電磁測深中靜態效應的識別、分離及壓制[J]. 地球物理學報, 1995, 38（1）：120?128.

SONG Shou-gen, TANG Jing-tian, HE Ji-shan. Wavelets analysis and the recognition, separation and removal of the static shift in electromagnetic soundings[J]. Chinese J Geophys, 1995, 38（1）： 120?128.

[7] 蔡劍華, 龔玉蓉, 王先春. 基于Hilbert-Huang變換的大地電磁測深數據處理[J]. 石油地球物理勘探, 2009, 44（5）： 617?621, 629.

CAI Jian-hua, GONG Yu-rong, WANG Xian-chun. Magnetotelluric data processing based on Hilbert-Huang transform in oil and gas exploration[J]. OGP, 2009, 44（5）： 617?621, 629.

[8] 范翠松. 礦集區強干擾大地電磁噪聲特點及去噪方法研究[D].長春： 吉林大學地球探測與科學技術學院, 2009： 43?55.

FAN Cui-song. The strong noise characteristics of MT in ore concentration area and research of denoise method[D]. Changchun： Jilin University. College of Geo-Exploration Science and Technology, 2009： 43?55.

[9] 張文斌, 楊辰龍, 周曉軍. 形態濾波方法在振動信號降噪中的應用[J]. 浙江大學學報： 工學版, 2009, 43（11）： 2096?2099.

ZHANG Wen-bin, YANG Chen-long, ZHOU Xiao-jun. Application of morphology filtering method in vibration signal de-noising[J]. Journal of Zhejiang University： Engineering Science, 2009, 43（11）： 2096?2099.

[10] 陳輝, 郭科, 胡英. 數學形態學在地震信號處理中的應用研究[J]. 地球物理學進展, 2009, 24（6）： 1995?2002.

CHEN Hui, GUO Ke, HU Ying. A study on application of mathematical morphology to seismic signal processing[J]. Progress in Geophys, 2009, 24（6）： 1995?2002.

[11] 岳蔚, 劉沛. 基于數學形態學消噪的電能質量擾動檢測方法[J]. 電力系統自動化，2002, 26（7）： 13?17.

YUE Wei, LIU Pei. Detection of power quality disturbances based on mathematical morphology filter[J]. Automation of Electric Power Systems, 2002, 26（7）： 13?17.

[12] Maragos P, Schafer R W. Morphological filters-Part I： Their set theoretic analysis and relation to linear shift invariant filters[J]. IEEE Trans on ASSP, 1987, 35（8）： 1153?1169.

[13] Maragos P, Schafer R W. Morphological filters-Part II： Their relation to median, order-statistic and stack filters[J]. IEEE Trans On ASSP, 1987, 35（8）： 1170-?1184.

[14] 趙靜, 何正友, 錢清泉. 利用廣義形態濾波與差分熵的電能質量擾動檢測[J]. 中國電機工程學報, 2009, 29（7）： 121?126.

ZHAO Jing, HE Zhen-you, QIAN Qing-quan. Detection of power quality disturbances utilizing generalized morphological filter and difference entropy[J]. Proceedings of the CSEE, 2009, 29（7）： 121?126.

[15] 張建成, 吳新杰. 形態濾波在實時信號處理中應用的研究[J].傳感技術學報, 2007, 20（4）： 828?831.

ZHANG Jian-cheng, WU Xin-jie. Research on applications of morphological filtering in real-time signal processing[J]. Chinese Journal of Sensors and Actuators, 2007, 20（4）： 828?831.

[16] 王大勇. 長江中下游礦集區綜合地質地球物理研究-以九瑞、銅陵礦集區為例[D]. 長春： 吉林大學地球探測與科學技術學院, 2010： 64?70.

WANG Da-yong. The integrated geophysical and geological study in the ore belt of the middle and lower reach of the Yangtze river-The cases study of Tongling and Jiurui ore district[D]. Changchun： Jilin University. College of Geo-Exploration Science and Technology, 2010： 64?70.

[17] 柳建新, 劉春明, 馬捷. V5-2000大地電磁測深儀文件頭數據格式研究[J]. 物探與化探計算技術, 2007, 29（4）： 359?362.

LIU Jian-xin, LIU Chun-ming, MA Jie. The data format of MT sounding instrument V5-2000[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2007, 29（4）： 359?362.

（編輯 何運斌）

Magnetotelluric sounding data strong interference
separation method based on mathematical morphology filtering

TANG Jing-tian, LI Jin, XIAO Xiao, XU Zhi-min, LI Hao, ZHANG Chi
（School of Geosciences and Info-Physics, Central South University, Changsha 410083, China）

Aimed at the problem that magnetotelluric signals are frequently influenced by strong noise interference during acquisition, a new magnteotelluric sounding data strong interference separation method based on mathematical morphology filtering was proposed. Firstly, the noise reduction capability was checked through simulated signal with the common strong interference and then the structure elements size selection program was analysed according to different noise types. Finally, the morphological filtering method was applied to the measured magnetotelluric signals noise reduction process. Experiments using nonlinear conjugate gradient method for inversion were conducted to check the improvement of magnetotelluric signals quality. The results indicate that the proposed method can effectively eliminate large scale disturbance and baseline drift of magnetotelluric signals. The method can better keep the original features of magnetotelluric signals, and the quality of magnteotelluric sounding data is improved. Because the principle of the method is simple and the parallel computing speed is fast, it has good application value and is suitable for the strong interference separation in ore district.

morphology filtering; magnetotelluric sounding; strong interference separation; structuring element

P631

A

1672?7207（2012）06?2215?07

2011?06?05；

2011?08?02

國家科技專項“深部探測技術與實驗研究專項”資助項目（SinoProbe-03）；國家自然科學基金資助項目（41104071）；湖南省教育廳資助項目（11B074）；中南大學中央高校基本科研業務費專項資金資助項目（2011QNZT012）

李晉（1981?），男，湖南衡東人；博士研究生，從事大地電磁強噪聲壓制及信號處理研究；電話：13574170783；E-mail：geologylj@163.com