一種鋼帶牽引并聯機構的機械結構設計

樊 銳，劉大為

（北京航空航天大學 機械工程及自動化學院，北京 100191）

半柔性冗余并聯機構由鋼帶牽引（steel-banddriven）介于剛性桿支撐并聯機構（strut-supported parallel mechanism）與柔性繩牽引并聯機構（wire-driven parallel mechanism）之間[1]。與伸縮桿式機構相比，鋼帶行程大，可增加機構工作空間，且整體質量小，可減小慣性；與繩牽引并聯機構相比，鋼帶的彈性變形較小，易于精確控制。另外，鋼帶寬度方向有一定的剛度，具有抗擾動能力，提高了動平臺位置精度和運動過程中的平穩性。因此，鋼帶式并聯機構，具有較好的工程應用前景。

本文介紹了一種立面1R2T（沿X、Y向移動、繞Z向轉動）鋼帶牽引并聯機構。以下就其設計進行分析。

1 理論分析

并聯機構處于奇異位形時，機構因失去剛度，而不可控，因此奇異性分析是設計和控制并聯機構的前提。

由于鋼帶只能受拉，所以其奇異性分析與繩牽引并聯機構類似。O.Ma給出了發生構型奇異的條件：

（1）如果動平臺和靜平臺是相似的正多邊形，則整個工作空間內雅戈比矩陣都是奇異的；

（2）如果動平臺和靜平臺是相似的非正多邊形，并且每一對相應的頂點通過一條連桿相連，則雅戈比矩陣JT非滿秩，在工作空間內的大部分區域都是奇異的[2]。

鋼帶牽引與繩牽引機構類似，借用繩牽引并聯機構可控工作空間的定義：

m條鋼帶牽引n自由度并聯機構，給定一個位姿X，如果作用在動平臺上外力螺旋（外力螺旋為穩定不變的力，如重力）向量WR∈Rn，各條鋼帶的拉力分布T∈Rm，滿足JTT=WR，且T＞0，則X屬于可控工作空間，這里m≥n+1，T=（t1，…，tm）T，JT靜力學雅克比矩陣（小節1.2將給出其計算過程）[3]。依據此定義，若并聯機構自由度為3，則至少需要4條鋼帶牽引，且鋼帶均受拉力，才能滿足工作空間內可控。

1.1 位姿求解

如圖1所示，

P(x，y，準)為動平臺中心點；

x，y分別為絕對坐標系下位置；

準為動平臺與水平面的夾角；

ki=表示驅動關節點Ai在固定坐標系{O}中的位置向量；

hi=表示從質心P到鋼帶與動平臺連接點Bi的向量；

Li=表示鋼帶的向量。

根據平面幾何的矢量封閉原理和坐標變換公式，模型中各向量滿足關系：

其中，X是從A1點到機構平面內P點的矢量。

式（1）中

將式（1）展開，可得第i根鋼帶的向量在X軸和Y軸上的投影向量：

而第i根鋼帶的長度可表示為

實際運動過程中，對于所需位姿(x，y，準)，通過式（3）求得鋼帶長度值，通過電機驅動鋼帶，達到動平臺位姿控制。

1.2 受力分析

動平臺所受的力和力矩如圖2所示。

圖2 動平臺受力簡圖

其靜力學方程為

ti為第i根鋼帶的拉力；

FR和MR分別為動平臺受到的穩定不變的外力和外力矩；

ui為沿鋼帶方向的單位向量

T 是 ti組成的向量（t1，t2，t3，t4）T；

WR=(FR，MR)T=(FRx，FRy，MRz)T是動平臺的力螺旋向量。

WR滿足關系：

式中，JT為靜力學雅克比矩陣：

JT矩陣是3×4的矩陣，由于其不是方陣，不存在逆陣，通過矩陣分析利用Moor-Penrose廣義逆（即偽逆矩陣），當已知動平臺所受外力，可得鋼帶拉力為

式中，

(JT)+為JT的Moore-Penrose廣義逆；

(JT)+WR為方程（7）的最小范數解；

Tnul為 JT矩陣零空間 N(JT)綴R4×1的一個分量，JTT的通解，即方程（7）的鋼帶拉力零空間解；

λ是一個不為0的比例系數，λ取值不同，式（5）求得鋼帶拉力也不同，但是通過對拉力零空間解的規劃，可以保證繩索拉力解的唯一性。

2 結構設計

理論計算時，將動平臺的位置與姿態離散，對應為一系列的鋼帶長度。動平臺由一個姿態到另一姿態，是通過不同的鋼帶長度組合得到的[4]。

鋼帶的纏繞方式有單層和多層纏繞，如圖3所示。

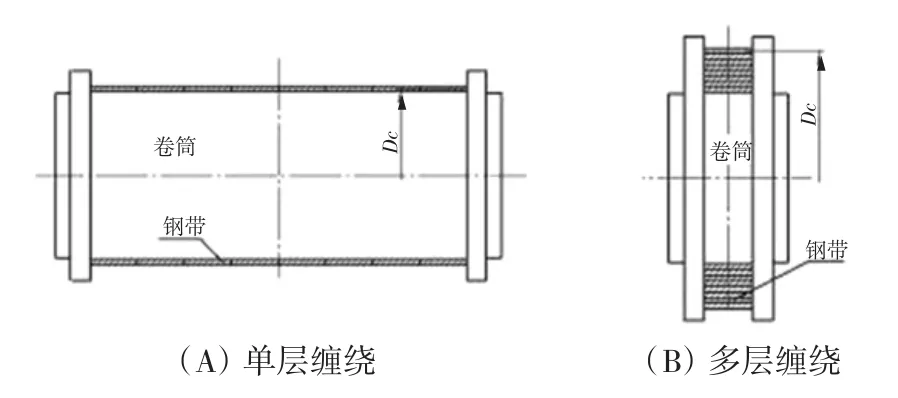
圖3 鋼帶卷繞方式

由于鋼帶有一定厚度，采用（B）方式時彎曲應力比（A）大，節省空間。

但從控制角度看，（B）方式中鋼帶中心處直徑Dc在卷繞過程中，一直都在變化，若編碼器與卷筒同軸，難以獲得等量反饋脈沖數。若將編碼器與卷筒分離，則可解決這個問題。

平面三自由度并聯機構，需要有4根鋼帶牽引，才能完成控制。4個驅動單體放置在靜平臺四角：以Ai（i=1，2，3，4）點作為出帶點。Ai點在驅動單體的一側中心線上。單體的結構布局與繞帶方式都完全相同，實現了模塊化設計。

單體主要由電機輪、測長輪和測力輪等部分組成，如圖4所示。

圖4 驅動單體機構簡圖

電機輪包括卷筒和帶電機。張力傳感器實現鋼帶內張力的測量。編碼器，用來測量放出或收回鋼帶的長度，壓緊輪保證鋼帶與碼盤輪貼緊。兩個出線過輪的切點在中心線上，保證出帶位置不變。

若將動平臺設計成正方形，則靜平臺必須是非正方形，否則會產生奇異。此時1R2T并聯機構工作空間內都有rank（JT）=rmax=3，因此機構中無奇異狀態。

3 精度分析

動平臺的位姿精度，主要受到以下因素影響：

（1）碼盤測量精度；

（2）載荷作用下，鋼帶變形；

（3）出帶點位置誤差。

對于（1）和（3），采用壓緊輪可避免鋼帶打滑，在制造時嚴格控制裝配定位關系，該誤差是系統誤差，可通過標定來補償。

本樣機鋼帶彈性模量為200 GPa，截面積A=10 mm×0.2 mm=2 mm2，靜平臺長寬分別為997 mm和846 mm，動平臺總質量24 g。

所以外力螺旋 WR=[0，-0.24，0]T

將式（7）通過MATLAB編程，求得空間內最大受力30 N，此時鋼帶長l=791mm。

根據材料力學計算，鋼帶受力時伸長量

對動平臺運動精度的影響不大。

4 相關實驗

為考察驅動單體的運行精度和重復性，進行了驅動單體帶50 N負載時，運行位置精度測試實驗。圖5所示為實驗流程及實驗現場。

圖5 實驗原理及實驗系統

閉環控制鋼帶伸縮量，重復收放行程，記錄動平臺的位移量，與理論值作比較。結果見表1。

表1 驅動單體位置精度測試表1 (單位：mm)

可以看出，在鋼帶收放時，存在誤差，這主要與負載重力和電機停轉時電壓有關。這是因為PMAC輸出停轉指令后，由于慣性作用，電機仍然具有瞬時速度。停轉電壓越大，慣性越大，誤差越大；而放鋼帶時，受負載重力的影響，誤差更大。可減小負載，并通過實驗測得電機收鋼帶時負載的最小電壓，通過降低停轉電壓，減小加減速度。通過這種方法可有效減小了誤差。表2為改善實驗方法后鋼帶長度變化情況。

表2 驅動單體位置精度測試表2 (單位：mm)

在驅動單體標定實驗的基礎上，進行了鋼帶牽引機構無旋轉的單方向運動控制實驗，如圖6所示。

圖6 動平臺牽引實驗系統

圖 7以 準=0°，由點（301，153） 運動到點（351，153）時，動平臺實際運動位姿與理論值的對比結果。X、Y最大誤差分別為1.2 mm和1 mm，最大轉角誤差為0.12 rad。

誤差產生的原因主要有：

（1）零點及方向位置點坐標準確測量；

（2）脈沖當量標定；

（3）控制算法等。

這些都是后續工作的內容。

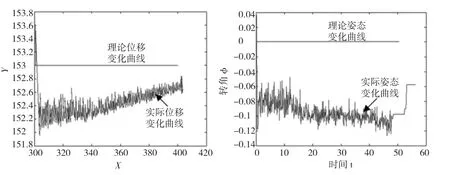
圖7 動平臺位姿變化曲線

5 結束語

本文介紹了立面1R2T鋼帶牽引并聯機構的初步研究成果。通過對機構奇異性和可控性的分析，可以得到機構可控和不發生奇異的條件，以及鋼帶張力變化規律，明確結構設計應注意的問題，經實驗標定掌握單體控制精度，機構動平臺的運動控制，實驗證明了理論分析及結構設計的合理性，為鋼帶牽引并聯機構的進一步研究打下了基礎。

[1]鄭亞青，劉雄偉.繩牽引并聯機構的研究概況與發展趨勢[J].中國機械工程，2003，14(9)：808-810.

[2]趙 澤.大射電望遠鏡懸索饋源支撐系統的機械結構設計與分析[D].西安：西安電子科技大學，2003.