基于神經網絡和遺傳算法的衛星結構參數優化

韓 沖，陳 慶

（上海空間推進研究所，上海 200233）

對于衛星產品，追求更小的結構總質量和較高的一階固有頻率，一直是科技人員追求的目標。為了減輕衛星結構的總質量，通常有兩種途徑：一是對衛星結構進行優化設計；二是采用比模量和比強度高的復合材料代替傳統的金屬材料。

在復合材料工藝水平確定的情況下，優化設計顯得尤為重要。在結構優化中，傳統的有限元方法是重要方法之一。但是傳統優化計算效率較低，優化過程參與了大量的有限元計算，耗時較多。如果變量設置不合理，往往陷入局部最優解的困境。

像整星結構這類單元較多的復雜結構，若直接采用商業軟件進行優化，大量工作花費在了對分析文件的提取過程。如果是不熟悉軟件語言的初學人員，將會遇到很大的挑戰。因此需要探索新的優化方法，來完成優化工作。

本文嘗試建立整星結構一階固有頻率最大、質量最小為目標的多目標優化設計模型，采用線性加權的方法，將多目標優化問題轉換為單目標優化問題。結合正交實驗技術，采用神經網絡和遺傳算法，在MATLAB軟件平臺上，完成整星結構的優化計算。

1 神經網絡和遺傳算法

1.1 神經網絡

人工神經網絡（Artificial Neural Networks，ANN），簡稱神經網絡，作為對人腦最簡單的一種抽象和模擬，是近年發展起來的一門十分活躍的交叉學科。理論證明，三層BP網絡能映射任意的非線性函數，并且具有較好的全局收斂性與結構簡單等優點。而針對衛星結構的設計參數與其固有頻率的關系，亦是非線性關系，因此采用BP網絡來映射從設計變量到目標函數的非線性關系，是比較合理的。圖1所示為三層BP網絡結構模型。

圖1 三層BP網絡示意圖

1.2 遺傳算法

遺傳算法通過模擬自然界生物的進化過程來進行擇優。其從代表問題的可能潛在解集的一個種群開始，而一個種群則是由經過基因編碼的一定數目的個體組成。每個個體，實際上是染色體帶有特征的實體。染色體作為遺傳物質的主要載體，即多個基因的集合，其內部表現是某種基因組合，其決定了個體的外部表現。

在初始種群產生之后，按照適者生存和優勝劣汰的原理，逐代演化產生出越來越好的近似解。在每一代，根據問題域中個體的適應度大小挑選個體，并借助于自然遺傳學的遺傳算子進行組合交叉和變異，產生出代表新的解集的種群。這個過程導致種群像自然進化一樣，后生代種群比前代種群更適應于環境，末代種群中的最優個體經過解碼，可以作為問題的近似最優解。

遺傳算法計算過程的實現，主要取決于變量編碼、初始群體生成、適應度函數設計、遺傳算子設計、算法控制參數選取、算法停止準則等環節設計。遺傳算法流程圖如圖2所示。

圖2 遺傳算法流程圖

2 應用與分析

2.1 優化模型

圖3所示為某衛星結構圖。

圖3 衛星結構圖

下面就是衛星整星結構多目標優化設計數學模型的目標函數：

式（1）中的 12 個自變量 x1，x2，…，x12表示相應的獨立設計變量。

衛星整星結構優化模型可以描述如下：

式（2）中，

W為衛星結構總質量；

freq1是衛星結構一階固有頻率；

Tdi和T蜂窩芯分別對應蜂窩夾層板和蜂窩芯的失效公式；

umax為結構過載工況下的最大位移；

Mmax為相應材料的應力值；

Hi為蜂窩芯的厚度；

Lp為面板的厚度；

Rq為構架圓管的半徑；

u0、M0和f0分別為衛星結構的各許用值。

2.2 優化設計變量參數組合表形成

本文的優化問題所涉及的參數和各參數的水平數不是太多，并且要將這些參數組合的計算結果，用于神經網絡的訓練。因此，參數的組合不能太少，并且要能反映出各個參數對計算結果的影響規律，本文采用正交實驗選參法。各優化設計變量的水平數如下：

底板蜂窩芯子高度Hd：10～60 mm，在其變化范圍內取6個水平數，增量為10 mm；

底板面板厚度Ld：0.2～1.0 mm，在其變化范圍內取9個平均數，增量為0.1 mm；

層板蜂窩芯子高度Hc：10～60 mm，在其變化范圍內取6個平均數，增量為10 mm；

層板面板厚度Lc：0.2～1.0 mm，在其變化范圍內取9個平均數，增量為0.1 mm；

長立板蜂窩芯子高度Hl：10～60 mm，在其變化范圍內取6個平均數，增量為10 mm；

長立板面板厚度Ll：0.2～1.0 mm，在其變化范圍內取9個平均數，增量為0.1 mm；

其余結構板蜂窩芯子高度Hj：10～60 mm，在其變化范圍內取6個平均數，增量為10 mm；

結構板面板厚度Lj：0.2～1.0 mm，在其變化范圍內取9個平均數，增量為0.1 mm；

承力筒蜂窩芯子高度Ht：10～60 mm，在其變化范圍內取6個平均數，增量為10 mm；

承力筒單層面板厚度Lt：0.01～1.0 mm，在其變化范圍內取9個平均數，增量為0.1 mm。

從上述設置的水平數可以看出，蜂窩芯子高度的水平數比其他變量的水平數小，為方便使用正交實驗表進行參數組合，采用擬水平法將所有的設計變量的水平數統一為9個。對于蜂窩芯子高度增補的水平數分別是50 mm，40 mm，30 mm。最后參考10個變量，9個水平數的正交設計表，得到如表1所示的參數組合表。挑選出符合實際結構要求與滿足強度要求的參數組進行固有頻率與質量的計算，為神經網絡的訓練提供樣本。

表1 基于正交實驗法的各設計變量的參數組合（部分）

在表1中最后一列“驗證”，表示對相應的參數組進行衛星結構的靜力計算與校核。Y表示滿足結構的強度要求和位移要求，N表示不能滿足相應的要求。

通過對表1中滿足靜力要求的參數組進行衛星固有特性計算，獲得相應參數組合的計算結果。為了提高計算效率，本文采用Power dynamics方法進行低階頻率計算（如表2所列）。

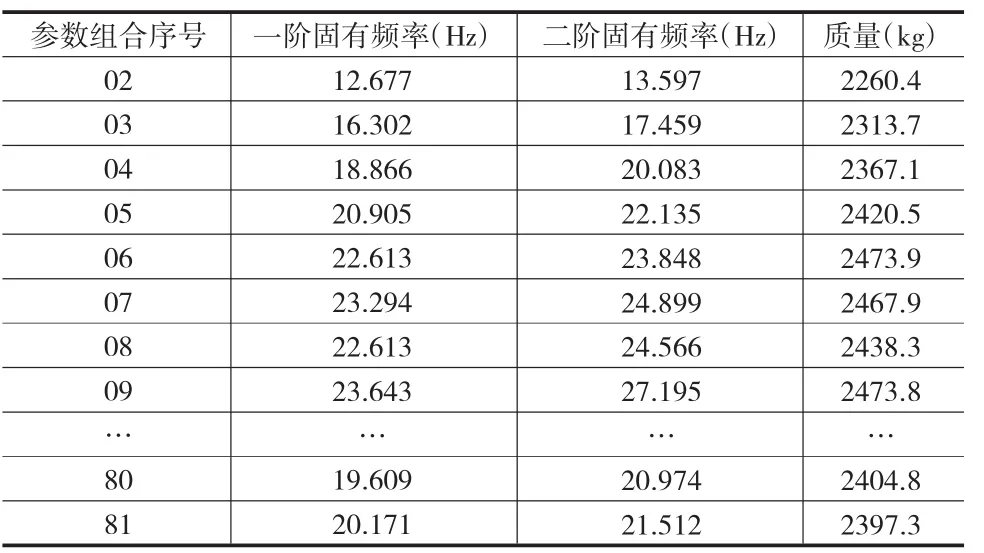
表2 各設計變量參數組對應的計算結果（部分）

2.3 神經網絡和遺傳算法程序編寫

在MATLAB7.0軟件平臺基礎上，應用神經網絡工具箱中的函數，編寫針對已有樣本的神經網絡程序，并對訓練好的神經網絡進行樣本的檢驗，直到滿足所有檢驗樣本對應的目標值均在許可的范圍內為止。

神經網絡的結構參數如下：

BP網絡，30個隱含層，10個輸入變量，2個輸出變量；

輸入層轉移函數為tansig，隱含層轉移函數為logsig函數，輸出層轉移函數采用線性purelin函數，訓練函數采用trainlm函數；

初始權系數值由系統的隨機函數自動給出，取最大訓練步數為5 000步，目標誤差精度為1e-4，學習率為0.15；

直到達到訓練所要求最大訓練步數或目標誤差精度為止。

MATLAB7.0中的主程序片段如表3所示。

表3 神經網絡主程序片段

在神經網絡的訓練程序中，將輸入輸出樣本值存儲起來，以備后來編寫遺傳算法程序中所用。神經網絡訓練過程中，誤差的精度和訓練步數的關系圖見圖4。

圖4 神經網絡訓練誤差和迭代關系曲線圖

從誤差曲線看出，訓練過程約經過1 300步達到誤差精度要求。通過對樣本的仿真值的檢驗，發現訓練好的網絡泛化能力較強，能夠到達預期效果。因此，該神經網絡的結構是合理的。

首先根據神經網絡的訓練結果，在MATLAB7.0軟件平臺上進行目標函數的多項式擬合。考慮到以一階頻率最大和總質量最小的雙目標優化，可以利用加權系數將其轉化為單目標優化工作。具體如式（3）。

式（3）中，

w1、w2分別為整星結構質量和一階頻率的加權值；

W、F分別為整星結構質量和一階頻率。

根據要求不同，可以設置不同的w1、w2。本章取值：w1=0.4，w2=0.6。

W、F分別除以kg、乘以100/Hz來實現無量綱化。

最終得到以各結構參數為自變量的多項式：

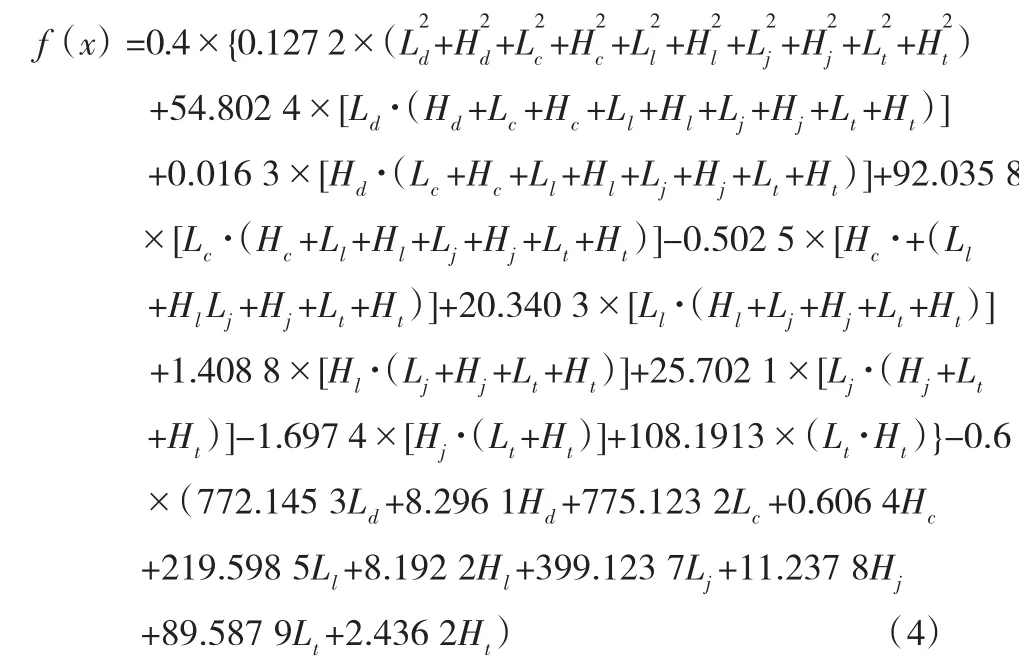
在MATLAB7.0環境下，編制遺傳算法主程序及各個相應子程序。設置種群大小為80，交叉概率為0.9，變異概率為0.001，計算代數為200。（見表4）。

表4 遺傳算法主程序片段

2.4 優化結果分析

調試并運行程序，得到遺傳代數與最佳適應度值變化關系（如圖5所示）。

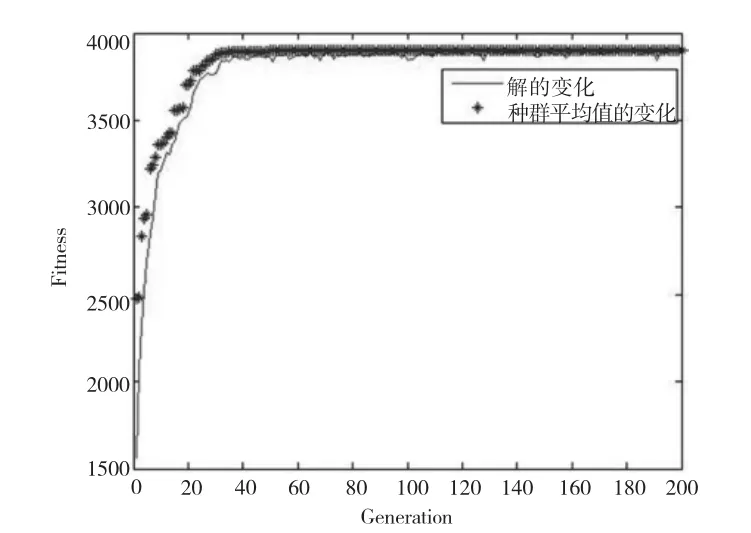
圖5 遺傳代數與最佳適應度值和平均適應度值的關系

對應的自變量參數值見表5。

表5 優化后得到的設計變量值 （單位：mm）

經過驗證，表5所示的參數組滿足結構的靜力強度要求。對應這組參數的ANSYS計算結果為：一階固有頻率為16.647 Hz，質量為2 314.4 kg。可以認為表5的變量值即為結構設計變量的全局優化值。

使用商業軟件ANSYS優化模塊，按照傳統優化方法的優化結果見表6。

表6 使用傳統優化方法的優化結果 （單位：mm）

對應于該參數變量值下的整星結構質量是2306.3 kg，一階固有頻率為14.624 Hz。

比較兩種方法的優化結果，使用神經網絡結果遺傳算法的結構優化設計方法，盡管得到了較大的整星質量，但是在一階固有頻率上有明顯的優勢。

3 結束語

本文針對衛星結構的多目標優化設計模型，在MATLAB7.0軟件平臺的基礎上，通過BP網絡結合遺傳算法，完成了一階固有頻率最大、質量最小的多目標優化計算，得到了比較合理的設計變量值。驗證了BP網絡結合遺傳算法在衛星結構優化中的可行性。

筆者將商業軟件ANSYS優化模塊的優化工作和本文的優化工作對比，得出前者的主要工作是分析文件建立，耗時最多的是迭代過程；后者的主要工作是BP網絡的建立和遺傳算法的編寫，耗時最多的是各正交實驗參數下結構計算。在當今MATLAB軟件各種工具箱相對完善的情況下，采用后者對復雜結構進行優化計算會更簡潔，更省時。

[1]燕樂緯.基于遺傳算法的結構動力優化[D].重慶：重慶大學，2006.

[2]吳仕勇.基于數值計算方法的BP神經網絡及遺傳算法的優化研究[D].昆明：云南師范大學，2006.

[3]Surrry，et al.“A Muti-objective Approach to Constrained Optimization of Gas Supply”[R].Networks.AISBEC,Sheffield,1995.Volume 993/1995,166-180.

[4]Whiltey D.“Modeling Hybrid Genetic Algorithms”[R].In:Genetic Algorithm in Engineering and Computer Science,Winter G(ed).Wiley,1995.

[5]蔣良孝，李超群.基于BP神經網絡的函數逼近方法及其MATLAB 實現[J].微機與應用，2004，(1)：52-53.

[6]楊雁寧.利用MATLAB實現BP神經網絡的設計[J].河南科技，2005，(8)：46-47.

[7]劉 強，譚光宇，等.基于遺傳算法的復雜槽型銑刀片槽型參數優化[J].工具技術，2007，（41）：11-14.