風場環境下主動建模無人直升機改進LQG控制

李一波，劉婉竹，宋崎，2，趙樹

(1.沈陽航空航天大學自動化學院，遼寧沈陽 110136;2.沈陽自動化研究所第一研究室，遼寧沈陽 110016;3.中航工業西安飛機工業(集團)有限責任公司 第31廠，陜西 西安 710089)

引言

無論是高大建筑物的屋頂平臺，還是高山峽谷的狹小平地，小型無人直升機均能起降自如，實施多種作業。這樣一來就使得執行任務的環境信息常常是不完全透明的，文獻［1］把這種信息不完全透明的環境稱作不確定環境。目前國內外對于無人直升機飛行控制系統的研究，尤其是對于不確定環境下的研究還不是很充分，主要有以下幾種［2］:(1)用特征結構配置法;(2)定量反饋理論(QFT);(3)H∞控制;(4)線性二次型高斯/傳遞回路恢復(LQG/LTR)方法。LQG方法是用來處理有隨機噪聲干擾或模型狀態無法直接測量情況下的狀態反饋最優化設計方法［3］，其本質是附帶卡爾曼濾波器的最優二次型控制器。由于傳統的LQG控制方法只能對模型中的狀態進行估計，而主動建模技術可以對模型中的參數和狀態進行在線估計［4］，因此本文將主動建模技術與傳統的LQG控制相結合，為系統實時地建立相對準確的模型。

本文所考慮的不確定環境主要指風場環境。在飛行控制系統設計中，大氣擾動的各種參數(如風速、風向等)是變化的，當風速非常大，與飛行器的飛行速度接近一個數量級時，大氣擾動不能再被看作小擾動事件，為了對飛行器進行有效控制，需要獲知大氣擾動的模型。大氣擾動表現為變化風，其對飛行器的影響主要有風切變和大氣紊流［5］。其中大氣紊流是一種隨機現象，通過抑制紊流干擾改善飛行品質，提高飛行器性能。

目前大氣紊流模型有Dryden模型和Von Karman模型，但二者的建模理論體系卻截然相反［6］。本文采用改進的Von Karman模型，即對該模型進行有理化逼近，直接基于簡化的模型生成大氣紊流。

1 直升機半解耦模型的建立

直升機的全狀態空間模型包括直升機的剛體動力學模型、旋翼和機身耦合模型、旋翼穩定桿的耦合模型、航向增穩回路模型［7］。

由于直升機全狀態空間模型含有耦合參數，且有13個狀態量和4個控制輸入量，為了簡化計算和便于穩定性分析，將縱向和橫向的耦合參數設為零，并加入一些自由控制參數以補償耦合動力學模型，這樣得到半解耦之后的3個運動方程:縱向運動方程、橫向運動方程和航向運動方程［8］。表達式如下:

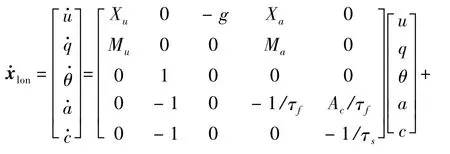
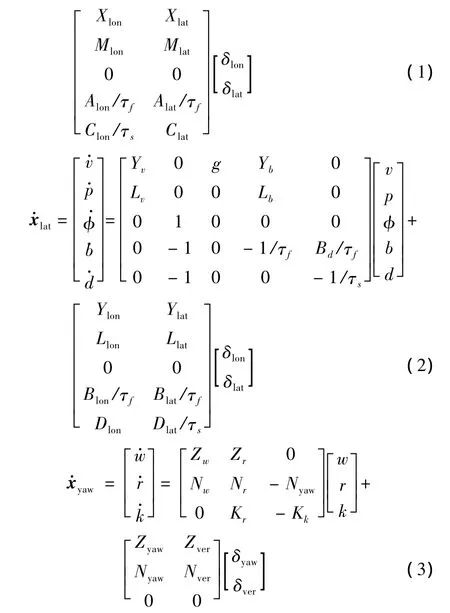
2 風場模型的建立

2.1 大氣紊流的模型

自然界中的風從來不以純凈的形式出現，由于摩擦、旋渦等原因，在風出現的同時，也往往伴有紊流。大氣紊流現象的形式和出現與很多因素有關，例如風切變、熱交換、地形誘導等。大氣紊流可以看作是疊加在常值風上的連續隨機脈沖。通常認為紊流是一種平穩、均勻、各態遍歷及各向同性的隨機過程。該過程的統計特性不隨時間變化。由于Von Karman模型的使用較廣泛，所以本節針對該模型進行介紹。

Von Karman模型的能量頻譜函數為:

2.2 數值仿真實現

由于得到的Von Karman模型在飛行仿真實驗中不能直接使用，所以首先進行共軛分解，而后使用有理化的方法將其簡化，形式如下:

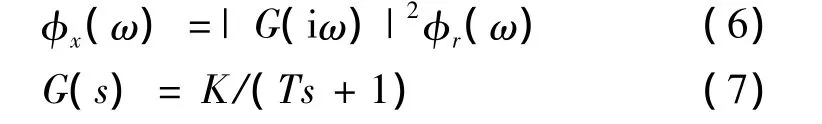
用簡化后的Von Karman模型進行數值仿真時，將計算機產生的隨機信號作為輸入端的信號源，而后將其送入到已按給定頻譜設計好的濾波器中，在線實時生成仿真中所需要的大氣紊流數據。本文通過計算機產生的隨機信號是均值為零、方差為1的高斯白噪聲。

在計算機仿真中所用到的遞推公式為:

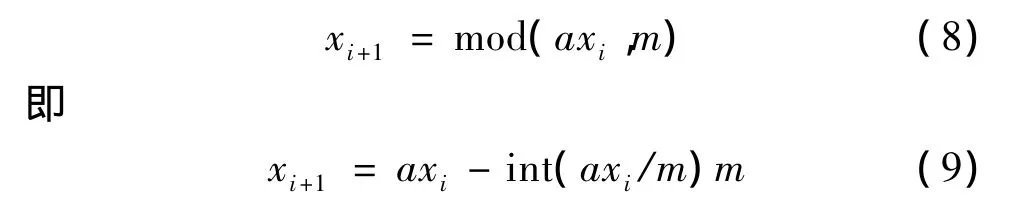
在飛行實時仿真中，以h為步長(即采樣周期)將成形濾波器的傳遞函數G(s)離散化，生成x(t)離散序列的歐拉前差分公式為［9］:

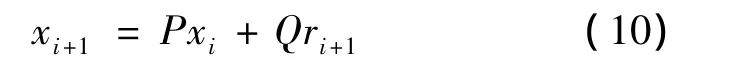
式中，xi為離散序列x第i點的值，即當t=ih時的x值;ri+1為高斯白噪聲序列;P和Q與采樣周期有關，為待定系數。

按式(10)不斷遞推產生大氣紊流隨機信號x(t)，從而實現在線實時仿真。

3 基于主動建模的改進LQG控制

3.1 LQG控制

3.1.1 LQG 介紹

LQG控制方法采用卡爾曼濾波估計狀態，并采用線性二次型控制器來設計反饋調節器，它常用來處理有隨機噪聲干擾存在的或模型狀態無法直接測量的控制系統，這樣能夠保證系統的魯棒性能。

一個典型的LQG控制系統如圖1所示，其中控制器Gc就包含了待設計的卡爾曼濾波器和二次型補償器。

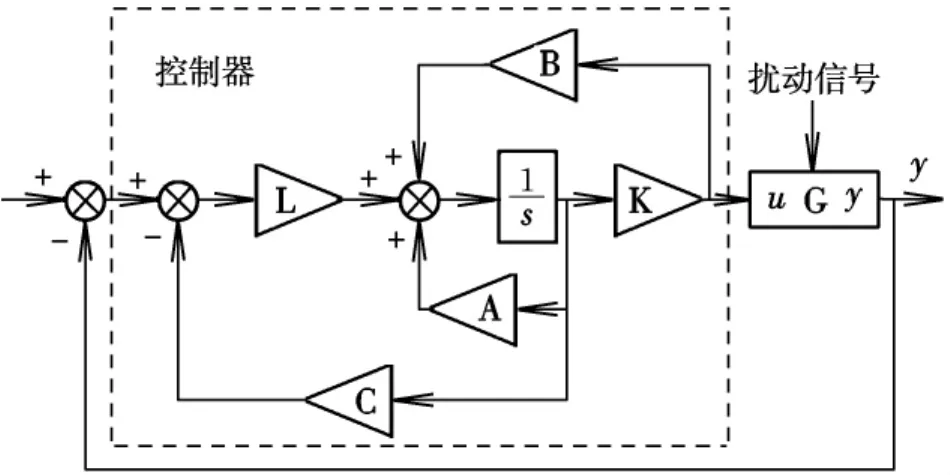
圖1 典型的LQG控制系統

3.1.2 LQG 設計

設控制系統的方程有如下表達式:

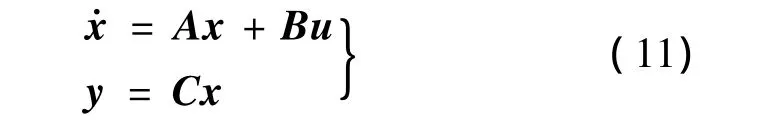
式中，x為飛行器的狀態量;u為控制輸入量。如果用z表示期望輸出量，則誤差量可表示為:

LQR的設計方法可描述為:首先確定飛行器期望的時域性能指標，并以二次型的形式定義狀態調節性能指標J，即:

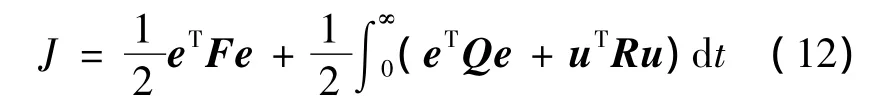
設計反饋調節器K，使式(12)最小，并保證所用的控制能量以及飛行器狀態的振蕩最小。

3.1.3卡爾曼濾波

為了克服數據無法處理的問題，20世紀60年代卡爾曼將狀態空間模型引入到濾波理論中，推導出了一套遞推估計算法，后人稱之為“卡爾曼濾波理論”。卡爾曼濾波器采用含有噪聲的系統信號狀態空間模型，利用當前時刻的觀測值和上一時刻的估計值來更新對狀態變量的估計，從而求出當前時刻的估計值。

設隨機線性離散系統的方程為:

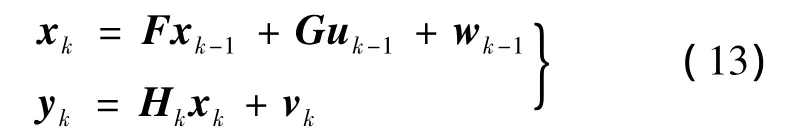
式中，xk，yk和 uk－1分別為狀態量、觀測量和輸入量;F為狀態轉移矩陣;G為輸入轉移矩陣;wk－1為系統過程噪聲矩陣;Hk為測量矩陣;vk為測量噪聲矩陣。其算法流程如圖2所示。

圖2 卡爾曼濾波算法流程

3.2 基于主動建模的改進LQG控制

3.2.1聯合估計

主動建模是指在對模型中的狀態進行估計時采用在線估計的方法，為系統實時地建立相對準確的模型。設含有時變參數的離散系統狀態空間方程

如下:

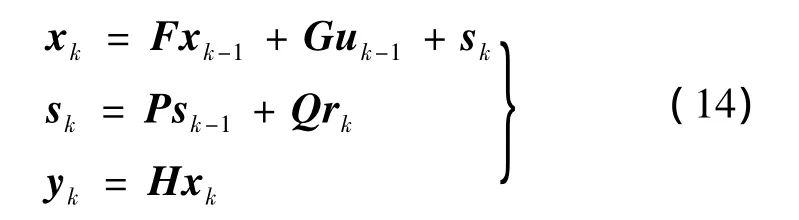
式中，xk為狀態量;sk為時變參數。

若在估計式(14)中xk與sk的值時采用了同一種估計算法，則這種估計方法就稱為“聯合估計”。為了便于估計將式(14)中的xk與sk組合在一起成為增廣的狀態量，即 x'k=［xk，sk］，那么式(14)可寫為如下的形式:

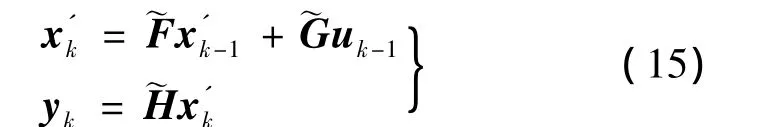
用卡爾曼濾波估計算法對式(15)中的x'k進行估計，從得到的增廣狀態量估計結果中即可得到時變參數的估計值。

3.2.2控制器重構

將風擾動的估計值反饋給控制器，實現控制器的重構，從而實現有效控制。圖3給出了控制器重構的原理示意圖。

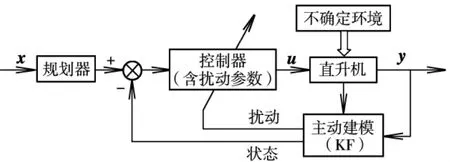
圖3 控制器重構原理

4 仿真實驗

4.1 縱向仿真

文獻［8］中給出了縱向運動方程中參數數值的大小，將其帶入式(1)后得到下列矩陣:

通過矩陣A求得縱向運動方程的零極點，如圖4所示。

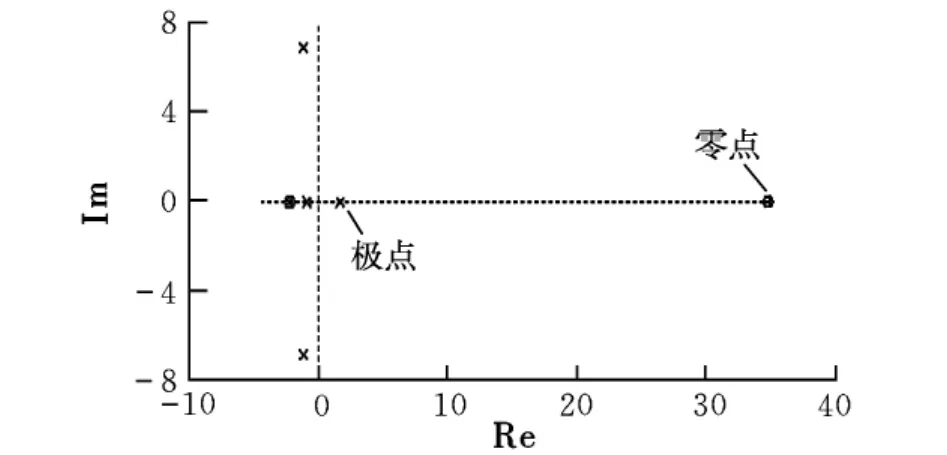
圖4 縱向運動方程的零極點圖

從圖4可以看出，有一個零點和一個極點位于s復平面的右半平面，說明系統是不穩定的。經過多次反復的試驗，得到LQR控制器中的q和r的參數取值如下:

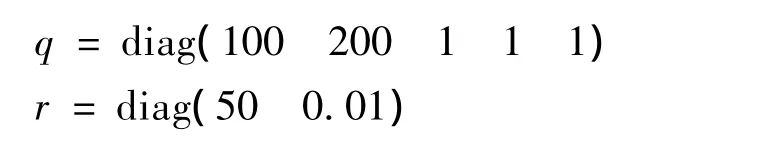
當直升機處于大氣紊流場中時，紊流的大小和方向是未知的，可由式(10)仿真得到。圖5給出了卡爾曼濾波對大氣紊流的估計結果。

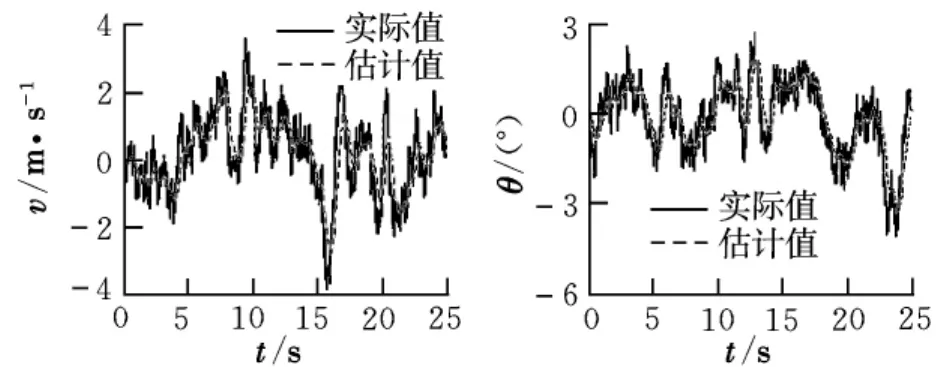
圖5 卡爾曼濾波對大氣紊流的估計

從圖5可以看出，卡爾曼濾波能實時跟蹤上大氣紊流的變化情況。圖6給出了大氣紊流對縱向運動的影響。

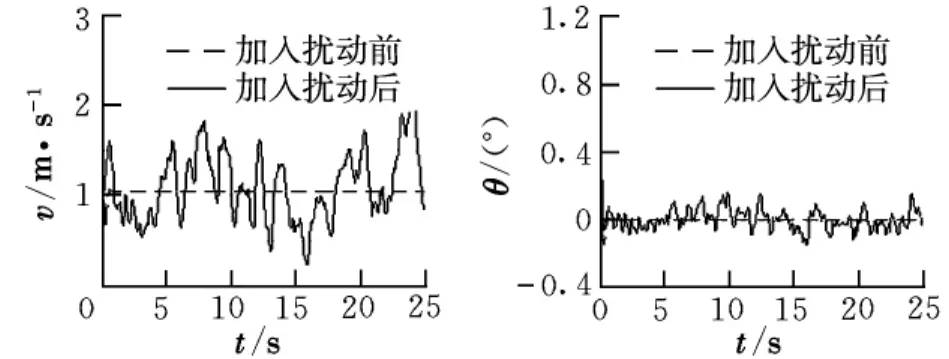
圖6 大氣紊流對縱向運動的影響

從圖6可以看出，大氣紊流使直升機偏離原來的平衡位置，本文提出的控制方法對俯仰角的控制效果良好，且穩態誤差在10%之內，而對縱向線速度的控制效果不是很理想。

4.2 橫向仿真

文獻［8］中給出了橫向運動方程中參數數值的大小，將其帶入式(2)后得到下列矩陣:

通過矩陣A求得橫向運動方程的零極點如圖7所示。

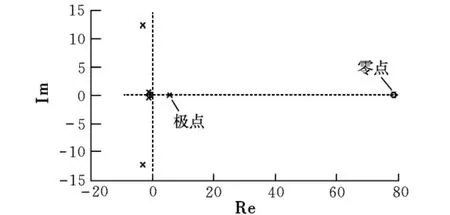
圖7 橫向運動方程的零極點圖

從圖7可以看出，有一個零點和一個極點位于s復平面的右半平面，說明系統是不穩定的。經過多次反復的試驗，得到LQR控制器中的q和r的參數取值如下:

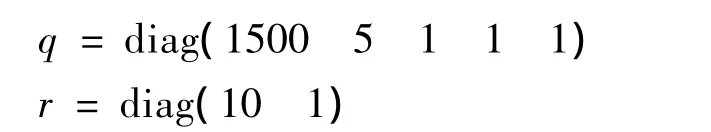
當直升機處于大氣紊流場中時，紊流的大小和方向是未知的，可由式(10)仿真得到。圖8給出了卡爾曼濾波對大氣紊流的估計結果。

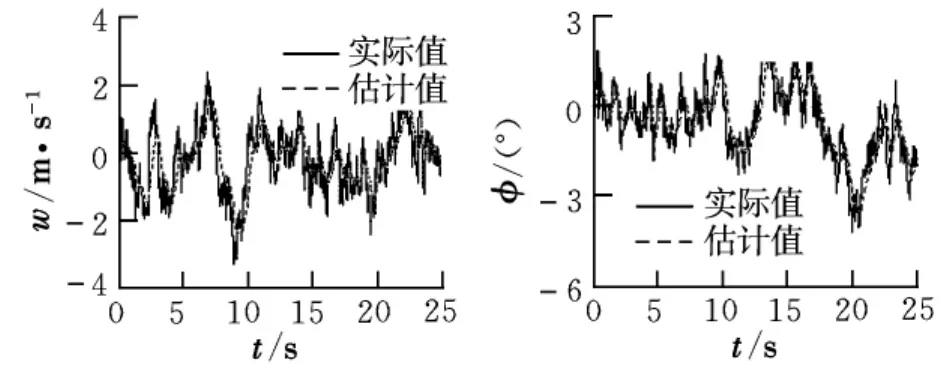
圖8 卡爾曼濾波對大氣紊流的估計

從圖8可以看出，卡爾曼濾波能實時跟蹤上大氣紊流的變化情況。圖9給出了大氣紊流對橫向運動的影響。

從圖9可以看出，大氣紊流使直升機偏離原來的平衡位置，本文提出的控制方法對橫向線速度的控制效果良好，且穩態誤差在5%之內，而對滾轉角的控制效果不是很理想。

5 結束語

針對大氣紊流環境下無人直升機飛行穩定性問題，提出了一種將主動建模技術與LQG控制相結合的控制算法。通過仿真實驗可以看出，該種控制方法中的卡爾曼濾波能夠實時跟蹤大氣紊流的變化情況，并且對大氣紊流有一定的抑制作用。該種控制方法的控制效果并不是十分理想，仍需要更深入的研究與思考。

［1］ 阮穎錚，田軍.飛行器翼身結合部的散射特性分析［J］.航空學報，1992，20(3):51-55.

［2］ 張文明，代冀陽，吳劍.采用LQR方法的縱列式直升機懸停控制與仿真［J］.微計算機信息(測控自動化)，2010，26(9):172-174.

［3］ 劉冰，艾劍良.基于LQG/LTR方法的飛機自動著陸系統設計［J］.動力學與控制學報，2010，8(1):92-96.

［4］ 姜哲，趙新剛，齊俊桐，等.基于主動建模的無人直升機增強LQR控制［J］.吉林大學學報(信息科學版)，2007，25(5):553-559.

［5］ 肖業倫，金長江.大氣擾動中的飛行原理［M］.北京:國防工業出版社，1993.

［6］ 汪沛，張峰，趙振鵬.飛行性能仿真中風場模型的研究［J］.微計算機信息(測控自動化)，2008，24(10):302-304.

［7］ 沈福生.小型無人直升機飛行力學參數化模型辨識研究［D］.南京:南京航空航天大學，2008.

［8］ Dalei Song，Juntong Qi，Lei Dai，et al.Modeling a smallsize unmanned helicopter using optimal estimation in the frequency domain［C］//15th International conference on Mechatronics and Machine Vision in Practice.Auckland，New-Zealand，2008:97-102.

［9］ 王文龍.大氣風場模型研究及應用［D］.長沙:國防科學技術大學，2009.