空空導(dǎo)彈高拋彈道作戰(zhàn)效能研究
崔垚,李順利,計佳俊,魏廣東,雷煒
(哈爾濱工業(yè)大學(xué)航天學(xué)院,黑龍江哈爾濱 150001)
引言
制空權(quán)對戰(zhàn)爭的勝負(fù)起著決定性的作用,世界各國都在大力開展空空導(dǎo)彈的研究工作。超視距作戰(zhàn)將成為制空權(quán)爭奪的關(guān)鍵技術(shù),為此各國都在爭相研制射程更遠(yuǎn)和精度更高的空空導(dǎo)彈。
中制導(dǎo)是導(dǎo)彈制導(dǎo)過程中控制時間最長的且對導(dǎo)彈射程影響最大的階段。一般來說,中制導(dǎo)在設(shè)計時要充分衡量能量耗散的問題,盡量減小能量的消耗,使導(dǎo)彈在中制導(dǎo)過程中達(dá)到盡量遠(yuǎn)距離并且在結(jié)束時能供給末制導(dǎo)盡量大的初始能量。研究表明,提高導(dǎo)彈的飛行高度能夠有效地增加射程。在初始階段,導(dǎo)彈高拋射入較高的空域,高空的大氣密度低,導(dǎo)彈所受空氣阻力減小,使得導(dǎo)彈能夠飛行更長的距離。同時,進(jìn)入末制導(dǎo)時具有一定勢能,在末端攻擊時有著一定的優(yōu)勢。
1 數(shù)學(xué)模型建立
1.1 導(dǎo)彈運(yùn)動模型
為了方便研究,將導(dǎo)彈簡化為質(zhì)點(diǎn),其運(yùn)動模型為:
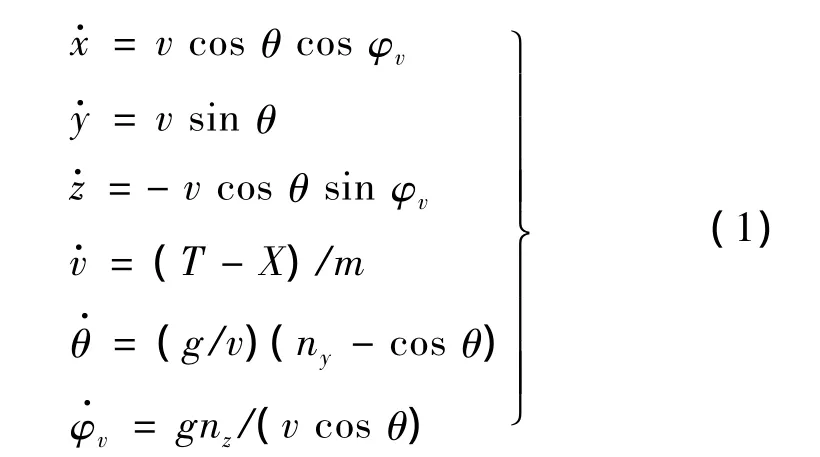
式中,(x,y,z)為導(dǎo)彈的坐標(biāo)位置;v為導(dǎo)彈的速度;θ為彈道傾角;φv為彈道偏角;ny,nz為縱向和側(cè)向過載控制量;T為發(fā)動機(jī)推力;X為空氣阻力。
1.2 目標(biāo)運(yùn)動模型
現(xiàn)代戰(zhàn)斗機(jī)在規(guī)避空空導(dǎo)彈攻擊時可做出多種機(jī)動飛行方式,本文選取四種典型機(jī)動飛行方式:水平面勻速直線運(yùn)動、水平面等過載等速轉(zhuǎn)彎、鉛垂面等過載爬升、等過載橫滾[1]。假設(shè)目標(biāo)最初在初始高度勻速直線飛行,當(dāng)彈目距離減少到30 km時,目標(biāo)開始機(jī)動飛行。
2 制導(dǎo)律設(shè)計
一般空空導(dǎo)彈的初制導(dǎo)時間較短,大多數(shù)為程序角控制,使導(dǎo)彈速度矢量在一定時間內(nèi)達(dá)到中制導(dǎo)導(dǎo)引要求。
2.1 奇異攝動中制導(dǎo)律
在中制導(dǎo)過程中,導(dǎo)彈將長時間處于巡航飛行。對此,可以將導(dǎo)彈看作是在兩種時間尺度內(nèi)工作:一種是由航向距離x、側(cè)向距離z、能量E和偏航角φv組成的慢變時間尺度系統(tǒng);一種是由高度y和彈道傾角θ組成的快變時間尺度系統(tǒng)。基于此分析,就可以應(yīng)用奇異攝動理論求解其最優(yōu)控制問題[2]。
本文把導(dǎo)彈的質(zhì)心運(yùn)動方程強(qiáng)迫用雙重時間尺度系統(tǒng)代替[3]:
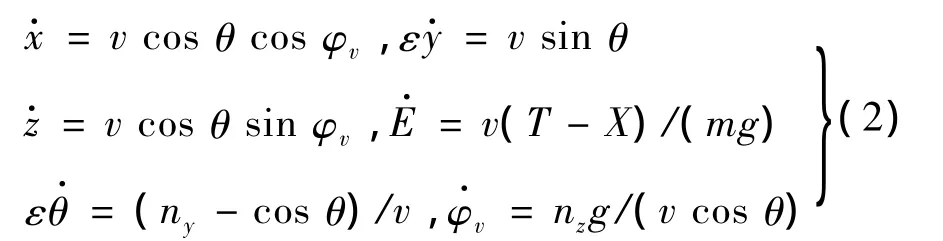
為了給末制導(dǎo)提供最大的初始速度,導(dǎo)彈在中制導(dǎo)階段盡量降低能量消耗。因此在推導(dǎo)過程中,取性能指標(biāo):
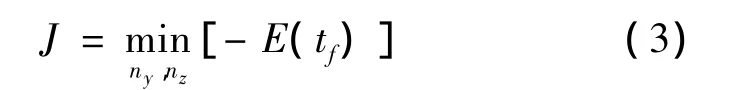
式中,tf為中制導(dǎo)結(jié)束時刻。
2.1.1 最小能量慢變控制器
對于式(2),令ε=0,得到降階后的子系統(tǒng)。
根據(jù)最優(yōu)控制理論推導(dǎo)得到:
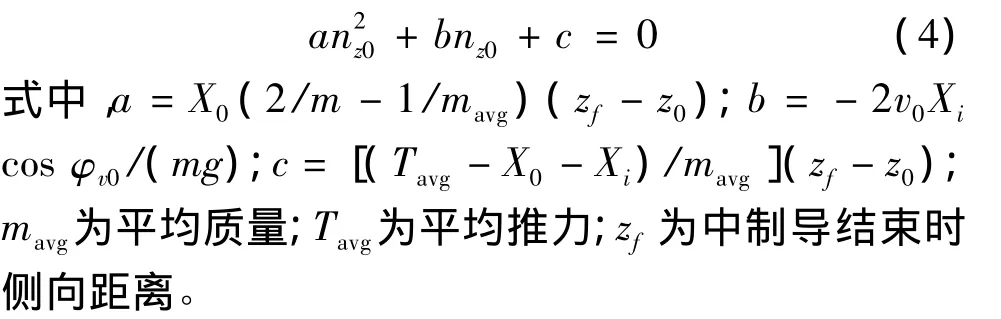
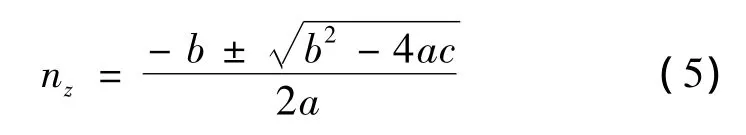
最小能量慢變控制器nz只需要載機(jī)為導(dǎo)彈提供中制導(dǎo)末端的側(cè)向位置zf便可。
2.1.2 快變控制器
快變控制器的設(shè)計就是要使導(dǎo)彈在中制導(dǎo)段初始時,快速向上大角度轉(zhuǎn)彎以最快的時間到達(dá)最優(yōu)高度轉(zhuǎn)入平飛;并且在中制導(dǎo)末段時使導(dǎo)彈下降,從而進(jìn)入可以對目標(biāo)進(jìn)行安全捕獲的區(qū)域。給中制導(dǎo)段一個光滑的彈道。應(yīng)用奇異攝動理論求解上述問題就是一個具有兩點(diǎn)約束問題的優(yōu)化過程。
取快變時間尺度τ1=(t-t1)/ε,代替原系統(tǒng)時間變量。取ε=0,有:

全階系統(tǒng)的狀態(tài)變量可直接應(yīng)用降階后系統(tǒng)狀態(tài)變量的對應(yīng)關(guān)系,因此受到的影響是很小的,于是得到如下的具有反饋形式的全階系統(tǒng)控制器nz:

受到這個快變控制器的作用,將促使快變狀態(tài)y,θ逐漸趨近于由慢變子系統(tǒng)決定的穩(wěn)定軌跡,即y→y0,θ→θ0,達(dá)到穩(wěn)定之后,導(dǎo)彈便可轉(zhuǎn)入最優(yōu)高度上的巡航飛行。
如果導(dǎo)彈一直在最優(yōu)高度上做巡航飛行,不能滿足中、末制導(dǎo)交接班的條件,還需要在右端邊界層(即中制導(dǎo)末段)加入控制量nyb。研究線性系統(tǒng)在右邊界層ω=ωF+ωS+ωb,V=VF+VS+Vb。根據(jù)奇異攝動相關(guān)理論可知:
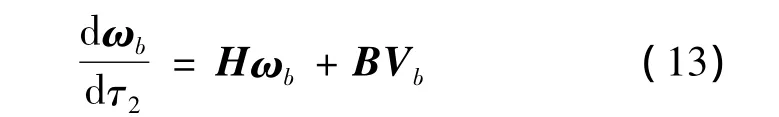
式中,H=A+BK';ωb和Vb分別為系統(tǒng)在右邊界層時的狀態(tài)量和控制量;τ2=(t-tf)/ε為該狀態(tài)此階段處于右邊界層內(nèi)。由最優(yōu)控制相關(guān)理論能找到最小能量控制器:

式中,yf,vf,θf分別為導(dǎo)彈在預(yù)測的中制導(dǎo)末端時刻tf處所應(yīng)到達(dá)的高度、速度和彈道傾角。可見,控制過載ny由三段組成:控制巡航段、控制爬升段和控制下滑段。
2.2 彈道形成最優(yōu)中制導(dǎo)律
彈道形成最優(yōu)中制導(dǎo)律是根據(jù)中制導(dǎo)的要求提出的,目的是使末速度最大。導(dǎo)彈在中間段的飛行過程中,火控系統(tǒng)通過雙向數(shù)據(jù)鏈可以為導(dǎo)彈定期提供目標(biāo)信息,根據(jù)目標(biāo)現(xiàn)在的速度、位置和加速度信息對目標(biāo)將來的機(jī)動情況做出基本的預(yù)測,然后根據(jù)這個預(yù)測信息,形成彈道指令控制導(dǎo)彈朝向這個預(yù)測的攔截點(diǎn)飛行。將導(dǎo)彈送到最后的中末制導(dǎo)交接點(diǎn)上。
彈道形成最優(yōu)中制導(dǎo)律的基本形式[4]為:
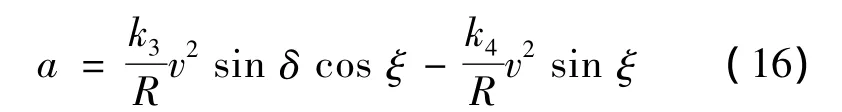
式中,R為導(dǎo)彈到預(yù)測交接點(diǎn)的間距;δ為導(dǎo)彈的速度矢量v和導(dǎo)彈預(yù)定的末速度矢量之間所成的角度;ξ為速度矢量v與導(dǎo)彈到預(yù)測交接點(diǎn)G連線之間所成的角度;k3和k4分別為對應(yīng)項的系數(shù)。把式(16)分解到縱向平面和側(cè)向平面,并利用最優(yōu)控制理論尋找優(yōu)化的和以滿足末速最大的性能指標(biāo)[5]:
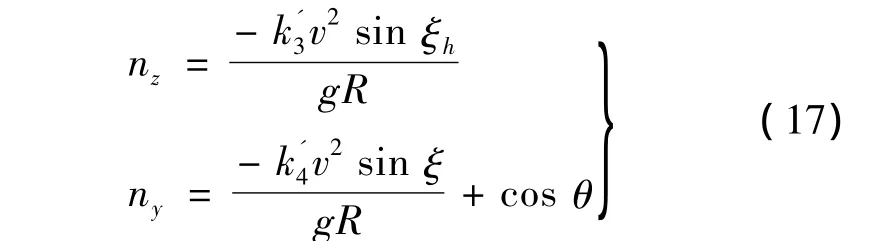
2.3 三維比例制導(dǎo)律
廣義比例導(dǎo)引的俯仰偏航控制方程為:
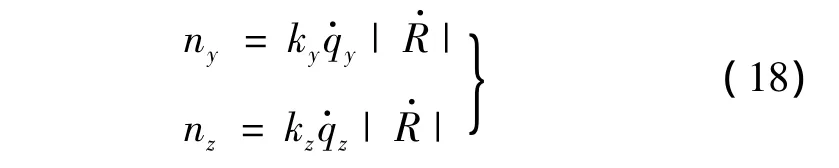
式中,ky,kz為比例導(dǎo)引系數(shù)分別為彈目視線角變化率在縱向平面和橫向平面的投影;為彈目距離變化率。
2.4 中末制導(dǎo)交接班
為了使導(dǎo)彈在中末制導(dǎo)交接班順利完成,在中末制導(dǎo)引入系數(shù)K。這樣,過載在交接點(diǎn)附近能夠平滑過渡[6],表達(dá)式為:
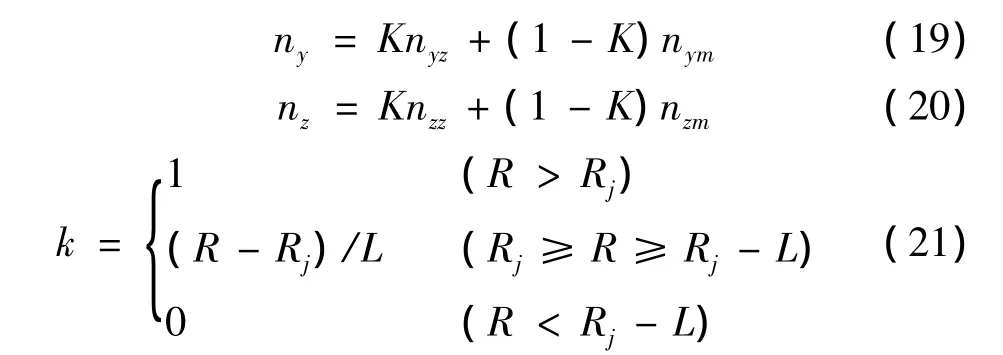
式中,Rj為中末制導(dǎo)交接班距離;L為交接班過程距離。
3 仿真分析
為了考察奇異攝動中制導(dǎo)律的增程效果,本文以導(dǎo)彈進(jìn)入中制導(dǎo)時彈目航向(x軸)初始距離為空空導(dǎo)彈武器系統(tǒng)效能的衡量指標(biāo)(以下稱攻擊距離)。對四種不同目標(biāo)機(jī)動方式進(jìn)行彈道仿真,通過設(shè)置不同初始距離,利用二分法分別求得導(dǎo)彈對目標(biāo)四種機(jī)動方式最遠(yuǎn)攻擊距離,選取四個結(jié)果中的最小值作為該制導(dǎo)模式下的最遠(yuǎn)攻擊距離。
在設(shè)計仿真程序時,首先建立腳本文件,利用Matlab語言編程設(shè)置導(dǎo)彈和目標(biāo)的初始高度,并采用二分法計算目標(biāo)航向初始距離,調(diào)用Simulink建立的彈道模型解算彈道,求得所設(shè)定高度下的最遠(yuǎn)初始攻擊距離。仿真程序流程如圖1所示。
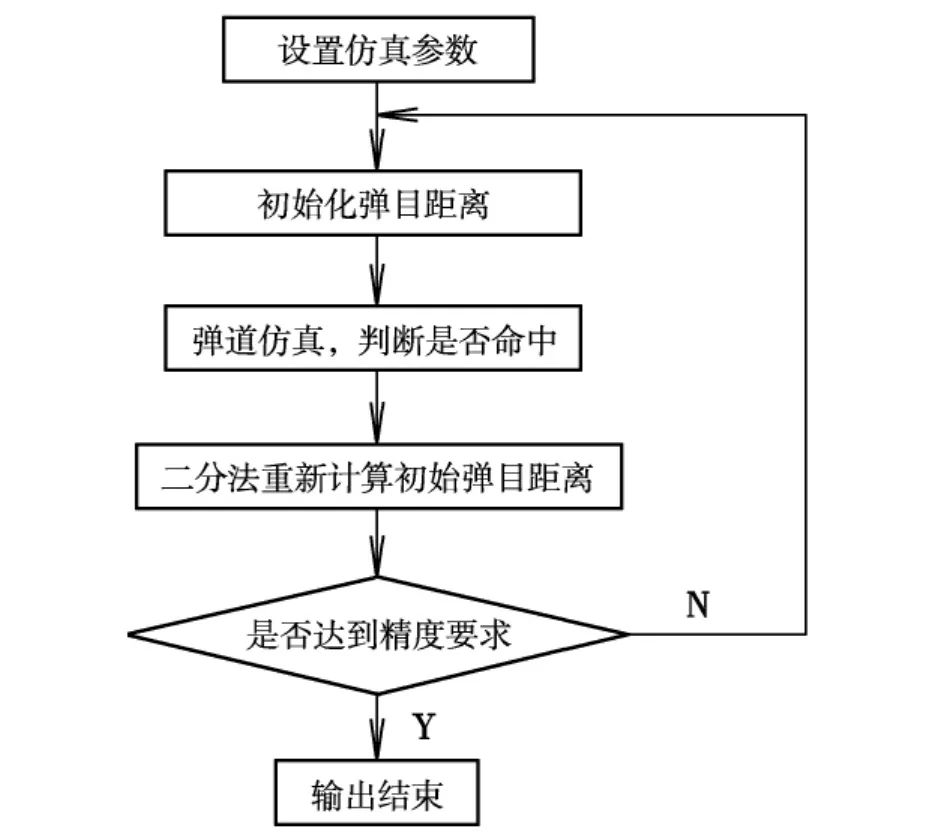
圖1 仿真程序流程圖
命中條件:(1)導(dǎo)彈飛行時間小于導(dǎo)彈設(shè)計工作時間;(2)脫靶量小于或等于導(dǎo)彈殺傷半徑。
為研究高拋彈道在提升導(dǎo)彈作戰(zhàn)效能方面的適用性,本文選取五種情況將其與常規(guī)彈道進(jìn)行仿真對比,仿真結(jié)果如圖2~圖6所示(hM為導(dǎo)彈初始高度,hT為目標(biāo)初始高度,s為攻擊距離)。
(1)導(dǎo)彈與目標(biāo)初始位置在同一高度。
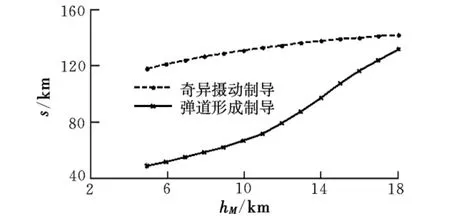
圖2 彈目初始等高時攻擊距離曲線
(2)初始時刻目標(biāo)位于導(dǎo)彈上方3 km。
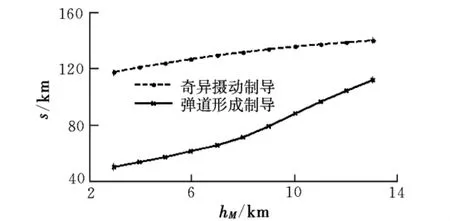
圖3 目標(biāo)初始在導(dǎo)彈上方時攻擊距離曲線
(3)初始時刻目標(biāo)位于導(dǎo)彈下方3 km。
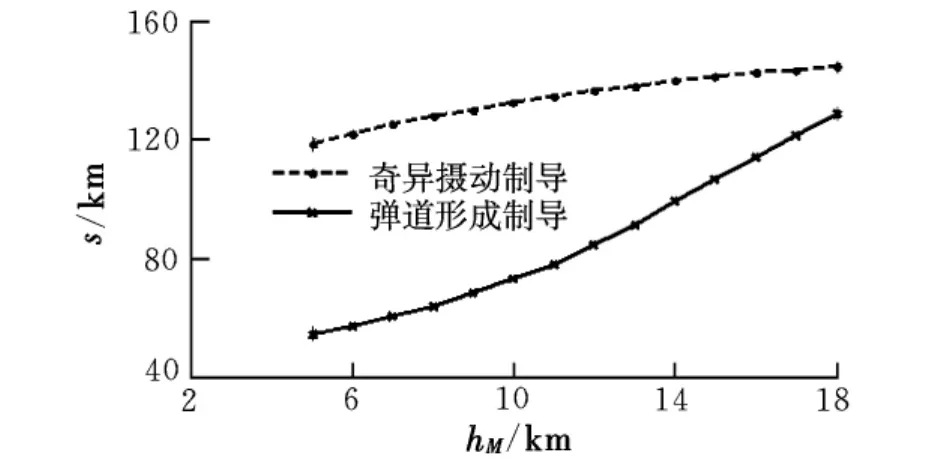
圖4 目標(biāo)初始在導(dǎo)彈下方時攻擊距離曲線
(4)導(dǎo)彈初始高度10 km,目標(biāo)高度從5 km到18 km。
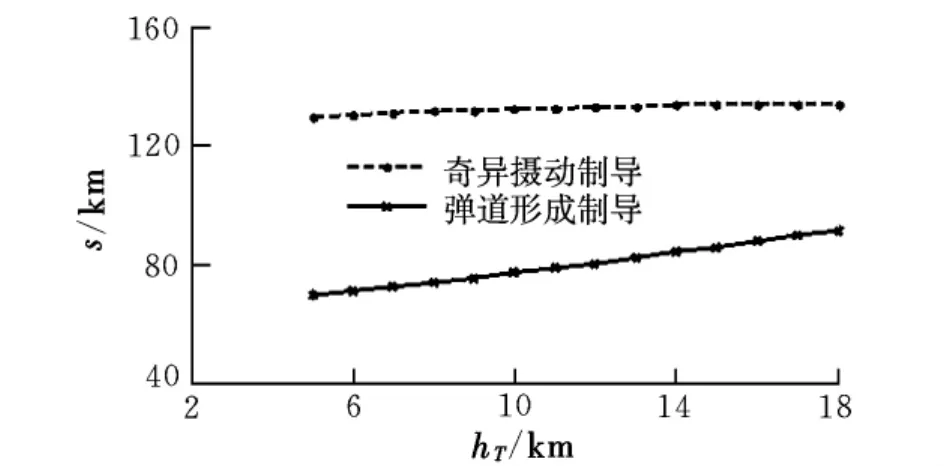
圖5 導(dǎo)彈初始高度10 km攻擊距離曲線
(5)目標(biāo)初始高度10 km,導(dǎo)彈高度從5 km到18 km。
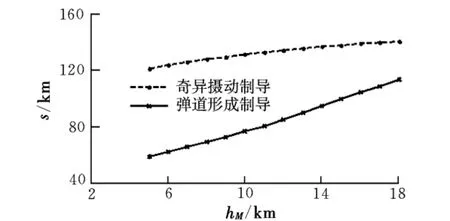
圖6 目標(biāo)初始高度10 km攻擊距離曲線
由圖可知,奇異攝動制導(dǎo)律利用空氣密度隨高度的增加而減小的性質(zhì),找到飛行的最佳高度,使得導(dǎo)彈在進(jìn)入末制導(dǎo)時具有速度和能量上的優(yōu)勢,從而增大導(dǎo)彈的射程。高拋彈道在初始彈目高度較低的情況下優(yōu)勢明顯,隨著高度的增加,采用高拋彈道的作戰(zhàn)優(yōu)勢逐漸下降。當(dāng)初始時刻彈目之間存在高度差時,導(dǎo)彈的初始作戰(zhàn)高度和彈目相對位置不影響高拋彈道的攻擊距離,對于常規(guī)彈道來說,攻擊距離隨作戰(zhàn)高度的提升而增加。當(dāng)導(dǎo)彈初始高度一定時,兩種彈道的攻擊距離基本不隨目標(biāo)高度變化而變化,因?yàn)殡S著目標(biāo)高度增加,大氣密度變小,導(dǎo)彈所受到的空氣阻力隨之減小,飛行速度增大,彌補(bǔ)了初始高度差對攻擊距離的影響。當(dāng)目標(biāo)高度一定時,常規(guī)導(dǎo)彈的攻擊距離隨著導(dǎo)彈的初始高度大幅提升,說明導(dǎo)彈的初始飛行高度對常規(guī)導(dǎo)彈攻擊距離影響較大。而高拋彈道的攻擊距離基本不隨作戰(zhàn)高度變化,其主要影響因素是導(dǎo)彈工作時間。
4 結(jié)束語
本文針對遠(yuǎn)程空空導(dǎo)彈的特點(diǎn),為達(dá)到增程的目的,提出了利用奇異攝動方法實(shí)現(xiàn)讓導(dǎo)彈迅速爬升并在最優(yōu)高度上巡航飛行,從而形成高拋彈道,通過彈道仿真,得到了不同初始高度條件下高拋彈道的性能特點(diǎn)。結(jié)果顯示,奇異攝動制導(dǎo)可以節(jié)省能量,增加射程,有效地提高了遠(yuǎn)程空空導(dǎo)彈的作戰(zhàn)效能,但隨著作戰(zhàn)高度的增加,高拋彈道的射程優(yōu)勢逐漸減小。
奇異攝動中制導(dǎo)雖然可以有效地提高導(dǎo)彈的射程,但長時間高空飛行增加了導(dǎo)彈與載機(jī)之間數(shù)據(jù)交換的難度。同時,導(dǎo)彈長時間沒有指向目標(biāo),這對末制導(dǎo)目標(biāo)捕獲時的敏感度提出了更高要求,需要在今后設(shè)計出更有效的中末制導(dǎo)交接班算法。
[1] 楊超.中程空空導(dǎo)彈效能研究[D].西安:西北工業(yè)大學(xué),2007.
[2] 喬洋,陳剛,陳士櫓,等.一種快速爬升和快速下降的奇異攝動最優(yōu)中制導(dǎo)律設(shè)計[J].固體火箭技術(shù),2008,31(3):205-224.
[3] Van Buren A,Mease K D.Aerospace plan guidance using timescale decomposition and feedback linearization[J].Journal of Guidance,1992,15(5):1166-1174.
[4] Lin C F,Tsai L L.Analytical solution of optimal trajectoryshaping guidance[J].Journal of Guidance,1987,10(1):61-66.
[5] 王冠軍.中遠(yuǎn)程空空導(dǎo)彈復(fù)合制導(dǎo)研究[D].西安:西北工業(yè)大學(xué),2004.
[6] 楊雪榕,梁加紅,李曉冬.空空導(dǎo)彈高拋彈道仿真研究[J].系統(tǒng)仿真學(xué)報,2010,22(5):1261-1265.

